2025.10.17

記事内に商品プロモーションを含む場合があります

ループ回数の求め方：全探索・組合せ・重複組合せの3パターンを解説

Aru

アルゴリズムでは、ループが「何回まわるか」を把握することがしばしば重要になります。本記事では、ループ構造の典型的な３つのパターンについて、それぞれのループ回数の計算の仕方を図を使ってわかりやすく解説します。

Contents

ループの回数を求める

以下、３つのパターンについてループ回数を求めてみます。

１つ目は、全てのループが0~N-1回の場合の例です。それぞれのループはN回ずつループするので、ループ回数はN*N*N...になります。

ループの深さを$k$と置くと、合計ループ回数は以下のように表すことができます。

$$
\prod_{i=1}^k N
$$

以下はk=3の例です。

N = 10
cnt = 0
for i0 in range(N):
  for i1 in range(N):
    for i2 in range(N):
      cnt+=1
print(cnt)

$N^3 = 1000$で、プログラムの出力は1000と一致します。

i0が0の時、i1が1~となるような場合になります。

k=3のときを例にすると以下のようなプログラムになります。

N = 10
cnt = 0
for i0 in range(N):
  for i1 in range(i0+1, N):
    for i2 in range(i1+1, N):
      cnt+=1
print(cnt)

この場合の考え方ですが、0<=i0<i1<i2<Nとなるi0, i1, i2の組合せを考えるのと同じになるので、「n個からk個を選択する」場合の数と一致します。つまり、$_nC_k$となります。

$$
_nC_k
$$

図で見ると以下のようなイメージになります。図では、i0=0, i1=2, i2=6の例です。条件i0<i1<i2からi0,i1,i2は同じ値になりません。また、i0はi1, i2より小さい値となるので選んだk個に小さい値からi0, i1, ...と割り当てたのと一致します。

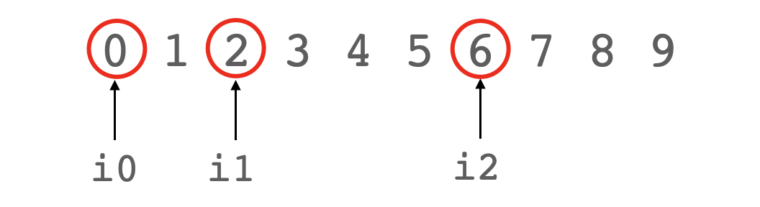
実際に、上記のプログラムを実行した結果は120で、$_{10}C_3 = 120$と一致します

先ほどの場合と異なるのはi0=i1などの「同値」があることです。

同じ値を許すこのループのループ回数は、重複組合せの数と一致します。

$$
_nH_k = _{n+k-1}C_k
$$

N = 10
cnt = 0
for i0 in range(N):
  for i1 in range(i0, N):
    for i2 in range(i1, N):
      cnt+=1
print(cnt)

これは、図で考えた方がわかりやすいです。下図はi0=1,i1=2,i2=5の例です。重複組み合わせは、区切りで示したが方がわかりやすいので赤線で示しています。

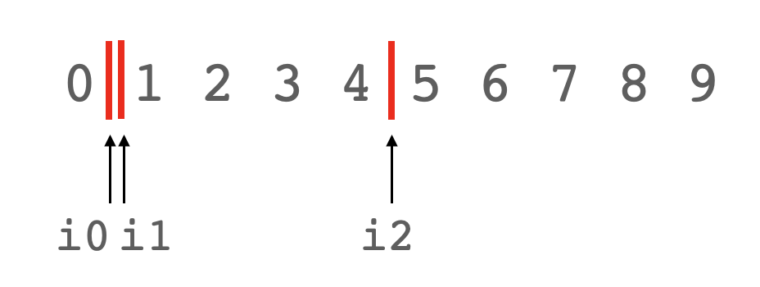
実際にプログラムを実行すると220で、$_{10+3-1}C_3=220$と計算結果と一致します。

重複組合せについては以下の記事も参考にしてください。

ループ回数について解説しました。計算量の見積もりでは$O(N^k)$となりますが、実際のループ回数が知りたい場合は覚えて置くと便利です。