パスカルの三角形を使った組み合わせ数の計算方法｜Python

Aru

競技プログラミングでは、「組み合わせ数（コンビネーション, nCr）をMで割った余りを計算」する問題がたまに出題されます。多くの場合Mは素数なことが多いですが、素数でない場合は厄介です。ここでは、パスカルの三角形を使ってnCrを計算する方法を紹介します。

Contents

nCrをMで割ったあまりの計算
- Mが素数の場合
- Mが素数でない場合
パスカルの三角形
パスカルの三角形を使ってnCrを計算するPythonクラス
- nCrクラス
- 使い方
まとめ

nCrをMで割ったあまりの計算

Mが素数の場合

Mが素数の場合は、逆元（1/M）が簡単に計算できるので、

$$
_nC_r = \frac{n!}{r!(n-r)!}
$$

の計算をそのまますることができます。具体的には、$n!$, $r!$, $(n-r)!$を計算して、$1/r!$, $1/(n-r)!$をフェルマーの小定理を利用して計算し、掛け合わせればOKです。

Mが素数でない場合

Mが素数でない場合はフェルマーの小定理を利用した逆元の計算ができないため、面倒になります。この場合は、他のアプローチが必要になります。

ここでは、パスカルの三角形を使った解法を解説します。

パスカルの三角形

パスカルの三角形って？

パスカルの三角形は、二項展開における二項係数を三角形に並べたものです。具体的には以下のようなものになります。

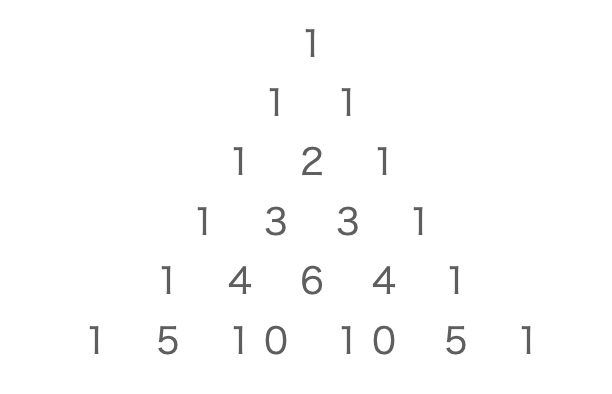
これは、以下のように$_nC_r$に対応します。

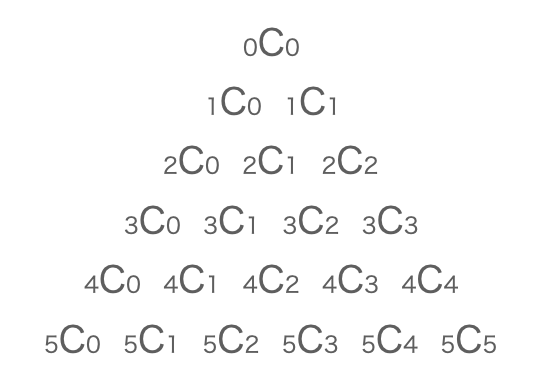
また、パスカルの三角形は、上から左右の値を足した結果をくりかえした構造になっていて、頂点から順番に計算することが可能です。

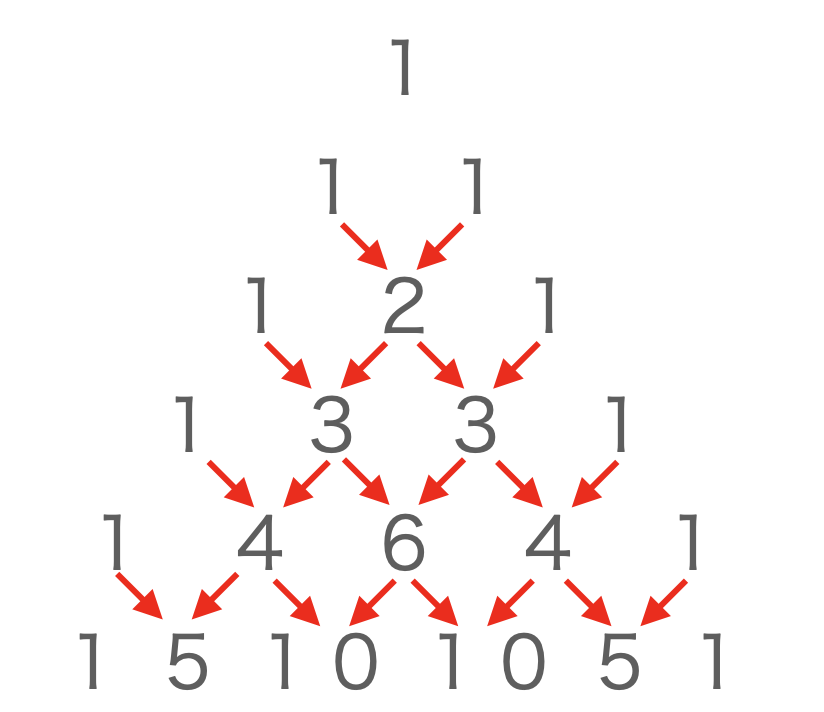
配列に格納する

多少無駄になりますが、これをNxNの配列Cに格納することを考えます。左詰で考えると以下のようになります。

index	0	1	2	3	4	5
0	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1

このように配置するとC[n][r]が$_nC_r$の値を格納するので扱いやすいです。

どのくらいのサイズまでOKか？

仮にN=1,000とします。するとN^2 = 1,000,000となります。64bit（8byte）の整数だと、これは8Mbyteに相当します。計算回数は10^6です。AtCoderのABCの制約をみるとメモリが1024MBまでOKなのでまだまだ行けそうです。

N=10,000とすると、N^2=100,000,000となりメモリはギリギリ大丈夫そうですが、計算回数が10^8となり少し厳しくなります。

実際に使えるのはN<10,000以下だと考えた方が良いかと思います。

パスカルの三角形を使ってnCrを計算するPythonクラス

nCrクラス

class nCr :
    def __init__(self, n, mod) :
        self.c = [[0 for _ in range(n)] for _ in range(n)]
        self.c[0][0] = 1
        for i in range(n-1) :
            for j in range(i+1) :
                self.c[i+1][j] += self.c[i][j]
                self.c[i+1][j] %= mod
                self.c[i+1][j+1] += self.c[i][j]
                self.c[i+1][j+1] %= mod

    def nCr(self, n, r) :
        return self.c[n][r]

使い方

クラスは以下のように使います。
今回作成したクラスでは、[0, n)までのテーブルを作成するので、$_5C_i$を計算したい場合は、nCr(6, mod)とすることに注意してください。

n = 5
mod = 100
c = nCr(n+1, mod)
for i in range(n+1) :
    for j in range(i+1) :
        print(f"{i}C{j} = ", end="")
        print(c.nCr(i, j), end=" ")
    print()

結果は以下のようになります

実行結果

0C0 = 1 
1C0 = 1 1C1 = 1 
2C0 = 1 2C1 = 2 2C2 = 1 
3C0 = 1 3C1 = 3 3C2 = 3 3C3 = 1 
4C0 = 1 4C1 = 4 4C2 = 6 4C3 = 4 4C4 = 1 
5C0 = 1 5C1 = 5 5C2 = 10 5C3 = 10 5C4 = 5 5C5 = 1

ちなみにmod=10とすると以下のように10以上の部分が正しく変化します。

実行結果

0C0 = 1 
1C0 = 1 1C1 = 1 
2C0 = 1 2C1 = 2 2C2 = 1 
3C0 = 1 3C1 = 3 3C2 = 3 3C3 = 1 
4C0 = 1 4C1 = 4 4C2 = 6 4C3 = 4 4C4 = 1 
5C0 = 1 5C1 = 5 5C2 = 0 5C3 = 0 5C4 = 5 5C5 = 1