MENU
プログラミング
記事内に商品プロモーションを含む場合があります

【Python】二分探索の実用例｜積立投資の必要年利を逆算するプログラム

Aru

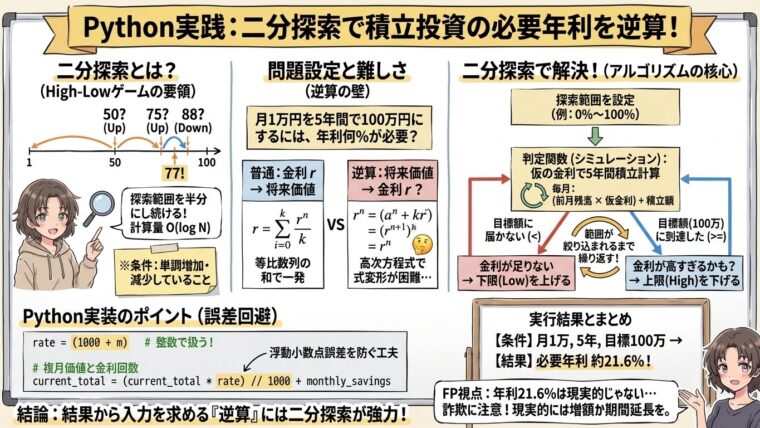
競技プログラミングやアルゴリズムの学習で必ず登場する「二分探索（Binary Search）」。 「ソート済み配列から値を探索する」という例題が有名ですが、実務や実生活での使いどころがイメージしづらいという方も多いのではないでしょうか。

実は二分探索は、「答えから入力を逆算する」というシーンで非常に強力なツールとなります。

今回は、技術者×FP（ファイナンシャルプランナー）の視点から、「積立投資で目標額に到達するために必要な年利」を二分探索を二分探索の実用例として紹介します。

Contents
  1. 二分探索とは？
  2. 問題設定：5年で100万円貯めるには？
  3. まとめ

二分探索とは？

二分探索（Binary Search）とは、「ソート済み（整列済み）」のデータ群から、特定の値を高速に見つけ出すアルゴリズムです。

イメージしやすい例として、「辞書で単語を引くとき」や「数当てゲーム（High-Lowゲーム）」がよく挙げられます。

例えば、1〜100の数字の中から正解の数字（例えば77）を当てるゲームを想像してください。 「1から順に聞いていく（線形探索）」と最大100回質問する必要がありますが、二分探索なら以下のように効率よく絞り込めます。

  1. 全体の真ん中である「50」ですか？ $\rightarrow$ もっと上です（範囲が51〜100に半減）
  2. 残りの真ん中である「75」ですか？ $\rightarrow$ もっと上です（範囲が76〜100に半減）
  3. 残りの真ん中である「88」ですか？ $\rightarrow$ もっと下です（範囲が76〜87に半減） …

このように、「範囲の真ん中を見て、探索範囲を半分に絞る」ことを繰り返すため、データ量が倍になっても計算回数は1回しか増えません。この効率の良さ（計算量 $O(\log N)$）が最大の特徴です。

二分探索が利用できる条件は、「単調減少または、単調増加」という規則があることです。先ほど例だと、1~100の数字の並びは単調増加です。

プログラム的には、下限（Low）と上限（High）を設定して、その中間の値（mid = (High – Low)/2）を試してみて、判定結果により[Low:mid]または、[mid:High]の区間に絞り込んでいくものです。

問題設定：5年で100万円貯めるには？

今回解く問題は以下の通りです。

問題

「毎月1万円を積み立てて、5年間で100万円にするには、年利何%での運用が必要か？」

通常、積立計算には等比数列の和の公式などが使われますが、最終的な金額から利率 $r$ を逆算するのは方程式が複雑になりがちです。 そこで、コンピュータの計算力を活かして、二分探索で近似解を求めてみます。

「毎月1万円を年利r%で5年積み立てたらいくらになるか（将来価値）」を求める計算は、等比数列の和の公式を使って一発で計算できます。しかし、今回のように「いくらになるか（目標額）から年利を逆算する」場合、方程式が高次（$r^n$が含まれる形）になるため、単純な式変形（$r = \dots$ の形）では解けません。そのため、今回紹介する二分探索のような数値計算手法が役立つのです。

アルゴリズムの考え方

先ほども言ったように、二分探索が適用できる最大の条件は、対象に「単調性」がある場合です。 今回のケースは、以下のように単調性が成立しています。

  • 年利が上がる $\rightarrow$ 5年後の積立総額も増える
  • 年利が下がる $\rightarrow$ 5年後の積立総額も減る

この性質を利用して、以下のようなアプローチをとります。

  1. 判定関数を用意する：ある年利 $X$ % のとき、5年後にいくらになるかを計算する。
  2. 範囲を決める：年利 0% 〜 100%（あるいはそれ以上）を探索範囲とする。
  3. 範囲を絞る：
    • 計算結果 < 目標額 なら、もっと利率が必要 $\rightarrow$ 下限を上げる（l = m）
    • 計算結果 $\geqq$ 目標額 なら、利率が高すぎたかも $\rightarrow$ 上限を下げる（r = m）

これを繰り返すことで、目標金額ギリギリに到達する利率を特定します。

ソースコード

以下がPythonによる実装例です。 浮動小数点の誤差を回避するため、内部計算では利率を整数（1000倍スケール）として扱っています。

def calc(months, monthly_savings, target_amount):
    """
    二分探索を用いて目標金額に到達するために必要な年利を計算する
    
    Args:
        months (int): 積立期間（月数）
        monthly_savings (int): 毎月の積立額（円）
        target_amount (int): 目標金額（円）
        
    Returns:
        float: 必要な年利（%）
    """
    # 探索範囲の設定（月利ベースの係数として扱う）
    # l, r は「月利 0.1%」単位の整数として扱う（例: 10 => 月利1%）
    l, r = -1, 1000  # -0.1% 〜 100% (月利) 程度の広い範囲をとる
    
    # 二分探索開始
    while l + 1 != r:
        m = (l + r) // 2
        
        # その利率(m)でシミュレーションを行う
        current_total = 0
        for _ in range(months):
            # 1000をベースに m を足すことで擬似的に利率を表現
            # m=10 の場合、rate=1010 となり 1.01倍（月利1%）を意味する
            rate = (1000 + m)
            # (現在の額 * 利率) + 今月の積立額
            current_total = (current_total * rate) // 1000 + monthly_savings
        
        # 判定: 目標額に届いたか？
        if current_total >= target_amount:
            r = m  # 届いたなら、もっと低い利率でもいける -> 上限を下げる
        else:
            l = m  # 届かないなら、もっと高い利率が必要 -> 下限を上げる

    # 結果の変換
    # m は「月利の0.1%単位」なので、12倍して年利にし、0.1%単位を%に戻すために10で割る
    # 式: m * 12 / 10
    return r * 12 / 10

# --- メイン処理 ---

if __name__ == "__main__":
    # 条件設定
    years = 5
    monthly_savings = 10_000
    target_amount = 1_000_000

    # 月数に変換
    n_months = years * 12

    # 計算実行
    required_annual_rate = calc(n_months, monthly_savings, target_amount)

    print(f"【条件】")
    print(f"・毎月積立: {monthly_savings:,} 円")
    print(f"・期間: {years} 年 ({n_months}ヶ月)")
    print(f"・目標額: {target_amount:,} 円")
    print("-" * 30)
    print(f"必要な年利は... 約 {required_annual_rate:.1f} % です！")

このコードのポイントは、「浮動小数点誤差を避けるために整数だけで計算している」点です。

金融計算では、小数の誤差が積み重なると無視できないズレになることがあるため、工夫しています。

  1. 利率の表現（整数化）
    通常、計算では 1.05 などの小数を使いますが、ここでは 1000 を基準（1.00倍）とし、それに整数 m を足すことで利率を表現しています。
  2. シミュレーション（内部ループ）
    仮定した利率 m を使って、指定期間（months）の積立シミュレーションを行います。 current_total = (current_total * rate) // 1000 + monthly_savings この式は、「前月までの合計に利息を乗せ（//1000で元のスケールに戻す）、今月の積立額を足す」という複利計算を行っています。
  3. 探索範囲の更新
    探索範囲は、現在のrate（1000+m)の利率で計算した結果により区間を小さくしていきます。
    • 計算結果が目標額以上（current_total >= target_amount）の場合はその利率で達成可能です。「もっと低い利率でもいけるかも？」と判断し、探索範囲の上限を下げます（r = m）。
    • 計算結果が目標額未満の場合： 利率が足りません。「もっと高い利率が必要」と判断し、探索範囲の下限を上げます（l = m）。
  4. 結果の出力
    計算した結果出力されるのは「月利」なので12倍して「年利」に変換しています。

最終的に収束した r が、目標達成に必要なギリギリの利率となります。

実行結果

上記のコードを実行すると、以下の結果が得られます。

【条件】
・毎月積立: 10,000 円
・期間: 5 年 (60ヶ月)
・目標額: 1,000,000 円
------------------------------
必要な年利は... 約 20.4 % です！

計算の結果、年利 約20.4% が必要であることがわかりました。

参考：技術者的な考察

金融系の計算では誤差を嫌うので、今回は1000倍して整数値で処理を行うようにしています。今回は「ざっくりとした値」を知りたいだけなので、浮動小数点で行っても良いですが、金融系のプログラミングでは誤差は要注意です。

参考：ファイナンシャルプランナー的な考察

「年利20.4%」という数字が出ましたが、現代の低金利環境において、リスクを抑えつつこの利回りを5年間安定して出し続ける金融商品はまず存在しません。

このように数値を逆算してみると、「毎月1万円の積立で5年で100万円を作るのは現実的ではない（詐欺的な投資話には注意が必要）」ということが客観的に分かります。 現実的な解としては、積立額を増やすか、期間を10年〜15年に延ばすといった調整が必要になるでしょう。

まとめ

今回は、二分探索を使って金融計算（利率の逆算）を行う方法を紹介しました。

  • 入力から出力を求めるのがシミュレーション
  • 出力から入力を求めるのが二分探索（最適化手法）

このように捉えると、アルゴリズムの活用の幅がぐっと広がります。 「結果はわかるけど、式変形が難しい」という問題に出会ったときは、ぜひ二分探索のアプローチを試してみてください。

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

ABOUT ME
ある/Aru
ある/Aru
IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)
Contact
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
Recommend
こちらの記事もどうぞ
記事URLをコピーしました