ヴァンデルモンドの畳み込みと二項定理の関係

Aru

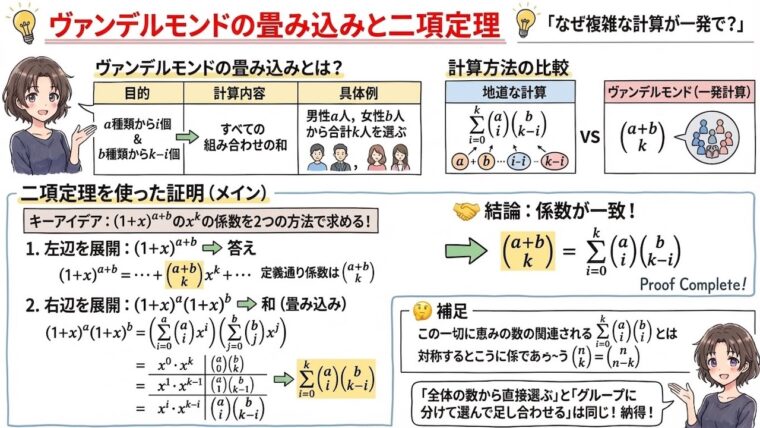
ヴァンデルモンドの畳み込みがどうも納得できなかったので、調べてみました。ヴァンデルモンドの畳み込みは、AとBからそれぞれi個ずつ取り出すときのiを0~kまで行った場合の総和を計算するのに便利な公式です。

Contents

はじめに
ヴァンデルモンドの畳み込みの証明
最初の問題に戻る
まとめ

はじめに

「男性a人と女性b人」で$i=0..k$人の組み合わせの通り数というのを計算しようとすると、男女一人づつ、二人づつ、…といった組み合わせの総和になるので、以下の式で計算することができます。

$$
\sum_{i=0}^k{
\begin{pmatrix}a\\i\end{pmatrix}
\begin{pmatrix}b\\i\end{pmatrix}
}
$$

つまり、すべての組み合わせについて計算して、総和を求める必要があります。これを、ヴァンデルモンドの畳み込みを使うと以下の計算一発で済みます。

$$
\begin{pmatrix}a+b\\k\end{pmatrix}
$$

どうしても納得がいかなかったので調べつつ、自前で証明してみました。証明方法はいくつかあるみたいですが、二項定理をつかうのが一番簡単みたいです。

ヴァンデルモンドの畳み込みの証明

二項定理

二項定理の式は、以下の通り

$$(a+b)^n = \sum_{i = 0}^{n}{
\begin{pmatrix}x\\y\end{pmatrix}
a^{n-i}b^i}$$

ヴァンデルモンドの畳み込み

ヴァンデルモンドの畳み込みは、以下の式です。

$$
\begin{pmatrix}a+b\\k\end{pmatrix} =
\sum_i{
\begin{pmatrix}a\\k\end{pmatrix}
\begin{pmatrix}b\\k-i\end{pmatrix}
}
$$

$(1+x)^{a+b} = (1+x)^a (1+x)^b$から

二項定理を使って証明する方法は、以下の通りです。まず、$(1+x)^{a+b}$を考えます。これは、以下のように変形することができます。

$$
(1+x)^{a+b} = (1+x)^a (1+x)^b
$$

左辺を二項定理により展開すると、

$$
(1+x)^{a+b} =
\begin{pmatrix}a+b\\0\end{pmatrix} x^0+
\begin{pmatrix}a+b\\1\end{pmatrix} x^1+ \cdots
\begin{pmatrix}a+b\\k\end{pmatrix} x^k+ \cdots
\begin{pmatrix}a+b\\a+b\end{pmatrix} x^{a+b}
$$

同様に右辺をそれぞれ展開すると、

$$
(1+x)^{a} =
\begin{pmatrix}a\\0\end{pmatrix} x^0+
\begin{pmatrix}a\\1\end{pmatrix} x^1+ \cdots
\begin{pmatrix}a\\k\end{pmatrix} x^k+ \cdots
$$

$$
(1+x)^{b} =
\begin{pmatrix}b\\0\end{pmatrix} x^0+
\begin{pmatrix}b\\1\end{pmatrix} x^1+ \cdots
\begin{pmatrix}b\\k\end{pmatrix} x^k+ \cdots
$$

$x_k$の項について考える

この中で$(1+x)^{a}(1+x)^{b}$が$x_k$となる組み合わせを考えます。すると、$x^0 x^k$, $x^1 x^{k-1}$…というくみ合わせが、$x_k$となることがわかります。

つまり、以下の組み合わせが$x^k$の係数です。

$$
\begin{pmatrix}a\\i\end{pmatrix}
\begin{pmatrix}b\\k-i\end{pmatrix}
$$

これをすべて合計したものが、

$$
\sum_{i=0}^k{
\begin{pmatrix}a\\i\end{pmatrix}
\begin{pmatrix}b\\k-i\end{pmatrix}
}
$$

となります。これが、$(1+x)^{a+b}$の$x^k$の係数と一致するので、結果として、

$$
\begin{pmatrix}a+b\\k\end{pmatrix} =
\sum_{i=0}^k{
\begin{pmatrix}a\\i\end{pmatrix}
\begin{pmatrix}b\\k-i\end{pmatrix}
}
$$

が成り立ちます。

最初の問題に戻る

疑問に思った人もいるかもしれません。
ヴァンデルモンドの畳み込みは、以下の式です。
$$
\begin{pmatrix}a+b\\k\end{pmatrix} =
\sum_i{
\begin{pmatrix}a\\k\end{pmatrix}
\begin{pmatrix}b\\k-i\end{pmatrix}
}
$$

一方、「男性a人と女性b人」の問題は以下の式です。

$$
\sum_{i=0}^k{
\begin{pmatrix}a\\i\end{pmatrix}
\begin{pmatrix}b\\i\end{pmatrix}
}
$$

これは、組み合わせの対称性を使います。$_nC_k=_nC_{n-k}$というやつです。これを使うと、

$$
\sum_{i=0}^k{
\begin{pmatrix}a\\i\end{pmatrix}
\begin{pmatrix}b\\k-i\end{pmatrix}
}
$$

となって、公式を使うことができるようになります。