EasyOCRで文字認識｜Pythonで写真やレシートから簡単にテキストを抽出する方法
Aru
Aru's テクログ（Aruaru0）
【Python】配列（リスト）で二分探索木（BST）を実装する｜ポインタを使わない方法
Aru
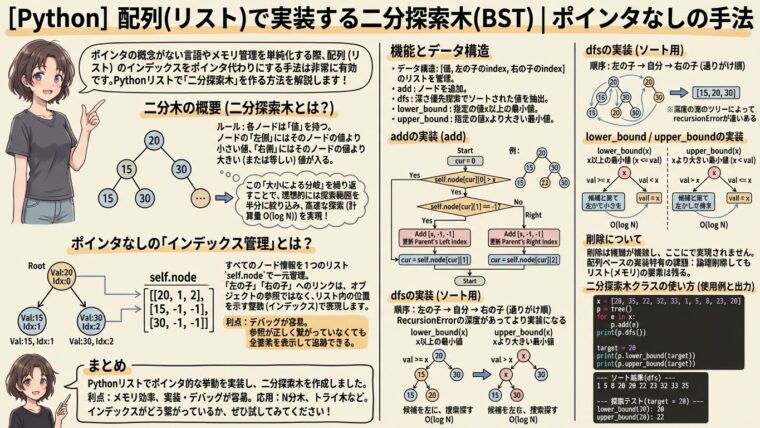
アルゴリズム本を読むと、木構造を作る場合は構造体とポインタを利用してノード同士を繋げることが一般的です（C言語など）。 しかし、ポインタの概念がない言語や、メモリ管理を単純化したい場合は、配列（リスト）のインデックスをポインタの代わりとして使う手法が非常に有効です。この記事では、Pythonのリストを使って「二分探索木（Binary Search Tree）」を作成する方法を解説します。
Contents
二分木の概要（二分探索木とは）
今回作成する二分木は、以下のルールを持つ典型的な二分探索木です。この二分探索木は以下のような構造になります。
- 各ノードは「値」を持つ
- あるノードの「左側」には、そのノードの値より小さい値が入る。
- あるノードの「右側」には、そのノードの値より大きい（または等しい）値が入る
この「大小関係による分岐」が繰り返されることで、理想的な状態では1回進むごとに探索範囲が半分になり、高速な検索（計算量 $O(\log N)$）を実現できるデータ構造になります。
ただし、値の挿入順が偏ると木が一直線になり、最悪計算量は O(N) になります。本記事では構造理解を目的とし、自己平衡木は扱いません。
平衡二分木などは、左右が不均等になった場合にバランシングする機能などを持ち複雑です。
リンク
ポインタを使わない「インデックス管理」とは？
一般的に、木を作る場合には、各ノードに対応するオブジェクトを生成し、これを繋げていく手法を取ります。つまり、参照（ポインタ）による連結により木構造を構築するわけです。
しかし、今回紹介する方法では、すべてのノード情報を 1つのリスト self.node に順番に詰め込んで一元管理 します。「左の子」や「右の子」へのリンクは、オブジェクトへの参照ではなく、「そのノードがリストの何番目に格納されているか」という整数（インデックス） を使って表現します。 これは、メモリのアドレス（住所）で相手を探すのではなく、リスト内での通し番号でノードを示す形になります。
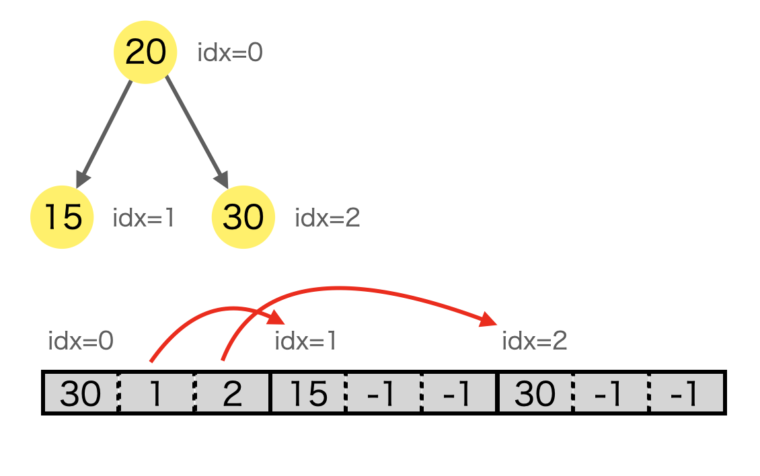
木構造の視覚的なイメージと、実際にプログラム内部で保持されるデータ構造の対応関係は以下のようになります。
- 左側（木のイメージ）
ルートノード（値:20, インデックス:0）を頂点とし、その左下に子ノード（値:15, インデックス:1）、右下に子ノード（値:30, インデックス:2）が枝分かれして繋がっている図を想像してください。 - 右側（リストの中身）
プログラム内では、リストself.nodeは以下のような構造になります。[[20, 1, 2], [15, -1, -1], [30, -1, -1]] - 説明と対応付け
- インデックス0 (
[20, 1, 2])
値は20です。左の子はインデックス1に、右の子はインデックス2にあることを示しています。 - インデックス1 (
[15, -1, -1])
値は15です。左右のインデックスが-1となっています。これは「子が存在しない（行き止まり）」ことを意味し、このノードが「葉（リーフ）」であることを表します。 - インデックス2 (
[30, -1, -1])
値は30です。同様に子を持たない葉ノードです。
- インデックス0 (
このように、リストの各要素が [値, 左の子へのID, 右の子へのID] という固定フォーマットを持つことで、ポインタを使わずに木構造を完全に表現できます。
配列を使った木構造のメリットは、デバッグしやすい点です。参照が正しく繋がっていなくても、全体の要素を表示することができるので、接続の間違いを追いやすいです。
用意する関数とデータ構造
今回は以下の機能を持つ tree クラスを作成します。
- データ構造:
[値, 左の子のインデックス, 右の子のインデックス]というリストを管理。 add: ノードを追加する。dfs: 深さ優先探索（DFS）で木を巡回し、ソートされた順序で値を取り出す。lower_bound: 指定した値 $x$ 以上の最小の値を探す。upper_bound: 指定した値 $x$ より大きい最小の値を探す。
データ構造（__init__）
コンストラクタでは、木の実体となるリストを初期化するだけです。
class tree :
def __init__(self) :
self.node = []各ノードは [val, left, right] の3要素を持つリストとして self.node に追加されていきます。ここで left や right が -1 の場合は、「子が存在しない（None）」ことを表します。
追加（add）の実装
新しい値を追加するメソッドです。ルート（インデックス0）からスタートして、以下のロジックで場所を探します。
- 挿入したい値
xが現在のノードの値より小さい場合 → 左へ進む。 - 挿入したい値
xが現在のノードの値より大きい場合 → 右へ進む。 - もし進む先のインデックスが
-1（行き止まり）なら、そこに新しいノードを作成する。
def add(self, x) :
# 木が空の場合、最初のノード（ルート）として追加
if len(self.node) == 0 :
self.node.append([x, -1, -1]) # (val, left, right)
return
cur = 0 # ルートから探索開始
while cur != -1 :
if self.node[cur][0] > x : # 現在の値 > x なら左へ
if self.node[cur][1] == -1 : # 左が空ならここに追加
self.node.append([x, -1, -1])
# 親ノードのleftを、今追加したノードのインデックス（末尾）に更新
self.node[cur][1] = len(self.node) - 1
return
cur = self.node[cur][1] # 左の子へ移動
else : # 現在の値 <= x なら右へ
if self.node[cur][2] == -1 : # 右が空ならここに追加
self.node.append([x, -1, -1])
# 親ノードのrightを、今追加したノードのインデックス（末尾）に更新
self.node[cur][2] = len(self.node) - 1
return
cur = self.node[cur][2] # 右の子へ移動
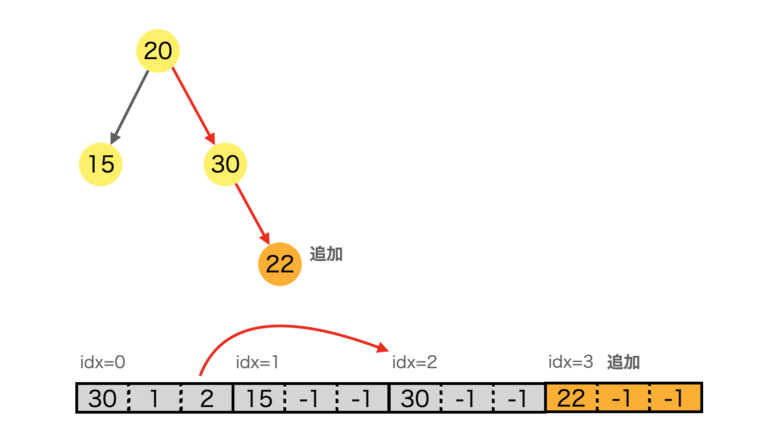
- ステップ1： ルート（値20）と比較。追加したい値（例えば22）が大きいので「右（インデックス2）」へ進む指示が出る。
- ステップ2： インデックス2のノード（値30）と比較。22は小さいので「左」へ行こうとする。
- ステップ3： 左が
-1なので、リストの末尾に[22, -1, -1]を追加し、親（値30）の左ポインタを新しいインデックスに書き換える様子。
dfsの実装（ソートとしての利用）
二分探索木は、「左の子 → 自分 → 右の子」の順（通りがけ順／In-order）で巡回すると、値が小さい順（昇順）に取り出せるという性質があります。このような探索は深さ優先探索（DFS）で行うことが可能です。
ここでは、木の中身をソートされたリストとして返す dfs() を実装します。
def dfs(self, cur=0) :
if cur == -1 : # 行き止まりなら空リストを返す
return []
# 左の部分木を探索
ret = self.dfs(self.node[cur][1])
# 自分自身の値を追加
ret.append(self.node[cur][0])
# 右の部分木を探索して結合
ret += self.dfs(self.node[cur][2])
return ret
ノード数が非常に多い場合や、木が片側に偏った場合は
再帰が深くなり RecursionError が出る可能性があります。
対応方法は、以下のブログ記事を参照してください。
Python初心者がAtCoderでハマりがちなポイント解説（キュー処理・再帰処理など）
lower_bound, upper_boundの実装
二分探索木の強みである「特定の値以上の値」などを検索する機能も実装してみます。 、条件を満たす値の検索は、計算量 $O(\log N)$ でできます。
lower_bound ($x \le val$)
「$x$ 以上の値の中で最小のもの」を探します。
- 現在の値が $x$ 以上なら、条件を満たすので候補として保持 (
ret = val) しつつ、もっと小さい値がないか左側を探しに行きます。 - 現在の値が $x$ より小さければ、条件を満たさないので右側を探しに行きます。
# x以上の最小の値を返す (x <= val)
def lower_bound(self, x):
if not self.node:
return None
cur = 0
ret = None
while cur != -1:
val = self.node[cur][0]
if val >= x: # 条件を満たす
ret = val # 暫定解として記録
cur = self.node[cur][1] # より小さい解があるか左へ
else: # xより小さい（条件を満たさない）
cur = self.node[cur][2] # 大きな値がある右へ
return retupper_bound ($x < val$)
「$x$ より大きい値の中で最小のもの」を探します。ロジックは lower_bound とほぼ同じですが、比較条件が val > x になります。
# xより大きい最小の値を返す (x < val)
def upper_bound(self, x):
if not self.node:
return None
cur = 0
ret = None
while cur != -1:
val = self.node[cur][0]
if val > x: # 条件を満たす
ret = val
cur = self.node[cur][1]
else: # x以下（条件を満たさない）
cur = self.node[cur][2]
return ret
削除（delete）について
今回は、delete（ノードの削除）機能は実装しません。二分探索木における削除処理は、追加や探索に比べて条件分岐が多く、実装が複雑になるためです。
deleteの実装方法としては、例えば以下のようなケース分けが必要になります。
- 削除するノードが「葉（子なし）」の場合: 親ノードからの参照（インデックス）を
-1に変更するだけで済みます。 - 削除するノードが「子を1つ持つ」場合: 削除するノードの親が、削除するノードの子を直接指すようにリンクを繋ぎ変えます。
- 削除するノードが「子を2つ持つ」場合: これが最も複雑です。削除するノードの「右部分木の中で最小の値」を持つノード（または左部分木の最大）を探し出し、その値を削除対象の場所にコピーします。その後、値の移動元となったノードを削除します（再帰的に1か2のケースに帰着します）。
面倒なのは、削除するノードが子を持つ場合の２つの場合の実装です。上記のアルゴリズムを実装すれば良いので、興味のある方は実装に挑戦してみてください。
なお、「配列ベース」の実装特有の課題もあります。 ノードを論理的に削除しても、リスト上の要素（メモリ）はそのまま残ります。実務レベルでメモリの効率を考えて実装する場合は、削除済みで再利用可能なインデックスを管理する仕組みを導入する必要があります。
二分探索木クラスの使い方（実行例）
実際にこのクラスを使って、データの追加と探索を行ってみます。
# データの準備
x = [20, 35, 22, 32, 33, 1, 5, 8, 23, 20]
print(f"入力データ: {x}")
# 木の構築
p = tree()
for e in x :
p.add(e)
# 内部構造（リスト）の確認
# [値, 左ID, 右ID] のリストが並んでいるのがわかります
print("\n--- 内部構造 (self.node) ---")
print(p.node)
# DFSによるソート結果の出力
r = p.dfs()
print("\n--- ソート結果 (dfs) ---")
print(*r)
# 50を追加して再度確認
p.add(50)
print("\n--- 50を追加後のソート結果 ---")
print(*p.dfs())
# 探索のテスト
target = 20
print(f"\n--- 探索テスト (target = {target}) ---")
print(f"lower_bound({target}): {p.lower_bound(target)}") # 20 (20以上で最小)
print(f"upper_bound({target}): {p.upper_bound(target)}") # 22 (20より大きく最小)
出力結果の解説
実行結果
入力データ: [20, 35, 22, 32, 33, 1, 5, 8, 23, 20]
--- 内部構造 (self.node) ---
[[20, 5, 1], [35, 2, -1], [22, 9, 3], [32, 8, 4], [33, -1, -1], [1, -1, 6], [5, -1, 7], [8, -1, -1], [23, -1, -1], [20, -1, -1]]
--- ソート結果 (dfs) ---
1 5 8 20 20 22 23 32 33 35
--- 50を追加後のソート結果 ---
1 5 8 20 20 22 23 32 33 35 50
--- 探索テスト (target = 20) ---
lower_bound(20): 20
upper_bound(20): 22上記のコードを実行すると、dfs() の結果が昇順にソートされていることが確認できます。
また、探索のテスト結果にも注目してください。
lower_bound(20)は20そのものを返します。「20以上」という条件には20自身が含まれるためです。upper_bound(20)は22を返します。「20より大きい」という条件のため、20の次に大きい値である22が選ばれます。
このように、リストだけで構成した木構造でも、ポインタを使った場合と同じように正しく探索ができていることがわかります。
プログラム全体
今回のプログラム全体です
class tree :
def __init__(self) :
self.node = []
def add(self, x) :
# 木が空の場合、最初のノード（ルート）として追加
if len(self.node) == 0 :
self.node.append([x, -1, -1]) # (val, left, right)
return
cur = 0 # ルートから探索開始
while cur != -1 :
if self.node[cur][0] > x : # 現在の値 > x なら左へ
if self.node[cur][1] == -1 : # 左が空ならここに追加
self.node.append([x, -1, -1])
# 親ノードのleftを、今追加したノードのインデックス（末尾）に更新
self.node[cur][1] = len(self.node) - 1
return
cur = self.node[cur][1] # 左の子へ移動
else : # 現在の値 <= x なら右へ
if self.node[cur][2] == -1 : # 右が空ならここに追加
self.node.append([x, -1, -1])
# 親ノードのrightを、今追加したノードのインデックス（末尾）に更新
self.node[cur][2] = len(self.node) - 1
return
cur = self.node[cur][2] # 右の子へ移動
def dfs(self, cur=0) :
if cur == -1 : # 行き止まりなら空リストを返す
return []
# 左の部分木を探索
ret = self.dfs(self.node[cur][1])
# 自分自身の値を追加
ret.append(self.node[cur][0])
# 右の部分木を探索して結合
ret += self.dfs(self.node[cur][2])
return ret
# x以上の最小の値を返す (x <= val)
def lower_bound(self, x):
if not self.node:
return None
cur = 0
ret = None
while cur != -1:
val = self.node[cur][0]
if val >= x: # 条件を満たす
ret = val # 暫定解として記録
cur = self.node[cur][1] # より小さい解があるか左へ
else: # xより小さい（条件を満たさない）
cur = self.node[cur][2] # 大きな値がある右へ
return ret
# xより大きい最小の値を返す (x < val)
def upper_bound(self, x):
if not self.node:
return None
cur = 0
ret = None
while cur != -1:
val = self.node[cur][0]
if val > x: # 条件を満たす
ret = val
cur = self.node[cur][1]
else: # x以下（条件を満たさない）
cur = self.node[cur][2]
return ret
# データの準備
x = [20, 35, 22, 32, 33, 1, 5, 8, 23, 20]
print(f"入力データ: {x}")
# 木の構築
p = tree()
for e in x :
p.add(e)
# 内部構造（リスト）の確認
# [値, 左ID, 右ID] のリストが並んでいるのがわかります
print("\n--- 内部構造 (self.node) ---")
print(p.node)
# DFSによるソート結果の出力
r = p.dfs()
print("\n--- ソート結果 (dfs) ---")
print(*r)
# 50を追加して再度確認
p.add(50)
print("\n--- 50を追加後のソート結果 ---")
print(*p.dfs())
# 探索のテスト
target = 20
print(f"\n--- 探索テスト (target = {target}) ---")
print(f"lower_bound({target}): {p.lower_bound(target)}") # 20 (20以上で最小)
print(f"upper_bound({target}): {p.upper_bound(target)}") # 22 (20より大きく最小)
まとめ
今回はPythonのリストを使ってポインタのような振る舞いを実装し、二分探索木を作成しました。
- メリット
クラスのインスタンスを大量に生成するよりもメモリ効率が良い場合がある。実装が簡単でデバッグがやりやすい。 - 応用
実装方法を覚えていればN分木なども簡単に作ることができます。応用としてトライ木なども実装可能です。
ぜひ手元で動かして、インデックスがどのように繋がっていくかを確認してみてください。
ABOUT ME
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
