次元圧縮｜PCA, t-SNE, UMAPで高次元データを可視化する【初級 深層学習講座】
Aru
Aru's テクログ（Aruaru0）
XORで学ぶ多層ニューラルネットワークの学習と推論【初級 深層学習講座】
Aru
このブログ記事では、ニューラルネットワークの基本的な仕組みを解説し、特にその学習に不可欠な活性化関数の重要性を掘り下げます。ANDやORとは異なり、1本の直線では分類できないXORの問題を例に、なぜ多層ネットワークが必要なのかを丁寧に解説します。さらに、PyTorchを使った具体的な実装を通して、非線形な問題であるXORをディープラーニングでどのように解くのかを学びます。線形変換だけでは表現力が増えないことや、活性化関数が非線形性を導入する役割を、コードとグラフを用いて視覚的に理解できます。
Contents
ニューラルネット
ニューラルネットワークの基本計算
ニューラルネットワークのニューロンは、基本的に次の計算を行います。ここで、$w$は重み係数で、$b$はバイアス（オフセット）です。
$$ y = wx+b$$
入力が２変数$x_1, x_2$の場合は次の式になります。
$$ y = w_1 x_1 + w_2 x_2 + b $$
これを入力がN個に一般化すると、次式になります。
$$
y = \sum_{i = 1}^N{w_i x_i} + b
$$
このように、ニューラルネットワークでは入力数に応じてパラメータを持つ計算を行います。
線形変換を多層化しても意味がない理由
しかし、線形変換だけを何層重ねても意味がありません。
例えば、変換$f(x) = wx + b$を考えます。
中間層の出力は次のようになります。
$$ h = f(x) = w_1x+b_1$$
これを次の層に入力すると、
$$
\begin{eqnarray}
y &=& f(h) \\
&=&w_2(w_1x + b_1) + b_2\\
&=& w_1w_2x + w_2b_1 + b_2
\end{eqnarray}
$$
ここで、$w’ = w_1w_2$, $b’ = w_2b_1 + b_2$とおくと、
$$y = w’x + b’$$
となり、結局は1層の線形変換と同じ形に帰着してしまいます。
つまり、線形変換を重ねても表現力は増えません。
活性化関数
この問題を解決するためにニューラルネットワークでは、「活性化関数」という非線形関数を途中に挟みます。
活性化関数としては、シグモイドやReLUなどがあります。
例えば、シグモイドは以下の式になります。
$$
\sigma(x) = \frac{1}{1+e^{-x}}
$$
この関数をグラフにすると、以下のように入力を0~1に写像する曲線になります。。
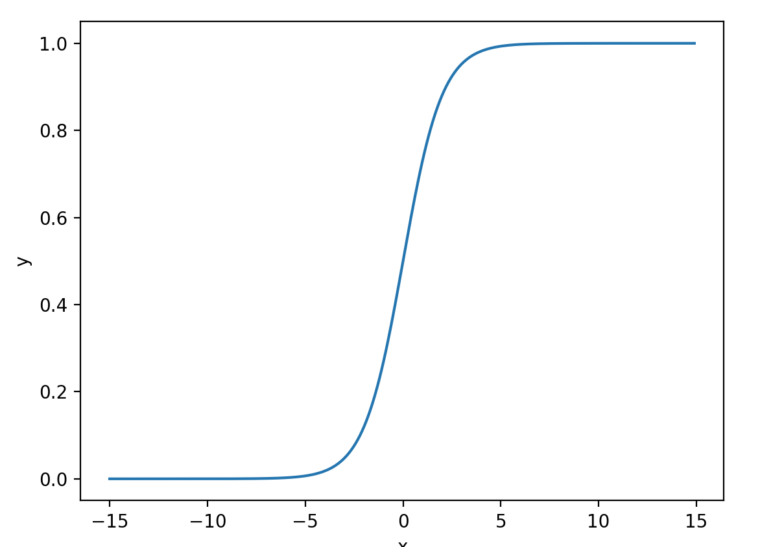
このように非線形を導入することで、複数層を組み合わせる意味が生まれます。
ちなみに、$w_i=1, b_i=0$として２層のネットワークを計算すると以下のようになります。
$$
\begin{eqnarray}
f(h)& =& (w_1x+b_1) \\
&=&x\\
\end{eqnarray}
$$
$$
\begin{eqnarray}
y &=& f(\sigma(f(h)) \\
y &=& w_2\sigma(x) x + b_2\\
y &=& \sigma(x) x\\
y &=& \frac{x}{1+e^{-x}}
\end{eqnarray}
$$
この関数をグラフ化し、$y$と$x$の関係をみると次図のように曲線になることがわかります。
このように、活性化関数を層の間に追加することで、曲線による分割を行うことができるようになります。これにより、表現力（分割能力）を増やすことが可能となります。
以下では、AND,OR,XORの出力を返すニューラルネットワークを例、線形関数での限界について深掘りしてみます。
論理式（AND,OR,XOR）
次に、入力X1, X2に対して AND, OR, XOR の出力を返すニューラルネットワークを考えてみます。
ANDの例
図はANDの例です。
左のグラフはX1とX2が(0,0), (0,1), (1,0), (1,1)の場合の出力値を二次元平面に配置したものです。右の表はANDの入力(X1, X2)と出力Yの関係表です。
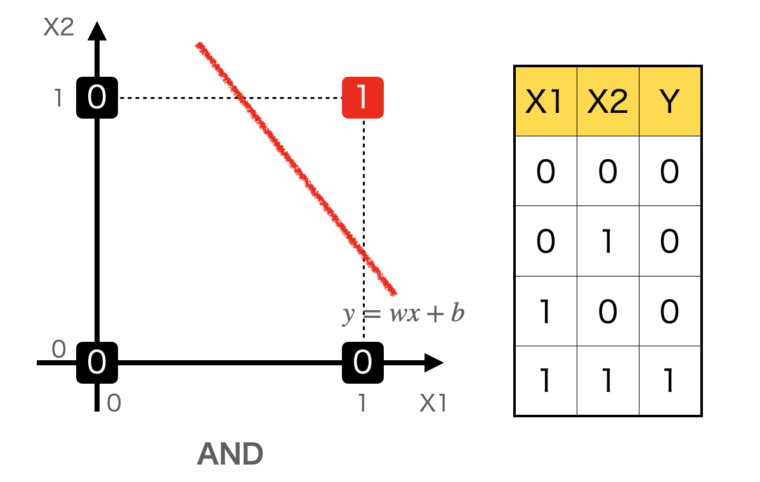
図を見ると、直線$y=w_1x_1+w_2x_2b$で、0と1を区分することができることがわかります。
正確には、$y$、$x1$, $x2$の３次元で、直線ではなく平面で区分が正確かもしれませんが、ここでは分かりやすくするために２次元で表現しています。
より厳密な説明
ニューラルネットの出力は$y = w_1x_1 + w_2x_2 + b$という式で表すことができます。$y$が0より大きければ1、小さければ0と判定する場合、0/1の境界は以下の式で表すことができます。
$$y = w_1x_1 + w_2x_2 + b = 0$$
これを$x_2 = $の形に変形すると、以下になります。
$$
x_2 = \frac{w_1}{w_2} x_1 + \frac{w_2}{b} = w’x_1 + b’
$$
ここで、以下のように$w’, b’$を定義すると、
$$
w’ = \frac{w_1}{w_2}, b’ = \frac{b}{w_2}
$$
数式は、以下のように直線グラフになります。
$$
x_2 = w’x_1 + b’
$$
この直線が出力の0と1の境界になるので、この直線で「０のグループ」と「１のグループ」を分割できれば良いことになります。
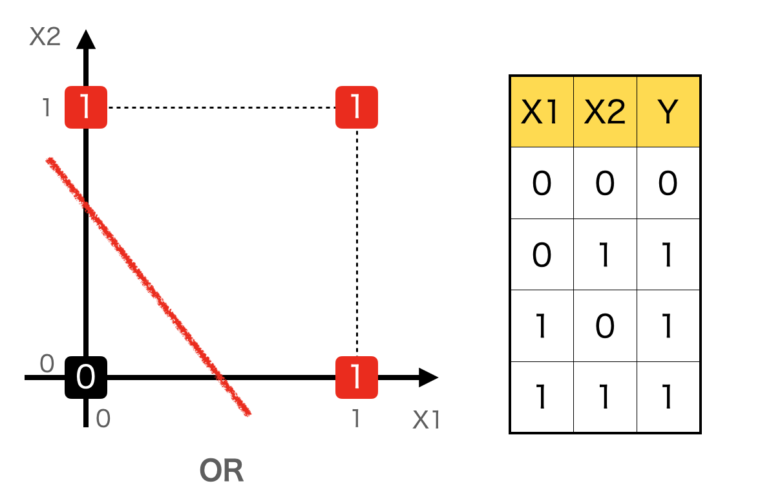
ORの例
ORも同様にみてみます。こちらも、直線１本で0と1を区分することができます。
XORの例
では、XORの場合をみてみましょう。
XORは入力が(0,1)または(1,0)の時に、1を出力し、それ以外は0を返します。
下図を見てわかるように、どのように直線を引いても、0と1を区分することはできません。区分したい場合は、図の赤線のような曲線（非線形な方程式）で分ける必要があります。
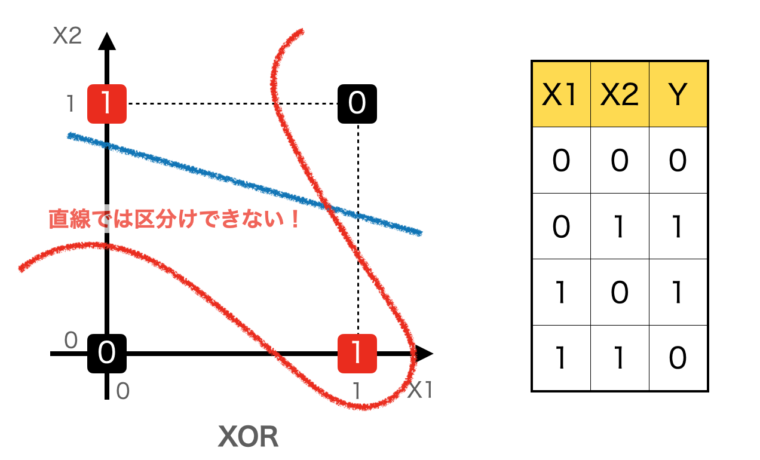
このように、XORを学習させるには非線形な変換が不可欠です。
実際、1層の線形変換だけではXORを学習できません。
必要なのは、
- 線形変換
- 活性化関数による非線形変換
- さらに線形変換
という多層のネットワーク構造です。
なお、「線形変換＋活性化関数」 を1つの層と定義するのが一般的です。
XORを学習させてみる
これまで見てきたように、ANDやORは直線で分離できるため1層のニューラルネットワークでも表現できます。しかしXORは直線で分離できず、1層のネットワークでは学習できません。そこで、実際にPyTorchを使って多層（2層）のニューラルネットワークを構築し、XORの学習を試してみます。
実装
ライブラリの読み込み
まずは必要なライブラリをインポートします。PyTorchを使ってニューラルネットワークを定義・学習し、matplotlibを使ってグラフ描画を行います。
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt乱数を固定化
ニューラルネットワークの学習は乱数に依存します。何度実験しても同じ結果になるように（同じ結果が再現できるように）、乱数をシードを使って固定しておきます。
seed = 42
torch.manual_seed(seed)
np.random.seed(seed)これでプログラムを毎回実行しても同じ結果が得られるようになります。
入力データと正解ラベルの作成
XORの入力と出力を定義します。入力は2ビットの組み合わせ、出力はそのXOR結果です。このシンプルな4つのデータが学習対象となります。
それぞれPyTorchのテンソル型で定義します。
#データ
X=torch.tensor([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0],[1.0, 1.0]] )
#ラベル（正解） XOR
y=torch.tensor([[0.0],[1.0],[1.0],[0.0]])ANDの場合は以下のようなデータを用意します、入力Xは共通です。
#データ
X=torch.tensor([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0],[1.0, 1.0]] )
#ラベル（正解） AND
y=torch.tensor([[0.0],[0.0],[0.0],[1.0]])モデル定義
次に、ニューラルネットワークを定義します。隠れ層を1層持つシンプルな全結合ネットワークを作成します。
model = nn.Sequential(
nn.Linear(2,2),
nn.Sigmoid(),
nn.Linear(2,1),
nn.Sigmoid()
)ここで重要なのは、先ほど説明したように、活性化関数 Sigmoid を入れることで非線形性をモデルに取り入れている点です。これがあることでXORのような非線形問題を解けるようになります。
一層のニューラルネットワークも試してみると面白いでしょう。
モデルは以下のようになります。
model = nn.Sequential(
nn.Linear(2,1),
nn.Sigmoid()
)出力にSigmoidがあるのは、Linearの出力はマイナスからプラスまでどんな値でも出てしまうためです。 Sigmoidを挿入することで「0〜1の範囲」に変換することができ、正解ラベルの 0 や 1 と比較できるようになります。
学習ループ
損失関数（誤差の指標）と最適化アルゴリズムを設定し、学習を繰り返します。ここでは20,00回繰り返して学習を行います。loss（損失）が小さくなっていく様子を確認できます。
model.train()
loss_fn = nn.BCELoss()
optimizer = torch.optim.SGD(params = model.parameters() , lr = 0.1)
losses = []
for epoch in range(20000):
optimizer.zero_grad()
t_p = model(X)
# 損失計算と逆電波
loss = loss_fn(t_p,y)
loss.backward()
# SGD法による更新
optimizer.step()
#100エポック毎に損失の値を表示
if epoch % 100 == 0:
print("epoch: %d loss: %f" % (epoch ,float(loss)))
losses.append(loss.item())loss_fn は 損失関数（Loss Function） で、モデルの出力と正解ラベルとの誤差を数値として評価するためのものです。ここではバイナリ分類用の BCELoss を使っています。
optimizer は 最適化関数 で、モデルのパラメータ（重みやバイアス）を更新して損失を小さくする役割を持ちます。今回は確率的勾配降下法（SGD）を使っています。
for ブロックの中では、以下の手順を繰り返しています：
- モデルに入力データを渡して予測を計算（順伝播）
- 損失関数で予測と正解の誤差を計算
backward()で逆伝播を行い、誤差を各パラメータに伝えるoptimizer.step()でパラメータを更新
この流れを繰り返すことで、モデルは少しずつ XOR のパターンを正しく予測できるようになります。
学習結果
最後に、学習の過程で損失がどのように減っていったのかを可視化します。
plt.plot(losses)
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Training Loss for XOR Problem")
plt.show()実行すると、損失が徐々に下がっていくグラフが描かれ、モデルが学習していることがわかります。また、実際に学習後のモデルに入力を与えてみると、XORの結果を正しく予測できるようになっているはずです。
グラフを見ると10,000回目あたりから急激に損失が減っていることがわかります。
中間層を２つにしたので学習が遅いです。中間層を増やせば、学習は早くなります。
model = nn.Sequential(
nn.Linear(2,16),
nn.Sigmoid(),
nn.Linear(16,1),
nn.Sigmoid()
)興味がある方は試してみてください。
結果をグラフ化
最後に、学習したモデルがどのように入力を分類しているのかを可視化してみます。
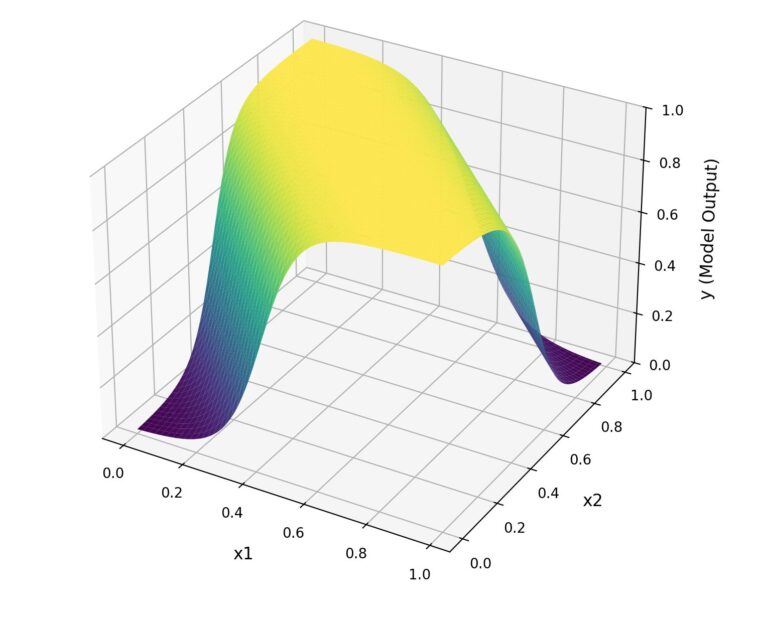
具体的には、入力 x1,x2を0から1の範囲で少しずつ変化させ、モデルが出力する値（推論結果）を3Dグラフにプロットします。
- 横軸：入力の1つ目（
x1） - 縦軸：入力の2つ目（
x2） - 高さ（Z軸）：モデルが出力した確率（0〜1の範囲）
こうすることで、ニューラルネットが「0になるべき場所」「1になるべき場所」をどのように区別しているのかを、直感的に理解できます。
# --------------------
# 2. 学習後のモデルパラメータを取得し、可視化
# --------------------
# モデルを評価モードに設定
model.eval()
def model_output(x1, x2):
x_input = np.stack([x1, x2], axis=-1)
x = torch.tensor(x_input, dtype=torch.float32).reshape(-1, 2)
y = model(x)
return y.detach().reshape(len(x1), len(x1)).numpy()
x1_range = np.arange(0, 1, 0.01)
x2_range = np.arange(0, 1, 0.01)
X_grid, Y_grid = np.meshgrid(x1_range, x2_range)
Z = model_output(X_grid, Y_grid)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X_grid, Y_grid, Z, cmap='viridis')
ax.set_xlabel('x1', fontsize=12, labelpad=10)
ax.set_ylabel('x2', fontsize=12, labelpad=10)
ax.set_zlabel('y (Model Output)', fontsize=12, labelpad=10)
ax.set_title('XOR Problem output', fontsize=14)
ax.set_zlim(0, 1)
plt.show()XORの場合、(0,0) や (1,1) のときは出力が 0 に近く、(0,1) や (1,0) のときは出力が 1 に近くなるはずです。
3Dグラフを確認すると、実際にそのような形になっており、モデルがXORを正しく学習できたことが視覚的にわかります。
また、直線的ではなく、複雑な判定を行なっていることもグラフで確認することができます。
プログラム全体
以下、プログラムコード全体です。
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
seed = 42
torch.manual_seed(seed)
np.random.seed(seed)
#データ
X=torch.tensor([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0],[1.0, 1.0]] )
#ラベル（正解） XOR
y=torch.tensor([[0.0],[1.0],[1.0],[0.0]])
model = nn.Sequential(
nn.Linear(2,2),
nn.Sigmoid(),
nn.Linear(2,1),
nn.Sigmoid()
)
# #データ
# X=torch.tensor([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0],[1.0, 1.0]] )
# #ラベル（正解） AND
# y=torch.tensor([[0.0],[0.0],[0.0],[1.0]])
# model = nn.Sequential(
# nn.Linear(2,1),
# nn.Sigmoid()
# )
model.train()
loss_fn = nn.BCELoss()
optimizer = torch.optim.SGD(params = model.parameters() , lr = 0.1)
losses = []
for epoch in range(20000):
optimizer.zero_grad()
t_p = model(X)
# 損失計算と逆電波
loss = loss_fn(t_p,y)
loss.backward()
# SGD法による更新
optimizer.step()
#100エポック毎に損失の値を表示
if epoch % 100 == 0:
print("epoch: %d loss: %f" % (epoch ,float(loss)))
losses.append(loss.item())
plt.plot(losses)
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Training Loss for XOR Problem")
plt.show()
# --------------------
# 2. 学習後のモデルパラメータを取得し、可視化
# --------------------
# モデルを評価モードに設定
model.eval()
def model_output(x1, x2):
x_input = np.stack([x1, x2], axis=-1)
x = torch.tensor(x_input, dtype=torch.float32).reshape(-1, 2)
y = model(x)
return y.detach().reshape(len(x1), len(x1)).numpy()
# Create a grid for x1 and x2 in the range [0, 1]
x1_range = np.arange(0, 1, 0.01)
x2_range = np.arange(0, 1, 0.01)
X_grid, Y_grid = np.meshgrid(x1_range, x2_range)
# Calculate the model's output (y) for each point in the grid
Z = model_output(X_grid, Y_grid)
# Create the 3D plot
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# Plot the surface
ax.plot_surface(X_grid, Y_grid, Z, cmap='viridis')
# Set labels and title
ax.set_xlabel('x1', fontsize=12, labelpad=10)
ax.set_ylabel('x2', fontsize=12, labelpad=10)
ax.set_zlabel('y (Model Output)', fontsize=12, labelpad=10)
ax.set_title('XOR Problem output', fontsize=14)
ax.set_zlim(0, 1)
plt.show()
# You can save the figure to a file instead of displaying it
# plt.savefig('xor_model_3d_plot.png')まとめ
この記事では、ニューラルネットワークの基本構造を説明し、非線形関数（活性化関数）がニューラルネットワークの学習には重要なことを説明しました。
また、XOR問題を題材に、ニューラルネットワークの基本的な流れを解説しました。
XORは小さな例ですが、「ニューラルネットワークがなぜ必要か」「活性化関数がなぜ大事か」を直感的に理解できる題材です。小さなプログラムですし、CPUでも十分高速に試すことができるので、色々書き換えてチャレンジしてみるのも面白いでしょう。
ABOUT ME
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
