検定・機械学習の前処理でよく使う標準化について

tadanori

標準化とは

標準化とは平均$\mu$、分散$\sigma ^2$の確率分布に従う確率変数Xを平均0、分散1の確率分布の確率変数Zに変換する操作です。

正確な図ではないですがこんなイメージになります。横軸は項目の番号で$x_i$の$i$に対応しています。縦軸は$x_i$の値です。

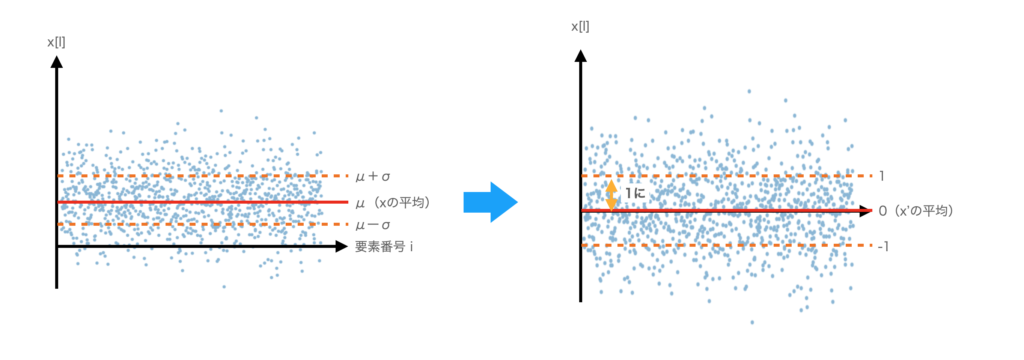
例えば、点のように分布している場合、平均$\mu = \bar{x}$を赤い線、偏差$\sigma$をオレンジの線で表すと図のようになります。

まず、平均を0にする操作を考えます。平均を0にするには、$\mu$を引けばいいので、以下のようにすれば0になります。

$$
X – \mu
$$

次に分散を１（偏差も１）にします。これは幅を変化させる操作なので、割り算となります。

$$
Z = \frac{X – \mu}{\sigma}
$$

以上が標準化の操作になります。

言葉だけ聞くとなんだか難しそうですが、意外と簡単です。

応用例

互いに独立な確率変数$X_1, X_2, X_3, …, X_n$が平均$\mu$、分散$\sigma^2$に従うときに$\bar{X}$を以下のよう定義します。

$$
\bar{X} = \frac{X_1 + X_2 + X_3 + … + X_n}{n}
$$

この$\bar{X}$の平均と分散は以下のようになります。

$$ \begin{eqnarray} E[\bar{X}] &=& E \left[ \frac{X_1 + X_2 + X_3 + … + X_n}{n}\right]\\ &=& \frac{1}{n}E[X_1 + X_2 + X_3 + … + X_n]\\ &=& \frac{1}{n}\left\{ E[X_1] + E[X_2] + E[X_3] + … + E[X_n]\right\}\\ &=& \frac{1}{n}\left\{ \mu + \mu + \mu + … + \mu\right\}\\ &=& \frac{1}{n}\cdot n \mu\\ &=& \mu \end{eqnarray} $$

$$ \begin{eqnarray} V[\bar{X}] &=& V \left[ \frac{X_1 + X_2 + X_3 + … + X_n}{n}\right]\\ &=& \frac{1}{n^2}V[X_1 + X_2 + X_3 + … + X_n]\\ &=& \frac{1}{n^2}\left\{ V[X_1] + V[X_2] + V[X_3] + … + V[X_n]\right\}\\ &=& \frac{1}{n^2}\left\{ \sigma^2 + \sigma^2 + \sigma^2 + … + \sigma^2\right\}\\ &=& \frac{1}{n^2}\cdot n ^2\sigma^2\\ &=& \frac{\sigma^2}{n} \end{eqnarray} $$

ですから、$\bar{X}$の標準化は、以下のようになります。

$$
Z = \frac{\bar{X} – \mu}{\sqrt{\frac{\sigma^2}{n}}}
$$

このZの式ですが、推定・検定でよく使われているものになります。標準化はいろいろなケースで利用されますので覚えておきましょう。