巡回セールスマン問題をビットDPで解く｜PythonとGoによる実装例

巡回セールスマン問題をビットDP（動的計画法）を使って解く方法を解説します。この記事では、PythonとGo言語で巡回セールスマン問題を解くコードを紹介します。

巡回セールスマン問題とは

巡回セールスマン問題

巡回セールスマン問題とは、「N個の都市がある場合に、すべての都市をめぐって出発点に帰ってくるまでのコストを最小化する問題」です。具体的にいうと、0→….→0という経路を求める問題です。

この問題はNP問題（NP困難）と知られており、N-1都市の並べ替えは(N-1)!ありますので、計算量はO(N!)になります。

たとえば10都市の場合、(10-1)! = 9! = 362,880通りのパターンがあります。これくらいまでは、全パターン計算できなくはありませんが、14都市になると13!=6,227,020,800となり、4都市増えただけで約1.7万倍のパターンに膨れ上がります。このように、都市数に対して組み合わせが爆発するため、コンピューターで実用的な時間で解くのが難しい問題と言われています。

効率的な解法

計算量の多い巡回セールスマン問題ですが、都市数が少なければ、高速に解く方法があります。この方法を使えば16都市くらいまでは、すぐに答えを出すことが可能です。

この記事では、巡回セールスマンをbitDP（動的計画法）を使って高速に解く方法を解説します。

巡回セールスマンをビットDPを使って解く方法

解法の原理

ここで、セールスマンが0→….→mというように、都市mにいるとします。これまで通過した都市の集合をSとすると、集合Sにどの都市が入っているかだけわかれば、まだ訪問していない都市はわかります。また、実は、都市の集合Sを訪問して最後に都市mに到着した時の最短のコストだけ記録していればよく、道のりを知っている必要はありません。つまり、訪問した都市と訪問していない都市の区別がつけば良いことになります。

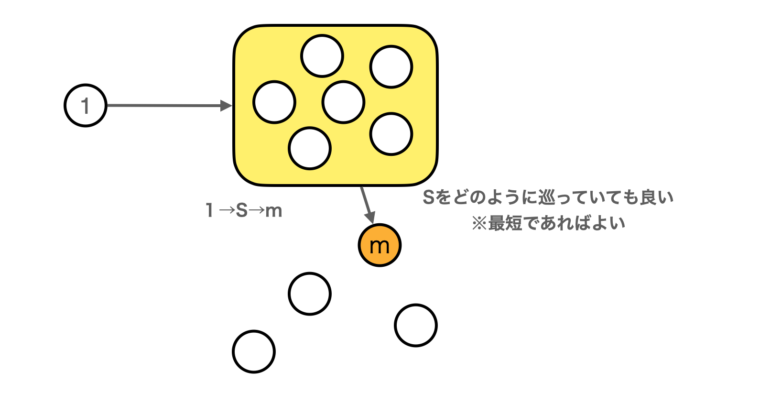
訪問した（１）と訪問していない（０）で表現する場合、都市の状態は$2^N$のパターンで表すことができ、$N!$と比較してかなり小さくなります。

bitDP（動的計画法）を使った解法では、これを利用します。

ただし、この方法には１つ問題があります。それは、「都市群Sを通過して最後に都市mに到達した場合の最小コスト」を記録しておく必要があることです。つまり、それだけメモリが必要になります。

たとえば16都市であれば、$2^16=65536$都市分のコストを記録する必要があります。この必要メモリは都市数が多くなれば多くなるほど大きくなります。

このため、都市数がある程度以上大きくなるとメモリが足りなくなるため、この手法を適用できなくなります。

ただ、都市数16程度であれば十分少ないメモリで、かつ高速に探索できます。

実際に解いてみる

AtCoderの典型アルゴリズム問題集に、ちょうどよい問題があるのでこの問題を解くプログラムを作成してみます。

問題は、

「N 個の都市があり、0,1,…,N−1 と番号付けられている。全ての異なる 2 都市の間には道が存在し、都市 i から都市 j に移動するときのコストはAi,j​ である。あなたは今都市 0 にいる。ここから都市 0 以外の都市をちょうど 1 回ずつ訪れ、都市 0 に戻ってくる経路を作りたい。そのような経路における合計コストの最小値を求めよ。」

というものです（まんま巡回セールスマン問題です）。

以下は、問題へのリンクです。

Pythonプログラム

実際にこの問題を解くプログラムは以下のようになります。

N = int(input())

a = [list(map(int, input().split())) for _ in range(N)]

n = 1 << N
inf = 10**15

# dp[i][j] : 集合ｊの都市に訪問していて、最後に訪れたのが都市i
dp = [[inf for _ in range(n)] for _ in range(N)]

# 0 -> 各都市の距離を初期化
for i in range(N):
    dp[i][1 << i] = a[0][i]

# ビットDP
for bit in range(0, n):
    for s in range(N):
        # sに訪問していなければパス
        if (bit >> s) % 2 == 0 or dp[s][bit] == inf:
            continue
        for to in range(N):
            # tに訪問していればパス
            if (bit >> to) % 2 == 1:
                continue
            dp[to][bit | (1 << to)] = min(dp[to][bit | (1 << to)], dp[s][bit] + a[s][to])

print(dp[0][n - 1])

1. Nと各都市の距離データaを読み込みます。
2. nに$2^n$を計算して代入し、infにはコストの総和としてはあり得ない大きな値（ここでは$10^15$）を設定します。
3. dp変数を初期化します。
   dp[i][S]は、集合Sの都市を訪問していて最後に訪れた都市がiの場合の最小のコストとなります。全てinfに初期化しておきます。
4. dp[i][1<<i]を都市0から都市iまでの距離で初期化します。1<<iとすることでiを訪問済みにします。都市0は訪問済みにしない部分がポイントです
5. ビットDPでを行います
   全てのパターンSについて、Sに訪問していた場合にはSに含まれていない都市への訪問した場合のコストを計算します。この時、コストが小さい場合にはdp[to]を更新します。
6. dp[0][n-1]に最小コストが格納されているのでこれを表示します

以上がアルゴリズムです。コードからわかるように、集合Sのパターン数（$2^n$）、最後に訪問した都市（N）と、次の訪問都市（N)の３重ループになり、計算量は$O(n^2 2^n)$となります。$n!$と比べるとかなり少ない演算量だということがわかります。

「都市0は訪問済みにしない」ことで、dp[0][n-1] に「全ての都市を巡回した最小コスト」が格納されます。もし dp[0][0] = 0 から探索すると、最後に訪れた都市から都市0に戻るコストを別途足す処理が必要になります。

Goプログラム

同じプログラムをGo言語で記述しています。基本的には同じですが、Go言語の場合は標準入出力を高速化するためにbufioパッケージを使っています。

あわせて読みたい

Go言語でAtCoder参加時のテンプレートと注意すべきポイント

package main

import (
	"bufio"
	"fmt"
	"math"
	"os"
	"strconv"
)

var sc = bufio.NewScanner(os.Stdin)
var wr = bufio.NewWriter(os.Stdout)

func getI() int {
	sc.Scan()
	i, e := strconv.Atoi(sc.Text())
	if e != nil {
		panic(e)
	}
	return i
}

func getInts(N int) []int {
	ret := make([]int, N)
	for i := 0; i < N; i++ {
		ret[i] = getI()
	}
	return ret
}

// min, max, asub, absなど基本関数
func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func main() {
	defer wr.Flush()
	sc.Split(bufio.ScanWords)
	sc.Buffer([]byte{}, math.MaxInt32)

	N := getI()
	a := make([][]int, N)
	for i := 0; i < N; i++ {
		a[i] = getInts(N)
	}

	n := 1 << N
	const inf = int(1e15)
	dp := make([][]int, N)
	for i := 0; i < N; i++ {
		dp[i] = make([]int, n)
		for j := 0; j < n; j++ {
			dp[i][j] = inf
		}
	}

	for i := 0; i < N; i++ {
		dp[i][1<<i] = a[0][i]
	}

	for bit := 0; bit < n; bit++ {
		for from := 0; from < N; from++ {
			if (bit>>from)%2 == 0 || dp[from][bit] == inf {
				continue
			}
			for to := 0; to < N; to++ {
				if (bit>>to)%2 == 1 {
					continue
				}
				dp[to][bit|(1<<to)] = min(dp[to][bit|(1<<to)], dp[from][bit]+a[from][to])
			}
		}
	}

	fmt.Println(dp[0][n-1])
}

まとめ

巡回セールスマンを動的計画法をつかって解く方法について解説しました。この問題は$O(N!)$として説明されますが、都市数が小さい場合は動的計画法を使って高速に解くことができることがわかるかと思います。

ある/Aru

IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)

XContact

専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中