MENU
初級ディープラーニング
記事内に商品プロモーションを含む場合があります

逆伝播をビジュアライズ！ANDゲートで学ぶ学習の仕組み【初級 深層学習講座】

Aru

ニューラルネットワークの逆伝播のイメージを掴むのは結構難しいです。この記事では、逆伝播をビジュアライズして理解する助けを試みました。学習の肝ともいうべき逆伝播の理解の助けになれば幸いです。

あわせて読みたい
PyTorchの逆伝播を関数を自作して理解する【初級 深層学習講座】
PyTorchの逆伝播を関数を自作して理解する【初級 深層学習講座】
Contents
  1. はじめに
  2. ANDの学習モデルを作成し学習させる
  3. 学習過程を可視化する
  4. 全プログラムリスト
  5. まとめ

はじめに

ニューラルネットワークの学習の根幹をなすアルゴリズム、「逆伝播（バックプロパゲーション）」。数式で理解しようとすると少し難解に感じるかもしれませんが、その挙動を視覚的に捉えることで、何が行われているのかを直感的に理解することができます。

この記事では、最もシンプルな問題の一つであるANDゲートの学習を通して、逆伝播がどのようにして最適なパラメータ（重みとバイアス）を見つけ出すのかをビジュアライズ（可視化）していきます。

ANDゲートやORゲートのような「線形分離可能」な問題は、2入力1出力の「線形層」（パーセプトロンとも呼ばれます）1つだけで解くことができます。２入力１出力の線形層は、次の式で表すことができます。

$$ y = w_1x_1 + w_2x_2 + b $$

この式は、入力$x_1$と$x_2$の2次元空間上に、一本の「境界線」を引くことを意味します。学習とは、この直線がデータを正しく分離できるように、パラメータである$w_1​,w_2​,b$を調整していくプロセスです。

あわせて読みたい
XORで学ぶ多層ニューラルネットワークの学習と推論【初級 深層学習講座】
XORで学ぶ多層ニューラルネットワークの学習と推論【初級 深層学習講座】

今回は、この調整をSGD（確率的勾配降下法）という最適化手法を使って行います。SGDは、モデルの予測がどれだけ間違っているかを示す「損失（Loss）」という指標を頼りにパラメータを更新します。

このSGDの基本となるのが「勾配降下法」です。これを簡単なグラフで考えてみましょう。 横軸をパラメータx、縦軸を損失yとしたとき、$y=x^2$のような放物線を想像してください。学習の目的は、この放物線の最も低い点（損失が最小になる点）を見つけることです。

放物線グラフ

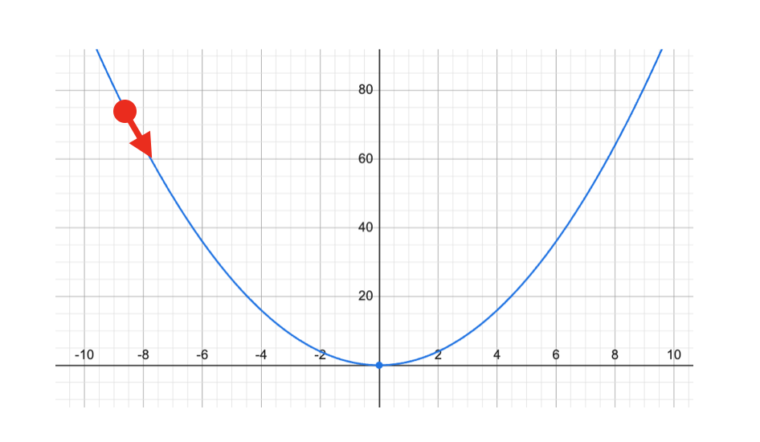
勾配降下法では、まず放物線上のランダムな点（たとえば図の赤点）からスタートします。そして、その点の「傾き（勾配）」を計算します。もし傾きがマイナスなら、谷は右側にあるのでxを少し大きくします。もし傾きがプラスなら、谷は左側にあるのでxを少し小さくします。この「傾きを見て、谷の方向へ少し下りる」というステップを繰り返すことで、最終的に放物線の底にたどり着くことができます。

少しずつ補正する点がポイントです。xを一気に動かすと、最小点を通り過ぎてしまいます。上の例は簡単な放物線ですが、実際の学習は、複雑な関数で最小点を探索する問題になります。

今回使う確率的勾配降下法（SGD）は、この考え方を基本としつつ、ステップごとに確率的に勾配を進めます。時には損失が高い方へ移動することもありますが、全体としては谷底へ向かって進んでいきます。確率的に一時的に損失が増える方向へ動くことで、最小値に向かうことができるというメリットがあります。これにより、山や谷が複数あるような複雑な最小化問題にも対応できます。

この「損失」とは、モデルの出力した予測値と、本来あるべき正解の値とのズレの大きさを表す数値です。単純なイメージとしては、以下のように計算されます。

損失 = |正解の値 - モデルの予測値|

ズレが大きければ損失の値も大きくなり、ズレが小さければ損失も小さくなります。学習の目的は、この損失を最小化することです。今回のANDの学習で使用するBCE Loss（バイナリクロスエントロピー損失）も、この考え方に基づいています。SGDは、計算された損失が最も小さくなる方向（勾配が最も急な坂道）を見つけ、そちらへパラメータを少しずつ動かしていく、というシンプルな手法です。

それでは、実際にPythonとPyTorchを使って、学習の様子を確認していきたいと思います。

ANDの学習モデルを作成し学習させる

まずは、PyTorchを使ってANDゲートを学習するための簡単なモデルを準備します。

ステップ1：ライブラリのインポートと乱数の初期化

はじめに、必要なライブラリをインポートし、毎回同じ結果が得られるように乱数シードを固定します。

import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import japanize_matplotlib

# --- 1. 初期設定 ---
seed = 2025
torch.manual_seed(seed)
np.random.seed(seed)

ステップ2：データとモデルの準備

X, Yは入力の0/1パターンと、それぞれに対応するANDの真値です。ANDの場合は４パターンしかありませんので、これが学習データとなります。

入力が2つ（x1​,x2​）、出力が1つ（0か1）なので、nn.Linear(2, 1)で線形層を定義します。 次に続くnn.Sigmoid()は活性化関数と呼ばれ、線形層からの出力を0から1の間の「確率」のような値に変換する役割があります。これにより、出力が0.5より大きければ「1（真）」、小さければ「0（偽）」といった判断がしやすくなります。


# --- 2. データとモデルの準備 ---
X = torch.tensor([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]], dtype=torch.float32)
y = torch.tensor([[0.0], [0.0], [0.0], [1.0]], dtype=torch.float32)
model = nn.Sequential(nn.Linear(2, 1), nn.Sigmoid())

loss_fn = nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.5)

with torch.no_grad():
    model[0].weight.data = torch.tensor([[-1.0, 1.0]])
    model[0].bias.data = torch.tensor([0.0])

loss_fnは損失関数、optimizerは最適化手法を定義しています。最適化手法は先ほど説明したSGDです。

with torch.no_grad()以降のコードは、$w_1, w_2, b$の初期値を設定です。今回は、それぞれ-1, 1, 0に設定しています。

ステップ3：学習の実行

定義したモデルとデータを使って実際に訓練を行います。ここでは1000回（epochs）の学習を繰り返し、その過程でパラメータと損失がどう変化したかを記録しておきます。

学習ループの中では、以下の処理が繰り返されます。

  1. y_pred = model(X)：現在のモデルで予測値を計算します。
  2. loss = loss_fn(y_pred, y)：予測値と正解ラベルを比べ、損失（ズレの大きさ）を計算します。
  3. optimizer.zero_grad()：前回の計算結果が残らないように、勾配をリセットします。
  4. loss.backward()：逆伝播の心臓部です。 損失に対して各パラメータがどれだけ影響を与えたか（勾配）を自動で計算します。
  5. optimizer.step()：計算された勾配を基に、損失が小さくなる方向へパラメータを少しずつ更新します。

コードの他の部分は、可視化のためのパラメータの保存処理になります。

# --- 3. 学習の実行と過程の記録 ---
epochs = 1000
param_history = []
loss_history = []
w_initial = model[0].weight.detach().clone().numpy().flatten()
b_initial = model[0].bias.detach().clone().numpy().flatten()

model.train()
losses = []
for epoch in range(epochs):
    y_pred = model(X)
    loss = loss_fn(y_pred, y)
    loss_history.append(loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    w = model[0].weight.detach().numpy().flatten()
    b = model[0].bias.detach().numpy().flatten()
    param_history.append(np.concatenate((w, b)))
    losses.append(loss.item())
    
w_final = model[0].weight.detach().clone().numpy().flatten()
b_final = model[0].bias.detach().clone().numpy().flatten()

学習後のモデルは、ANDゲートの入力を正しく分類できるようになっているはずです。実際に予測を行うと以下のような結果になります。

# --- 4. 学習後のモデルパラメータを取得し、可視化
# モデルを評価モードに設定
model.eval()
result = model(X).detach().squeeze(-1).numpy()
print("X1 X2 RESULT")
for [x1, x2], res in zip(X, result) :
    print(f"{x1.item():.0f} & {x2.item():.0f} = {round(res)} ({res:.2f})")
学習後のモデルの出力
X1 X2 RESULT
0 & 0 = 0 (0.00)
0 & 1 = 0 (0.04)
1 & 0 = 0 (0.04)
1 & 1 = 1 (0.94)

では、この学習プロセスで内部的に何が起こっていたのかを、グラフで見ていきましょう。

学習過程を可視化する

ここからが本題です。先ほど記録した学習の履歴を使って、パラメータがどのように最適化されていったのかを4つのグラフで可視化します。

グラフ1: 境界線の変化

このグラフは、学習によってモデルが引く「境界線」がどのように変化したかを示しています。

  • 点: 青い丸（o）が「偽（0）」、オレンジのバツ（x）が「真（1）」のデータ点です。
  • 緑の線: 学習開始時のパラメータが作る初期の境界線です。この時点では、データを全く正しく分離できていません。
  • 赤の線: 1000回のエポックを経て学習が完了した後の最終的な境界線です。oとxをきれいに分割する線に変化していることがわかります。
境界の変化

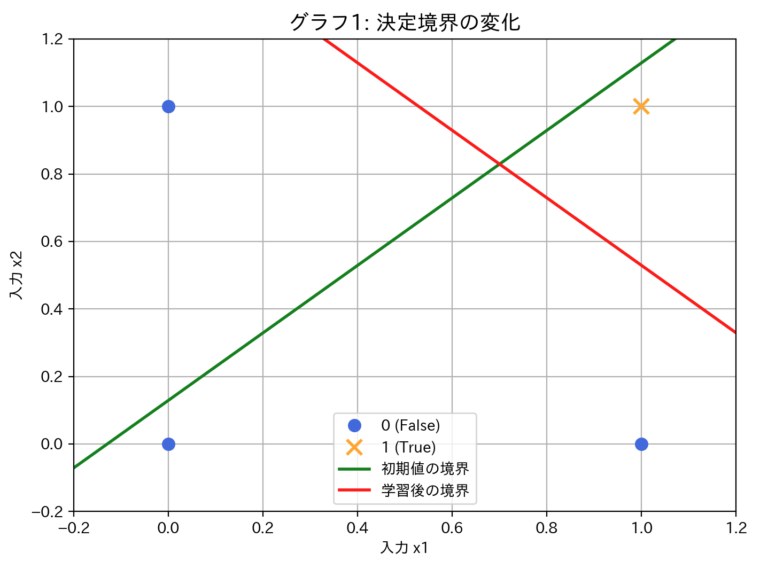
逆伝播による学習は、この緑の線を少しずつ動かし、データを最もよく分離できる赤い線の位置へと最適化していくプロセスになります。

グラフ2: パラメータの学習による変化

次に、境界線を動かしていたパラメータ（w1​,w2​,b）自身の変化を見てみましょう。

  • 横軸: エポック数（学習回数）
  • 縦軸: 各パラメータの値
パラメータの変化

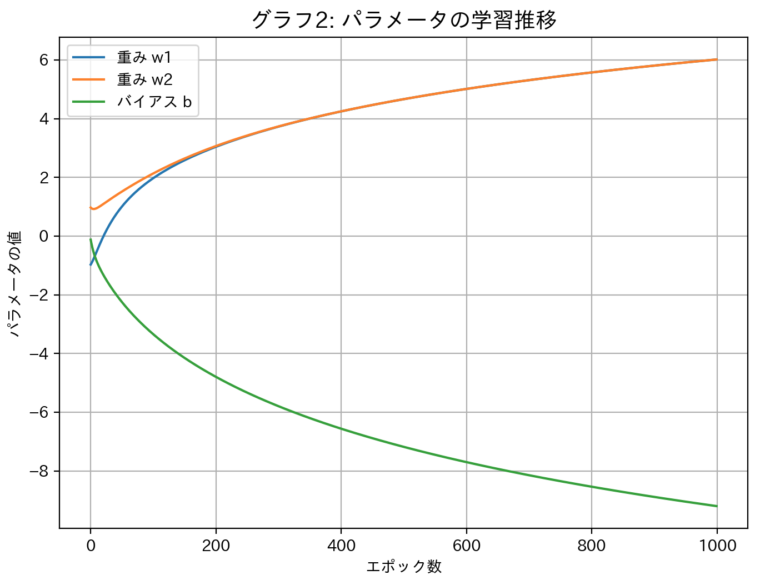
学習開始直後は大きく変動していますが、学習が進むにつれて徐々に変動が小さくなり、最終的にはある特定の値に収束していく様子がはっきりと見て取れます。これは、SGDが「損失」という指標を頼りに、最適なパラメータ値を探索し、見つけ出すまでの過程を表現しています。

グラフ3 & 4: 損失曲面と学習経路

最後に、学習プロセスをより立体的に理解するために「損失曲面」を見てみましょう。これは、パラメータ (w1​,w2​) の組み合わせに対して、損失の値がどのように分布しているか等高線で表現したものです（計算を簡単にするため、バイアスbは学習後の値に固定しています）。

ここでの等高線は、同じ損失値を同じ高さとして表現したものです。

グラフ3: 損失曲面 (2D等高線) と学習経路

  • 色の濃淡: 地図の等高線のように、損失の値を色で表しています。紫の部分が「谷底」で損失が最も低く、黄色に近づくほど損失が高くなります。
  • 白い星印: 学習のスタート地点です。
  • 黒いX印: 学習のゴール地点（最終的なパラメータ）です。
  • 赤い線: スタートからゴールまで、パラメータが移動した経路です。
損失曲面（2D）

このグラフから、パラメータが損失の高い場所から、まるで坂道を転がり落ちるように最も低い「谷底」へと向かっていく様子がわかります。SGD（勾配降下法）という名前の通り、まさに勾配を下っているわけです。

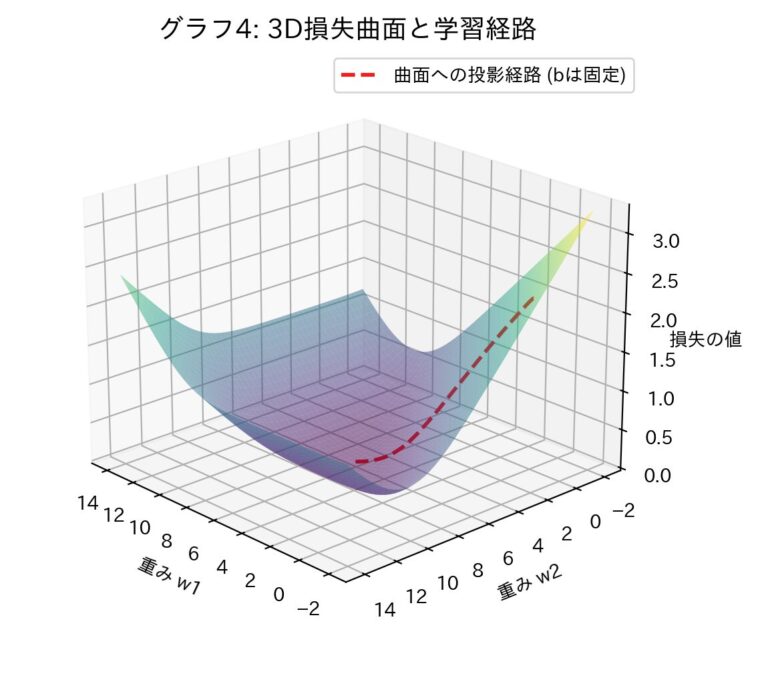
グラフ4: 3D損失曲面と学習経路

グラフ3を3Dで表示したものです。パラメータの学習経路（赤い点線）が、お椀のような形をした曲面の斜面を下っていく様子がより立体的に捉えられます。逆伝播とは、この「損失の地形」における現在地の傾き（勾配）を計算し、パラメータを谷底の方向へ一歩進める、という処理を繰り返しているのです。

損失曲面（3D）

全プログラムリスト

以下、今回使った全プログラムリストです。自身で動かしてグラフを作成することができます。興味のある方はトライしてみてください。

import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import japanize_matplotlib

# --- 1. 初期設定 ---
seed = 2025
torch.manual_seed(seed)
np.random.seed(seed)

# --- 2. データとモデルの準備 ---
X = torch.tensor([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]], dtype=torch.float32)
y = torch.tensor([[0.0], [0.0], [0.0], [1.0]], dtype=torch.float32)
model = nn.Sequential(nn.Linear(2, 1), nn.Sigmoid())
loss_fn = nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.5)

with torch.no_grad():
    model[0].weight.data = torch.tensor([[-1.0, 1.0]])
    model[0].bias.data = torch.tensor([0.0])

# --- 3. 学習の実行と過程の記録 ---
epochs = 1000
param_history = []
loss_history = []
w_initial = model[0].weight.detach().clone().numpy().flatten()
b_initial = model[0].bias.detach().clone().numpy().flatten()

model.train()
losses = []
for epoch in range(epochs):
    y_pred = model(X)
    loss = loss_fn(y_pred, y)
    loss_history.append(loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    w = model[0].weight.detach().numpy().flatten()
    b = model[0].bias.detach().numpy().flatten()
    param_history.append(np.concatenate((w, b)))
    losses.append(loss.item())
    
w_final = model[0].weight.detach().clone().numpy().flatten()
b_final = model[0].bias.detach().clone().numpy().flatten()

plt.plot(losses)
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Training Loss for AND Problem")
plt.show()


# --- 4. 学習後のモデルパラメータを取得し、可視化
# モデルを評価モードに設定
model.eval()
result = model(X).detach().squeeze(-1).numpy()
print("X1 X2 RESULT")
for [x1, x2], res in zip(X, result) :
    print(f"{x1.item():.0f} & {x2.item():.0f} = {round(res)} ({res:.2f})")


# --- 5. 視覚化 ---
fig = plt.figure(figsize=(14, 12))
fig.suptitle("SGDによる学習過程の可視化 (ANDゲート)", fontsize=20)

# --- グラフ1: 決定境界の変化（修正版） ---
ax1 = fig.add_subplot(2, 2, 1)
ax1.set_title("グラフ1: 決定境界の変化", fontsize=14)
ax1.plot(X.numpy()[y.flatten() == 0, 0], X.numpy()[y.flatten() == 0, 1], 'o', c='royalblue', markersize=8, label='0 (False)')
ax1.plot(X.numpy()[y.flatten() == 1, 0], X.numpy()[y.flatten() == 1, 1], 'x', c='orange', markersize=10, mew=2, label='1 (True)')

x1_boundary = np.array([-0.2, 1.2])

# 初期値の決定境界を破線で描画
w1, w2, b = param_history[0][0], param_history[0][1], param_history[0][2]
x2_boundary_start = -(w1 * x1_boundary + b) / w2
ax1.plot(x1_boundary, x2_boundary_start, color="green", linewidth=2, label='初期値の境界')

# 最終的な決定境界を太線で描画
w1, w2, b = w_final[0], w_final[1], b_final[0]
x2_boundary_final = -(w1 * x1_boundary + b) / w2
ax1.plot(x1_boundary, x2_boundary_final, color="red", linewidth=2, label='学習後の境界')

ax1.set_xlabel("入力 x1")
ax1.set_ylabel("入力 x2")
ax1.set_xlim(-0.2, 1.2)
ax1.set_ylim(-0.2, 1.2)
ax1.legend()
ax1.grid(True)


# --- グラフ2: パラメータの学習推移 ---
ax2 = fig.add_subplot(2, 2, 2)
param_history_np = np.array(param_history)
ax2.plot(param_history_np[:, 0], label='重み w1')
ax2.plot(param_history_np[:, 1], label='重み w2')
ax2.plot(param_history_np[:, 2], label='バイアス b')
ax2.set_title("グラフ2: パラメータの学習推移", fontsize=14)
ax2.set_xlabel("エポック数")
ax2.set_ylabel("パラメータの値")
ax2.legend()
ax2.grid(True)

# --- 損失曲面の計算 (グラフ3, 4で共通利用) ---
w1_range = np.linspace(w_final[0] - 8, w_final[0] + 8, 50)
w2_range = np.linspace(w_final[1] - 8, w_final[1] + 8, 50)
W1, W2 = np.meshgrid(w1_range, w2_range)
loss_surface = np.zeros_like(W1)
temp_model = nn.Sequential(nn.Linear(2,1), nn.Sigmoid())
temp_model[0].bias.data = torch.tensor(b_final, dtype=torch.float32)

for i in range(W1.shape[0]):
    for j in range(W1.shape[1]):
        temp_model[0].weight.data = torch.tensor([[W1[i, j], W2[i, j]]], dtype=torch.float32)
        loss_surface[i, j] = loss_fn(temp_model(X), y).item()

# --- グラフ3: 損失曲面 (2D等高線) ---
ax3 = fig.add_subplot(2, 2, 3)
ax3.set_title("グラフ3: 損失曲面 (2D等高線) と学習経路", fontsize=14)
contour = ax3.contourf(W1, W2, loss_surface, levels=30, cmap='viridis', alpha=0.8)
fig.colorbar(contour, ax=ax3, label='損失の値 (bは最終値に固定)')
ax3.plot(param_history_np[:, 0], param_history_np[:, 1], 'r-o', markersize=3, linewidth=1, label='学習経路')
ax3.plot(w_initial[0], w_initial[1], 'white', marker='*', markersize=15, label='開始点')
ax3.plot(w_final[0], w_final[1], 'black', marker='X', markersize=15, label='最終点')
ax3.set_xlabel("重み w1")
ax3.set_ylabel("重み w2")
ax3.legend()

# --- グラフ4: 損失曲面 (3D) と学習経路（修正版） ---
ax4 = fig.add_subplot(2, 2, 4, projection='3d')
ax4.set_title("グラフ4: 3D損失曲面と学習経路", fontsize=14)
ax4.plot_surface(W1, W2, loss_surface, cmap='viridis', alpha=0.5, rstride=1, cstride=1)
path_w1 = param_history_np[:, 0]
path_w2 = param_history_np[:, 1]

projected_loss_path = []
for w1, w2 in zip(path_w1, path_w2):
    temp_model[0].weight.data = torch.tensor([[w1, w2]], dtype=torch.float32)
    projected_loss_path.append(loss_fn(temp_model(X), y).item())
ax4.plot(path_w1, path_w2, projected_loss_path, 'r--', linewidth=2, label='曲面への投影経路 (bは固定)')
ax4.set_xlabel("重み w1")
ax4.set_ylabel("重み w2")
ax4.set_zlabel("損失の値")
ax4.legend()
ax4.view_init(elev=35, azim=130)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

まとめ

今回は、ANDゲートというシンプルな問題を題材に、逆伝播による学習のプロセスを可視化してみました。

  • 学習とは、データを分離する境界線を最適な位置に動かすこと
  • その境界線はパラメータ(w,b)によって決まる
  • 逆伝播とSGDは、損失曲面という地形の最も低い場所（損失最小）を目指して、パラメータを自動的に更新していく仕組み

これらのグラフを通して、数式だけでは捉えにくかった逆伝播の挙動が、より具体的で直感的なイメージとして理解できたのではないでしょうか。複雑なニューラルネットワークも、基本的にはこの延長線上にあり、より高次元で複雑な「損失の地形」を探索していると考えることができます。

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

ABOUT ME
ある/Aru
ある/Aru
IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)
Contact
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
おすすめ書籍
Recommend
こちらの記事もどうぞ
記事URLをコピーしました