2023.10.03 2024.09.23

記事内に商品プロモーションを含む場合があります

Go言語でUnionFind（DSU）を実装｜データ構造とアルゴリズム

Aru

UnionFind（Disjoint Set Union, DSU）は、よく知られるデータ構造・アルゴリズムの１つです。AtCoderなどの競技プログラミングでは頻繁に利用されるだけでなく、実務でのグループ分けなどに使われることがあります。本記事では、Go言語を使ってUnionFindを実装する方法を、データ構造を含めて解説します。

AtCoder関連の記事は以下

AtCoderで役立つ記事一覧（Python, Go言語）

Contents

UnionFind（素集合データ構造）
応用例（どういうところで使うの？）
実装
使い方
参考：コード全体

UnionFind（素集合データ構造）

UnionFind（または、DSU, Disjoint Set Union）と呼ばれるデータ構造は、データの集合を素集合に分割して管理するデータ構造です（WikiPediaを参照）。

このデータ構造を使うと、「ある要素XとYが同じ集合に含まれているか？」「要素Xと同じ集合に含まれている要素の個数」などを高速に求めることが可能です。

このデータ構造に対する基本操作は以下になります

Merge(x, y)
Union(x,y)と書くこともあります。xを含む集合と、yを含む集合を統合して１つの集合する処理です。Merge(x, y)とMerge(y, z)を行うと、xとzは同じ集合に含まれるようになるのが特徴です。このように集合の結合を行うのがMergeです。
Leader(X)
Find(X)と書くこともあります。Xを含む集合の代表の要素を返します。同じ集合に含まれる要素であれば、代表の要素の値は同じになります。グラフとして考えると、これは根（Root）になります。

また、これ以外に以下の操作を用意することもあります。

Same(X, Y)
要素X,Yが同じ集合に含まれているかどうかをtrue, falseで返します
Size(X)
要素Xが含まれる集合の要素数を返します。１の場合は、孤立していることになります。
Groups()
各グループに含まれる要素を列挙します

応用例（どういうところで使うの？）

たとえば、「AさんとBさんが友達」というたくさんの情報から、友人繋がりのあるグループを調べるとか、そういうことに使えます。

また、距離が閾値以下の点だけ繋げた時に、閾値以下の距離の点を経由して到達できる集合を調べることができます。

データ分析・解析でも、「AとBの直接の関係が記述されていない時に、２つが同じグループに含まれているか」というチェックは結構頻出です。これを高速に行うことができるUnion-Findは知っておくと重宝します。

Kaggleとかだと、実行制限時間があるので、これを使って高速化すれば、その分他の処理ができるようになり有利になったりします。

実装

UnionFindをGo言語で実装します。Go言語にはクラスはありませんが、構造体とメソッドを使ってオブジェクト指向のような機能を実現できます。以下は、その実装例です。

実装ではUnionFindではなく、DSUとしています。AtCoderのライブラリに合わせた形です。

データ構造

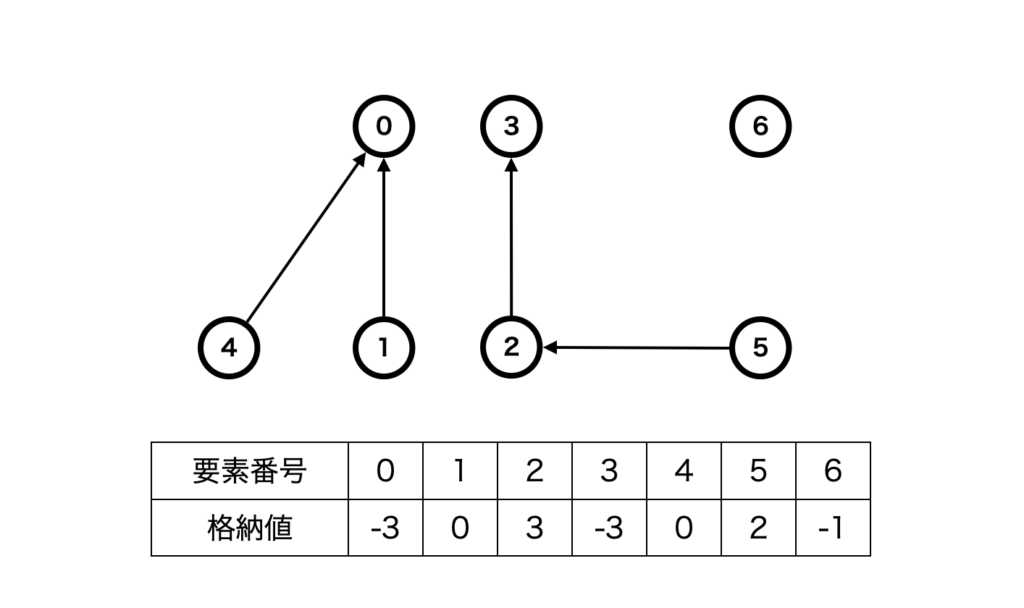
以下の図はデータ構造をグラフで表現したものです。

UnionFindのデータの実態は、配列です。例ではノードが7個あるので、要素数が7の配列となります。親となる要素の番号を管理する配列と、ノード数を管理する配列を別々に用意しても良いですが、要素の値が負の場合は集合の代表要素であり、その値は要素数を表すとします。一方、正の場合は親ノードの番号を示すように実装すれば、１つの配列で両方を管理できるようになります。

下図では、要素0, 1, 4が同じ集合に、2, 3, 5が同じ集合に、そして6が単独の要素の場合の配列の内容の例です。集合の代表要素となる要素0, 3, 6には、それぞれの集合の要素数が格納されています（負数として）。他のノードは親のノードの要素番号が格納されています。

以下では、このような配列を生成するコードを実装します。

初期化

親ノードまたは、集合のサイズを管理する配列と、要素数を管理する変数を構造体として準備します。

type DSU struct {
	parentOrSize []int
	n            int
}

以下は、新たにUnionFindの構造体を生成する関数です。UnionFindを使う場合は、まず、この関数を呼び出して初期化された構造体を生成します。

NewDSUの引数は、要素数nです。最初は、すべての要素は別々の集合なので、配列は-1に初期化しておきます。こうすることで、それぞれが１個だけの集合だと定義されます。

func NewDsu(n int) *DSU {
	var d DSU
	d.n = n
	d.parentOrSize = make([]int, n)
	for i := 0; i < n; i++ {
		d.parentOrSize[i] = -1
	}
	return &d
}

Leader

集合の代表要素の番号を返す関数です。配列の要素の値が負数になるまで再起的に呼び出せば、代表要素の番号を返すことができます。

// Leader :
func (d DSU) Leader(a int) int {
	if d.parentOrSize[a] < 0 {
		return a
	}
	d.parentOrSize[a] = d.Leader(d.parentOrSize[a])
	return d.parentOrSize[a]
}

Merge

集合aとbを結合する関数です。それぞれの集合の代表を調べて、片方を反対側の集合に繋げます。これで全体が１つの集合となります。サイズ比較してどちらを親にするか決める処理が入っていますが、これは、深さを小さくするためのテクニックです。


// Merge :
func (d DSU) Merge(a, b int) int {
	x, y := d.Leader(a), d.Leader(b)
	if x == y {
		return x
	}
	if -d.parentOrSize[x] < -d.parentOrSize[y] {
		x, y = y, x
	}
	d.parentOrSize[x] += d.parentOrSize[y]
	d.parentOrSize[y] = x
	return x
}

Same

要素aとbの代表要素が同じかどうか調べて返すだけです。

// Same :
func (d DSU) Same(a, b int) bool {
	return d.Leader(a) == d.Leader(b)
}

Size

要素数を返すSizeもLeaderが実装できていれば簡単に実装することができます。

// Size :
func (d DSU) Size(a int) int {
	return -d.parentOrSize[d.Leader(a)]
}

Groups

どの要素番号が親になるかわからないので（小さい要素番号が親になっているとは限らない）、一度mapを使って、それぞれの要素が代表要素の集合に含まれるかを調べ、その結果を改めて配列に変換しています。

mapのままでよければ、後半の処理は必要ありません（無駄と言えば無駄ですが、ACLのフォーマットに合わせた形です）。

func (d DSU) Groups() [][]int {
	m := make(map[int][]int)
	for i := 0; i < d.n; i++ {
		x := d.Leader(i)
		if x < 0 {
			m[i] = append(m[i], i)
		} else {
			m[x] = append(m[x], i)
		}
	}
	ret := make([][]int, len(m))
	idx := 0
	for _, e := range m {
		ret[idx] = make([]int, len(e))
		copy(ret[idx], e)
		idx++
	}
	return ret
}

使い方

以下のような使い方をします。

func main() {
	uf := NewDsu(10)
	uf.Merge(0, 1)
	uf.Merge(1, 2)
	uf.Merge(5, 6)
	fmt.Println(uf.Same(0, 2))
	fmt.Println(uf.Same(0, 5))
	fmt.Println(uf.Groups())
}

出力結果

true
false
[[5 6] [7] [8] [9] [0 1 2] [3] [4]]

参考：コード全体

以下に、コード全体をつけておきます。テンプレ的に使ってもらってもOKです。

AtCoderのコンテストで何度も使っているコードですので、動作は問題ないと思います。

//
// Disjoint Set Union: Union Find Tree
//

// DSU :
type DSU struct {
	parentOrSize []int
	n            int
}

// NewDsu :
func NewDsu(n int) *DSU {
	var d DSU
	d.n = n
	d.parentOrSize = make([]int, n)
	for i := 0; i < n; i++ {
		d.parentOrSize[i] = -1
	}
	return &d
}

// Merge :
func (d DSU) Merge(a, b int) int {
	x, y := d.Leader(a), d.Leader(b)
	if x == y {
		return x
	}
	if -d.parentOrSize[x] < -d.parentOrSize[y] {
		x, y = y, x
	}
	d.parentOrSize[x] += d.parentOrSize[y]
	d.parentOrSize[y] = x
	return x
}

// Same :
func (d DSU) Same(a, b int) bool {
	return d.Leader(a) == d.Leader(b)
}

// Leader :
func (d DSU) Leader(a int) int {
	if d.parentOrSize[a] < 0 {
		return a
	}
	d.parentOrSize[a] = d.Leader(d.parentOrSize[a])
	return d.parentOrSize[a]
}

// Size :
func (d DSU) Size(a int) int {
	return -d.parentOrSize[d.Leader(a)]
}

// Groups :
func (d DSU) Groups() [][]int {
	m := make(map[int][]int)
	for i := 0; i < d.n; i++ {
		x := d.Leader(i)
		if x < 0 {
			m[i] = append(m[i], i)
		} else {
			m[x] = append(m[x], i)
		}
	}
	ret := make([][]int, len(m))
	idx := 0
	for _, e := range m {
		ret[idx] = make([]int, len(e))
		copy(ret[idx], e)
		idx++
	}
	return ret
}

#Golang #Go言語 #UnionFind