2024.11.07

記事内に商品プロモーションを含む場合があります

深層学習の指標Perplexityを解説【初級深層学習講座】

Aru

この記事では、Perplexity（パープレキシティ）という深層学習や言語モデルの評価指標について解説します。Perplexityは、モデルがどれだけ正確に次のトークンを予測できるかを示す指標です。本記事では、Perplexityの基本的な計算方法、解釈、そして具体的な例を通して、なぜこの指標が重要なのかを詳しく説明します。

Contents

Perplexityの解説
画像のクラス分類におけるPerplexityの応用
まとめ

Perplexityの解説

以下、自然言語処理におけるPerplexityについて解説します。

Perplexityとは

Perplexity（パープレキシティ）は、主に自然言語処理において、言語モデルがどれだけうまく次の単語（トークン）を予測できるかを測定するために使用される指標です。

具体的には、モデルが予測する次のトークンの不確実性を数値化したもので、Perplexityの値が小さいほどモデルが高精度に次のトークンを予測できていることを意味します。

Perplexityは小さいほど良い指標です。

Perplexityの数式と計算方法

Perplexityは、次の数式で計算されます：

Perplexityの数式

$$Perplexity=\exp⁡ \Bigl( −\frac{1}{N}\sum_{i=1}^{N}\log ⁡P(w_i) \Bigr)$$

ここで、

$N$ はテストデータ内のトークン数、
$P(w_i)$ はモデルが予測したトークン $w_i$ の確率です。

解説では、$\log$は、$\log_e$（$\ln$）です。

この数式は、モデルが予測した各トークンの確率の対数を平均し、その指数をとることで計算されます。結果的に、Perplexityは「次のトークンが正解である確率の逆数」として理解することが可能です。

Perplexityの直感的な意味

Perplexityは、ある種の不確実性の指標です。たとえば、Perplexityが10の場合、モデルは次のトークンを予測する際に、語彙全体の中で平均して上位10個の選択肢の中に正解が含まれていると解釈できます。

選択肢の数は少ない方が良いので、Perplexityが低いほどモデルがより正確に次のトークンを予測していること意味します。

Perplexityの数値を直感的に捉える場合は、この考え方が良いかと思います

Perplexityを用いたモデル評価

Perplexityはモデルの評価指標として重要です。

特に、以下のケースで評価値として利用できます。

モデルの精度を評価
Perplexityが低ければ低いほどモデルはトークンを正確に予測できていることを評価値として利用する
異なるモデルの比較
同じテストデータに対して異なるモデルのPerplexityを比較することで、どのモデルが優れているかの評価に利用する

具体例

ここでは、具体的にPerplexityを計算してみます。

ここでは、テストデータとして “This is a test.” という短い文章を使用し、次のように単語単位でトークン化されたとします。

“This”
“is”
“a”
“test”
“.”

したがって、トークン数は5です。

また、各トークンに対する条件付き確率が次のように与えられていると仮定します：

$P(\text{“is”} | \text{“This”}) = 0.3$
$P(\text{“a”} | \text{“This is”}) = 0.4$
$P(\text{“test”} | \text{“This is a”}) = 0.2$
$P(\text{“.”} | \text{“This is a test”}) = 0.1$

これらの値を使ってPerplexityを計算してみます。

条件付き確率のイメージ

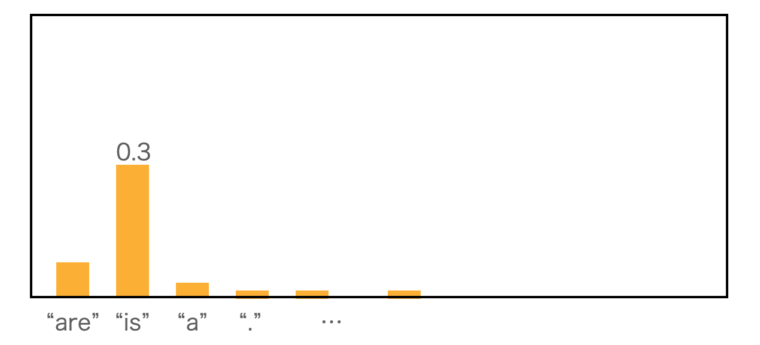
条件付き確率$P(\text{“is”} | \text{“This”}) = 0.3$のイメージは以下のようになります。各語彙の確率が次のように与えられているとした時に、”is”が来る確率が0.3なので0.3となります。下記の例では、”are”や”a”などにも一定の確率が与えられています。正解は”is”なので”is”の確率0.3が採用されて結果になります。

まず、各確率の対数を取り、その平均を計算します。

各トークンの条件付き確率を掛け合わせて、全体の確率を求めます。

$$
P(w_1, w_2, w_3, w_4, w_5) = P(w_2 | w_1) \cdot P(w_3 | w_1, w_2) \cdot P(w_4 | w_1, w_2, w_3) \cdot P(w_5 | w_1, w_2, w_3, w_4)
$$

これに基づいて計算を行います。

$$
P(w_1, w_2, w_3, w_4, w_5) = 0.3 \cdot 0.4 \cdot 0.2 \cdot 0.1
$$

各ステップでの計算を示します：

$0.3 \cdot 0.4 = 0.12$
$0.12 \cdot 0.2 = 0.024$
$0.024 \cdot 0.1 = 0.0024$

したがって、全体の確率は次のようになります

$$
P(w_1, w_2, w_3, w_4, w_5) = 0.0024
$$

各トークンに対する対数確率の合計を計算します

$$
\begin{align}
\sum_{i=1}^{N} \log P(w_i | \text{context}) = & \log P(w_2 | w_1) + \\
& \log P(w_3 | w_1, w_2) + \\
&\log P(w_4 | w_1, w_2, w_3) + \\
&\log P(w_5 | w_1, w_2, w_3, w_4)
\end{align}
$$

計算を行います：

$\log P(w_2 | w_1) = \log(0.3) \approx -1.203$
$\log P(w_3 | w_1, w_2) = \log(0.4) \approx -0.916$
$\log P(w_4 | w_1, w_2, w_3) = \log(0.2) \approx -1.609$
$\log P(w_5 | w_1, w_2, w_3, w_4) = \log(0.1) \approx -2.303$

これらを合計します
$$
-1.203 – 0.916 – 1.609 – 2.303 \approx -6.031
$$

これを用いて Perplexity を計算します

$$\text{Perplexity} = \exp\left(-\frac{1}{5} \cdot (-6.031)\right) = \exp\left(\frac{6.031}{5}\right) = \exp(1.2062) \approx 3.34$$

この例のテストデータのperplexityは3.34と計算できました。Perplexityの計算イメージは掴めたでしょうか？

Perplexityとモデル性能の関係

基本的にPerplexityは低いほど良いですが、低すぎる場合には過学習の可能性もあるので注意が必要となります。モデルがテストデータに過剰適合すると、Perplexityは低いけど実際のデータ（未知のデータ）に対しては性能が低いということが発生します。Perplexityが低くなるからといって学習回数を増やすことが良い性能につながるわけではないことに注意が必要です。

画像のクラス分類におけるPerplexityの応用

Perplexityは主に自然言語処理（NLP）で使われる評価指標ですが、画像のクラス分類でも似たような考え方を応用できます。画像のクラス分類では、モデルが各クラスに対して予測確率を出力し、その正確性を評価するためにクロスエントロピー損失が一般的に使われます。しかし、Perplexityの概念を適用すると、モデルがクラスをどれだけ「混乱」しているかを測る一つの指標として考えられます。

画像分類におけるPerplexityの計算

画像のクラス分類において、各画像は特定のクラスに属します。たとえば、猫と犬の2クラス分類を考えてみましょう。モデルは、各クラスに対して確率 $P(\text{class} | \text{image})$を出力します。

もしモデルが画像を「猫」として予測する場合、次のような確率を出すことが考えられます：$$
\begin{align}
P(\text{猫} | \text{image}) = 0.7\\
P(\text{犬} | \text{image}) = 0.3
\end{align}$$

この場合、クロスエントロピー損失を基に計算されたPerplexityは次のように表せます

$$
\text{Perplexity} = \exp \left( -\sum_{i=1}^{N} P(\text{true class}_i) \log P(\text{predicted class}_i) \right)
$$

Perplexityが低い場合、モデルはほぼ確実に正しいクラスを予測していることを意味し、Perplexityが高い場合、モデルが複数のクラスの間で混乱していることを示します。

クラス分類でのPerplexity

例えば、ある画像に対して「猫」と「犬」のどちらかを予測する際に、Perplexityが高いということは、モデルが正解クラスの確率を十分に高く予測できず、その他のクラスの確率もそれなりに高くなっていることを意味します。逆に、Perplexityが低い場合、正解クラスの確率が高く、他のクラスは低い確率になっていることを示しています。このあたりは他の指標と似ています。

Perplexityとクロスエントロピーの違い

画像分類で一般的に使われるのはクロスエントロピー損失です。これは予測がどれだけ正確かを数値で評価する指標です。

Perplexityは、クロスエントロピー損失と似た意味になりますが、逆数をとってモデルの「混乱度合い」を表現する点が異なります。

複数クラス分類や多クラス画像認識タスクで、モデルの予測の精度を示す補助的な指標としてりようすることも可能です。

無理に使う必要はないですがPerplexityは自然言語だけでなく、画像のクラス分類などの他の指標としても使えることを覚えておきましょう。

クロスエントロピーはトークンの種類（語彙数）などの影響を受けやすいため自然言語処理ではPerplexityが利用されることが多いようです。個人的見解ですが、画像のクラス分類であまり使われない理由は、そこまで考慮する必要性が少ないからということだと思います。

まとめ

Perplexityは、言語モデルの評価で使われる指標で、モデルが次のトークンをどれだけ正確に予測できるかを示します。直感的にはモデルが次のトークンを選択する際にどの程度の単語から選択しているかを表す指標で、これが少ないほど精度良く選択できていることを示します。

#LLM #ディープラーニング #機械学習

深層学習の指標Perplexityを解説【初級深層学習講座】