【Python】区間の重複を判定する3つの方法(累積和・ソート・座標圧縮)
予定が複数与えられている場合に、ダブルブッキングがないかをプログラムでチェックする方法を解説します。言い換えると、開始時刻と終了時刻の組みが複数与えられた場合に、期間に重複がないかチェックするアルゴリズムになります。これは、 スケジュール管理機能や予約システムなどでよく遭遇する問題ですが、アプローチによって計算量やメモリ効率が変わってきます。この記事では、代表的な2つの解法と、さらに応用的な解法1つを紹介します。
重複チェック(問題の概要)
N個の開始時刻と終了時刻のペアが与えられた場合に、これらの期間に少しでも重なり(重複する部分)がないかチェックする
上記のように、問題は非常にシンプルです。 例えば、2つの予定があり、1つが 10:00-13:00 で、別の予定が 12:30-14:00 だったとします。この場合、12:30から13:00までの30分間が重なっているため、システムは「重複あり」と判定するというものです。
なお、この問題では、単純な重なりだけでなく、片方の期間がもう片方を完全に包含しているケースや、開始時刻と終了時刻がぴったり一致する場合(境界値)の扱いなど、正確に判定するためには考慮すべきエッジケースがいくも存在しますので、適当に実装すると大変になります。
この種の問題は、IT企業の採用時のコーディング試験や、AtCoderなどの競技プログラミングコンテストで頻出する「区間スケジューリング問題」の基礎となるものです。アルゴリズムに慣れているプログラマであれば、サクッと効率的に実装できますが、慣れていないうちは二重ループを使った非効率な方法(計算量が $O(N^2)$)で実装してしまい、大量のデータを処理する際にタイムアウトしてしまったり、複雑なif文の条件分岐でバグを生んでしまったりと、意外に苦戦するポイントでもあります。

この問題、会議室予約システムの実装などで必要になりますので、競プロの問題といいつつ、実務的な部分もあります。
入力データのフォーマット
入力データは、時刻ペアの個数Nが与えられ、続けてN行の開始時刻と終了時刻のペアが与えられるものとします。 時刻は HH:MM のフォーマットになります。
入力例
3
10:00 12:00
11:30 13:00
14:00 15:00
入力データの読み込みと前処理
時刻データのまま比較を行うと扱いづらいため、0:00 からの経過分数(整数値)に変換して管理します。 例えば 10:00 は 10 * 60 + 0 = 600 となります。
まずは、時刻文字列を分(整数)に変換する処理を含め、標準入力からデータを読み込む部分の実装です。
def to_minutes(time_str):
"""HH:MM形式の文字列を0:00からの経過分数(整数)に変換する"""
h, m = map(int, time_str.split(':'))
return h * 60 + m
def get_input() :
n = int(input())
d = []
for i in range(n):
hhmm = input().split()
d.append((to_minutes(hhmm[0]), to_minutes(hhmm[1])))
return d
datas = get_input()
print(datas)get_input()を呼び出すと、開始時刻と終了時刻の組みをタプルとして入力することができます。
解法1:時間を配列にし、累積和を使って管理
この解法は「いもす法」と呼ばれる方法を利用します。 1日分の時間を配列(バケツ)として用意し、開始時刻に +1、終了時刻で -1 を行います。その後、配列の累積和(シミュレーション)をとり、値が 2 以上になる区間があれば「重複している」と判断できます。
この解法は、分単位の配列(24時間なら24*60分=1440分ぶんの配列)を作り、この配列に、それぞれの開始時刻から終了時刻までに「1を足す」という考え方です。ただ、毎回開始時刻〜終了時刻まで1加算すると処理量が大きくなるので、開始時刻に+1を入れ、終了時刻に-1を入れておき、あとでまとめてその範囲に1にする処理を行います。
この後処理は累積和と呼ばれる処理になります。具体的には、配列がa[i+1] += a[i]を計算することで、+1された部分から-1されるまでの区間が全て1で埋め尽くすことができます。また、2つ重なっている部分は2になり、3つ重なっている部分は3になります。この方法では、重なった「数」が計算の過程で分かるという点も便利です。
- メリット
- 実装が直感的でわかりやすい。
- 「どの時間帯に何件重なっているか」といった情報も同時に取得できる。
- デメリット
- 時間の範囲が広い場合(例:数年分のUnixタイムスタンプなど)、巨大な配列が必要になりメモリを消費する。
def to_minutes(time_str):
"""HH:MM形式の文字列を0:00からの経過分数(整数)に変換する"""
h, m = map(int, time_str.split(':'))
return h * 60 + m
def get_input() :
n = int(input())
d = []
for i in range(n):
hhmm = input().split()
d.append((to_minutes(hhmm[0]), to_minutes(hhmm[1])))
return d
def solve():
intervals = get_input()
# 1日分の分数は 24 * 60 = 1440分
# 余裕を持って少し大きめに確保(終了時刻の境界考慮)
timeline = [0] * (24 * 60 + 2)
# 開始時刻に+1, 終了時刻に-1を代入
for start, end in intervals:
timeline[start] += 1
timeline[end] -= 1
# 累積和
for i in range(1, len(timeline)) :
timeline[i] += timeline[i-1]
# 重複チェック
is_overlap = False
for val in timeline:
if val > 1:
return True
return False
if __name__ == "__main__":
is_overlap = solve()
if is_overlap:
print("重複あり")
else:
print("重複なし")解法2:開始時刻でソートして、終了時刻を管理する
解法1は、時刻の範囲が大きくなると配列が大きくなりメモリを消費します。 こちらの方法は、区間を開始時刻でソートし、前から順番に見ていく方法です。
「一つ前の区間の終了時刻」よりも「現在の区間の開始時刻」が早ければ、食い込んでいる(重複している)と判定できます。
- メリット
- 座標の範囲(時間の範囲)がどれだけ広くてもメモリ消費量は入力データ数 $N$ に依存するだけなので、省メモリ。
- 計算量はソートの $O(N \log N)$ が支配的で高速。
- デメリット
- ソートが必要(データが未ソートの場合)。
def to_minutes(time_str):
"""HH:MM形式の文字列を0:00からの経過分数(整数)に変換する"""
h, m = map(int, time_str.split(':'))
return h * 60 + m
def get_input() :
n = int(input())
d = []
for i in range(n):
hhmm = input().split()
d.append((to_minutes(hhmm[0]), to_minutes(hhmm[1])))
return d
def solve():
intervals = get_input()
# 開始時刻でソートする
# Pythonのsortはタプルの0番目の要素(開始時刻)で比較してくれる
sorted_intervals = sorted(intervals)
# 比較用:前のスケジュールの終了時刻
# 最初は比較対象がないため、非常に小さい値にしておく
last_end_time = -1
for start, end in sorted_intervals:
# 現在の開始時刻が、前の終了時刻より前なら重複
if start < last_end_time:
return True
# 終了時刻を更新する
# 包含関係(完全に内包されるケース)を考慮し、より遅い終了時刻を採用する。
# 本問題では last_end_time = end で十分だが、一般化のため max を用いている
last_end_time = max(last_end_time, end)
return False
if __name__ == "__main__":
is_overlap = solve()
if is_overlap:
print("重複あり")
else:
print("重複なし")
解法3(高度な解法):座標圧縮と累積和(いもす法)の組み合わせ
解法1の「重なっている数がわかる」という利点と、解法2の「広い範囲にも対応できる」という利点を組み合わせた、より高度なテクニックとして「座標圧縮(Coordinate Compression)」があります。
考え方
解法1の弱点は、例えば 10:00 と 20:00 の間に予約がなくてもその間の配列を用意しなければならないことでした。 座標圧縮では、データとして登場する時刻(開始時刻と終了時刻)だけを集めてリスト化し、それらに番号(ランク)を振り直します。
例えば 10:00-12:00 と 11:30-13:00 というデータがある場合、登場する時刻は 10:00, 11:30, 12:00, 13:00 の4つだけです。これらを小さい順に並べて 0, 1, 2, 3 というインデックスを割り当てます。 そうすれば、本来の時間間隔に関係なく、このインデックスを使った小さな配列(この例ならサイズ4)だけで累積和(いもす法)を行うことができます。
- メリット
- $10^9$ ~$10^18$といった非常に大きな座標や、小数を含む座標であっても、登場する点の数 $2N$ 程度の配列サイズで処理可能です。
- 解法1と同様に累積和を使うため、「最大でいくつの重複があるか」も正確に計算できます。
def to_minutes(time_str):
"""HH:MM形式の文字列を0:00からの経過分数(整数)に変換する"""
h, m = map(int, time_str.split(':'))
return h * 60 + m
def get_input() :
n = int(input())
d = []
for i in range(n):
hhmm = input().split()
d.append((to_minutes(hhmm[0]), to_minutes(hhmm[1])))
return d
def solve():
intervals = get_input()
# 座標圧縮のために、登場する全ての時刻を保持するセット
points = set()
for s, e in intervals:
points.add(s)
points.add(e)
# 1. 座標圧縮: 登場する時刻をソートしてリスト化
sorted_points = sorted(list(points))
# 2. 各時刻がリストの何番目かを引ける辞書を作成
# 例: {600: 0, 690: 1, 720: 2, ...}
idx = {val: i for i, val in enumerate(sorted_points)}
# 3. 圧縮後のサイズで配列を用意
timeline = [0] * len(sorted_points)
for start, end in intervals:
s, e = idx[start], idx[end]
# いもす法: 開始ランクに+1, 終了ランクに-1
timeline[s] += 1
timeline[e] -= 1
# 4. 累積和
for i in range(1, len(timeline)) :
timeline[i] += timeline[i-1]
# 5. チェック
for val in timeline:
if val > 1:
return True
return False
if __name__ == "__main__":
is_overlap = solve()
if is_overlap:
print("重複あり")
else:
print("重複なし")
この手法を使えば、たとえスケジュールが数万年分あろうと、データ件数が少なければ一瞬で計算が終わります。
ポイントとなる座標圧縮はコードの以下の部分です。
# 座標圧縮のために、登場する全ての時刻を保持するセット
points = set()
for s, e in intervals:
points.add(s)
points.add(e)
# 1. 座標圧縮: 登場する時刻をソートしてリスト化
sorted_points = sorted(list(points))
# 2. 各時刻がリストの何番目かを引ける辞書を作成
# 例: {600: 0, 690: 1, 720: 2, ...}
idx = {val: i for i, val in enumerate(sorted_points)}一旦、集合型に開始時刻と終了時刻を格納します。これで重複したデータが削除(正確には1つにまとめられる)されます。set()はソートされていないので、次にリストに戻してソートします。最後に、辞書型(idx)に時刻と配列のインデックスの対応表を格納して終了です。
以降は、この対応表を使って配列の位置を決めます。このようにすることで「出現した値だけを格納する配列」を作ることができます。
ちなみに、この座標圧縮のコードは典型的な書き方ですので、覚えておくとよいでしょう。
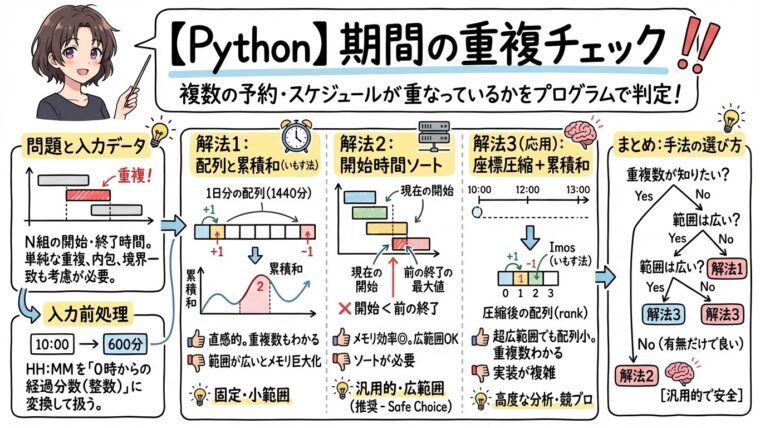
まとめ:手法の選び方
今回紹介した3つの手法は、それぞれ特徴と適したユースケースが異なります。これらを正しく使い分けることで、システムリソースを無駄にせず、かつ保守性の高いコードを書くことができます。
- 解法1(累積和・配列)
- 特徴
配列のインデックスを時刻に見立てるため、直感的に理解しやすく、ロジックのバグが入り込みにくいのが最大の強みです。「何時何分に何人」という状態が配列を見るだけで可視化でき、デバッグも容易です。 - 適したケース
営業時間内(9:00〜18:00)の会議室予約や、映画館の座席管理など、時間の範囲が明確に決まっており、かつそれほど大きくない場合に最適です。 - 付加価値
単なる重複チェックだけでなく、「最大でいくつの重複があるか(最大同時接続数)」や「どの時間帯が混雑しているか」といったヒートマップ的な分析がこの手法一つで行えます。
- 特徴
- 解法2(ソート)
- 特徴
時間の範囲(100年分など)に関わらず、メモリ消費量はデータの件数(N)のみに依存するため、非常に効率的です。予期せぬ未来の日付や過去の日付が入力されても、巨大な配列を作ってしまいメモリ不足(MemoryError)になる心配がありません。 - 適したケース
ユーザーの行動ログ解析、サーバーのアクセスログ、あるいは期間が特定できない汎用的なスケジュール登録機能など。 - 実務での位置付け
計算量、メモリ効率、実装の複雑さのバランスが良く、入力値の制約を気にしなくて済むため、本番システム開発において最も安全かつ汎用的に使える選択肢と言えます。
- 特徴
- 解法3(座標圧縮)
- 特徴
解法1の「重なり数がわかる」メリットと、解法2の「広範囲・疎なデータに強い」メリットを併せ持ちます。ただし、実装工数は増え、インデックス変換の処理が入るため、単純な実装よりもバグが生じやすくなる点に注意が必要です。 - 適したケース
$10^9$〜$10^{18}$といった極端に広い範囲を扱う場合や、秒単位以下の細かい浮動小数点を扱い、かつ重なりの深度(深さ)を知りたい場合。競技プログラミングや、通信トラフィックのピーク解析などの高度なデータ分析で必須のテクニックです。
- 特徴
個人的な指針としては、簡単なツール作成やプロトタイピング、固定範囲のタスクなら解法1、一般的なWebサービスや業務システム開発なら解法2、特殊な要件がある高度な分析やパフォーマンスチューニングが必要なら解法3を選ぶと良いでしょう。「この程度の処理ならどれでやっても同じだろう」と思うかもしれませんが、取り扱うデータ数が「数百万件」などになると、かなり処理時間が変化してきますので、処理量とメモリ量を意識した実装は大切です。





