数列問題｜足して１００以上のパターン数を高速に数える方法（AtCoder向け）
tadanori
Aru's テクログ（Aruaru0）
両端から幅優先探索（BSF）って演算量を削減する｜高速化の手法
tadanori
開始状態と終了状態の双方から幅優先探索を行うことで演算量を削減するテクニックがあります。ここでは、このテクニックを紹介します。
幅優先探索（BSF）
１５パズルなどのパズルゲームを解く場合、次の状態を幅優先探索で検索することで「原理的には」最短手順を求めることが可能です。
下図は、8パズルの例ですが、次の手を探索を揃った状態に到達するまで１手ずつ総当たりで調べていくことで解を見つけることができます。
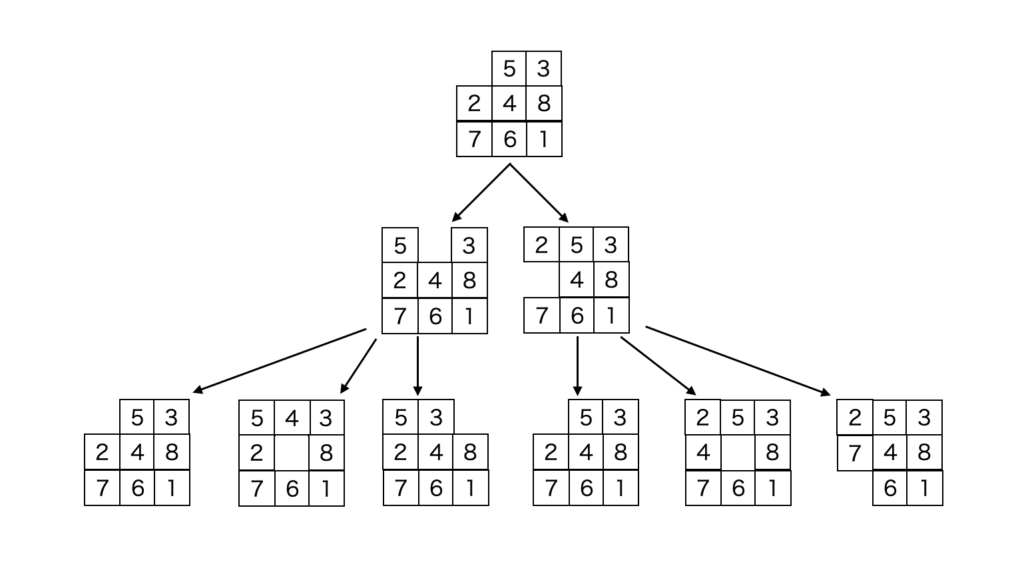
このやり方は、ある深さを探索し終わったら、次の深さを探索するので「幅優先探索」といいます。
原理的にはといったのは、パターンが増えると演算量が爆発して現実的な処理時間では終わらなくなるからです。
例えば、次の状態が２つづある場合、深さ10の場合の状態数は$2^{n}$になります。10手なら1024パターンですが、20手だと1,048,576パターンになります。
このため、ある程度の深さまでしか探索することができません。
探索できる深さを増やすテクニック
パズルの場合、初期状態と目的とする終了状態が分かっています。
初期状態からの探索と同時に、終了状態からの探索を行うとどうなるでしょうか。
下図は８パズルのイメージ図ですが、初期状態から遷移した状態と、終了状態から遷移した状態がどこかで一致するはずです。
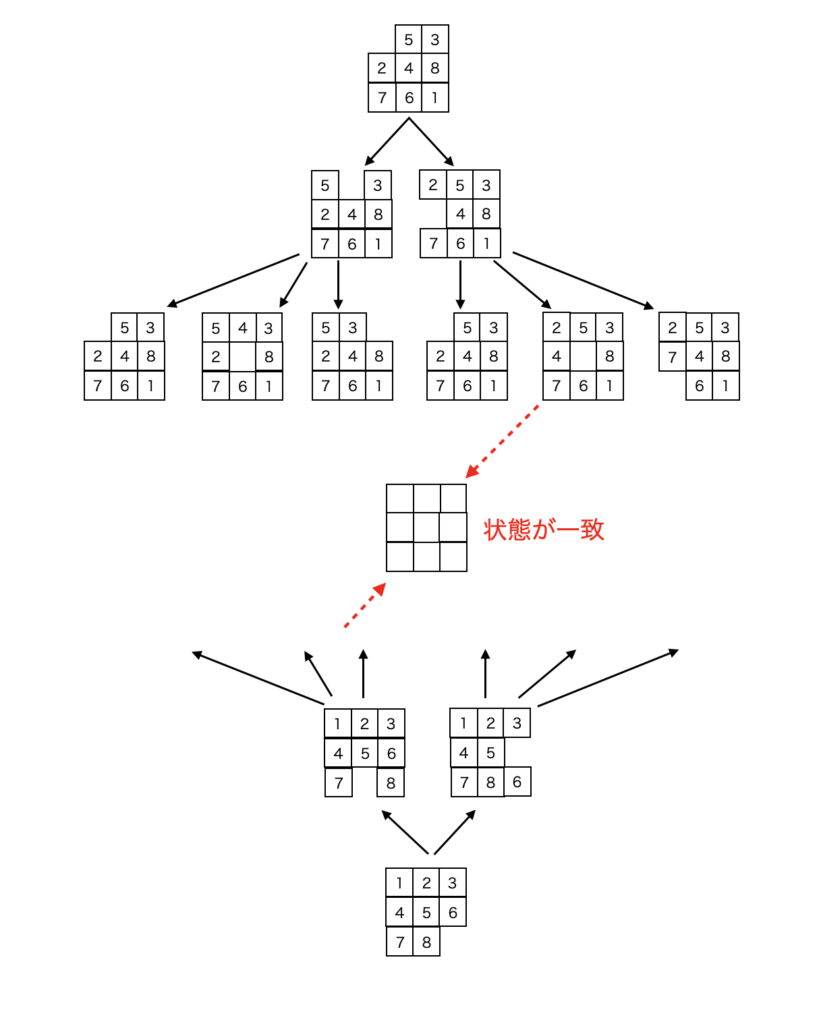
次の状態数が2の場合、10手まで状態遷移させた場合は、初期状態、終了状態からそれぞれ$2^{10}=1024$パターンの2048パターンになります。一方、初期状態からだけ遷移させた場合は、$2^{20}=1,048,576$パターンです。
このように、初期状態と終了状態の双方から探索を行うことで、演算量を削減することができます。
ABC366-F問題を解いてみる（python）
AtCoderのABC366-F問題がちょうど双方向のBSFのサンプルとして良いので、これを利用して解説します。
まずは、コードです。
import hashlib
from collections import deque
def hash(s) :
sha1 = hashlib.sha1()
sha1.update(str(s).encode("utf-8"))
return sha1.hexdigest()
def rot(s, sy, sx) :
nh, nw = H-1, W-1
n = (H - 1) * (W - 1) // 2
cnt = 0
for y in range(nh):
for x in range(nw) :
s[sy+y][sx+x], s[sy+nh-1-y][sx+nw-1-x] = s[sy+nh-1-y][sx+nw-1-x], s[sy+y][sx+x]
cnt+=1
if cnt == n : return s
return s
H, W = map(int, input().split())
s = [list(map(int, input().split())) for _ in range(H)]
t = [[i*W + j + 1 for j in range(W)] for i in range(H)]
# 最初から一致している場合は探索しない
if t == s :
print(0)
exit()
def BSF() :
q0 = deque()
q1 = deque()
q0.append(s)
q1.append(t)
m0 = {hash(s):0}
m1 = {hash(t):0}
for i in range(10) :
tmp0 = deque()
while len(q0) != 0 :
cur = q0.popleft()
cur_h = hash(cur)
for h in range(2):
for w in range(2) :
tmp = [[cur[j][i] for i in range(W)] for j in range(H)]
tmp = rot(tmp, h, w)
hval = hash(tmp)
if hval in m1 : # 見つけた場合
return m0[cur_h]+m1[hval]+1
if hval in m0 : # 既に登録されている状態の場合はスキップ
continue
m0[hval] = m0[cur_h] + 1
tmp0.append(tmp)
tmp1 = deque()
while len(q1) != 0 :
cur = q1.popleft()
cur_h = hash(cur)
for h in range(2):
for w in range(2) :
tmp = [[cur[j][i] for i in range(W)] for j in range(H)]
tmp = rot(tmp, h, w)
hval = hash(tmp)
if hval in m0 : # 見つけた場合
return m0[hval]+m1[cur_h]+1
if hval in m1 : # 既に登録されている状態の場合はスキップ
continue
m1[hval] = m1[cur_h] + 1
tmp1.append(tmp)
q0, q1 = tmp0, tmp1
return -1
ret = BSF()
print(ret)
普通のBSFと異なり、10手で打ち切るようにfor i in range(10)として10手までで終了するようにしています。
これに合わせて、キューに追加するのではなく、tmp0といったテンポラリのキューを作り、次の手はそちらに格納し、ループの度に、q0, q1 = tmp0, tmp1としてキューを書き換えています。
ポイントは、現在の状態を辞書型で保存している部分です。
if hval in m1 : # 見つけた場合
return m0[cur_h]+m1[hval]+1
if hval in m0 : # 既に登録されている状態の場合はスキップ
continue辞書から見つけた場合は、初期状態からの手数と終了状態との手数を合計して返しています。また、既に辞書に登録されている場合はスキップします（同じ状態は遷移させない）。
これを初期状態からと、終了状態からの２つに対して行っています。
この問題では必要ないのですが、辞書のキーはハッシュ関数でハッシュ値に変換して利用しています（sha1を利用）。
def hash(s) :
sha1 = hashlib.sha1()
sha1.update(str(s).encode("utf-8"))
return sha1.hexdigest()ハッシュ値にすることで状態が固定サイズに圧縮できるので、例えば状態が数百バイトになる場合などに、辞書検索を高速化できます。
ハッシュ値は衝突する可能性もあるので注意が必要です
まとめ
最近、パズルの解法を調べていた＆たまたまAtCoderのF問題に双方向BSFが使える問題があったので、解説してみました。
実際に探索する場合にかなり使えるテクニックなので覚えておくと良いかと思います
これに、ルールベースで枝刈りする処理を入れると意外とパズルを解けたりします。
