Binary Indexed Tree（Fenwick Tree）を実装する|Python

競プロでお馴染みのBinary Indexed Tree（BIT, フェニック木）をPythonで実装してみました。高速に累積和を計算、更新できるデータ構造ですが、実装はかなりシンプルです。この記事では、アルゴリズムを丁寧に解説し、Pythonで実装しています。コピペで利用できるコードを用意していますので活用してください。

BIT（Binary Indexed Tree）とは？

BIT（Binary Indexed Tree）は Fenwick Treeとも呼ばれるデータ構造です。

主に、更新が必要な配列の累積和を高速に計算するために使用されます。

BIT は、以下の操作をサポートします：

1. 要素の加算（Add）：指定されたインデックスの要素に値を加算します
2. 累積和の取得（Sum）：先頭から指定されたインデックスまでの累積和を計算します

区間の和に対するクエリ（Range Sum Query）を効率的に処理するデータ構造で、競技プログラミングでよく使われますが実務でも意外と便利です

この記事では、BIT（Fenwick Tree）を、Pythonで実装する方法について解説します。

BITを実装する

データの格納

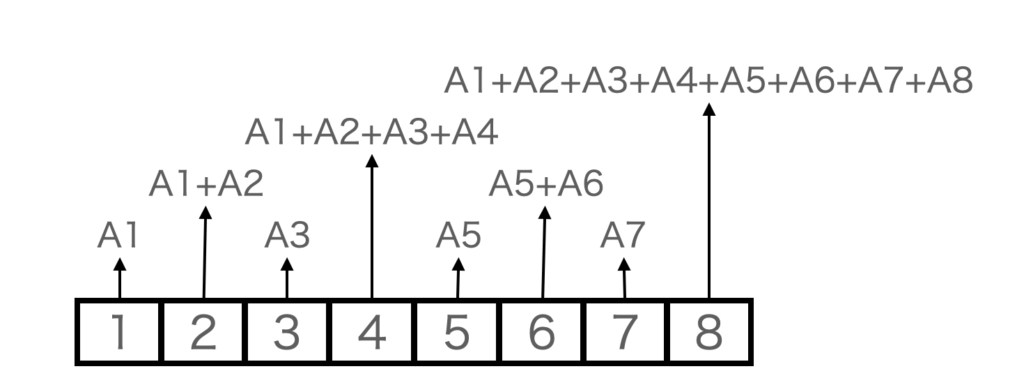
BITでは、要素数と同じN個の配列を用意し、それぞれ以下のような値を記録します（インデックスは1始まりです）。

例えば、要素数が８個で要素の値をA1, A2, A3 … , A8とした場合、各要素には以下のような値を記録します。

図からわかるように、要素１はA1を、要素２はA1+A2を、要素8は、A1~A8の和を記録しています。

BITでは、このように計算したデータを格納することで区間和を高速に計算することが可能としています。

先頭要素からの総和を算出

この配列を使って、例えば要素１〜７までの総和を計算する場合を考えます。

この場合、要素７、要素６、要素４の３つの値を加算すればA1~A7の総和になることがわかります。

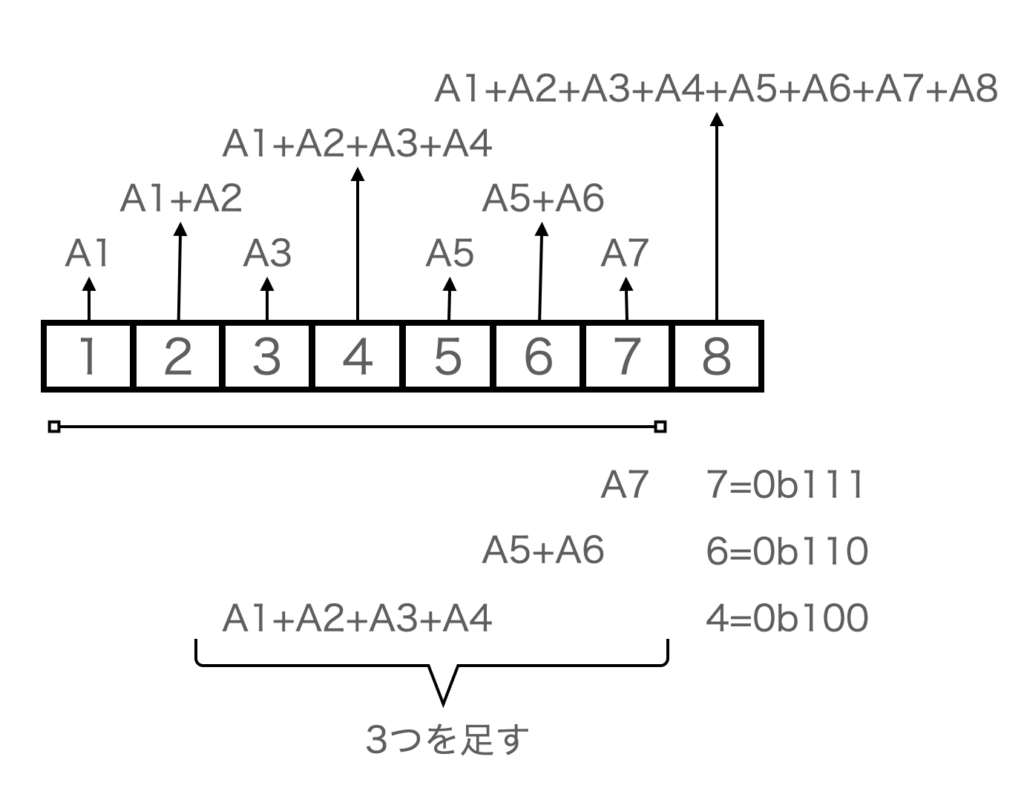
ここで、７、６、４という数字を２進数に変換して見ると0x111, 0x110, 0x100と、下位ビットが1の部分を0にしたものが並んでいることがわかります。

実は、このように要素番号を下位ビットから調べて1が立っている部分を0に変えた要素を合計すると先頭から要素番号までの総和になります。

例えば、要素番号１〜６までの総和は、6(0b110)→4(0b100)の和、１〜3までの和は3(0b11)→2(0b10)の和で計算することができます。

上図を見て確認してみてください。確かに、上記のような規則があることがわかります。

つまり、下位ビットから1を0にしていけば、加算する要素がわかることになります。

下位ビットが１の要素は”i&-i“で計算できる

実は、１が立っている一番下のビットは、i&-iという演算で計算することができます。

２の補数を理解していないと難しいですが、4bitの場合、6(0b0110)の符号を反転した-2は0b1001に1を足した0b1010になります。この２つのANDを取ると、0b0110&0b1010=0b0010となり、１が立っている最下位ビットが取り出せます。

最初に見た時は結構感動しました。

加算する要素は以下の計算で調べることができる

つまり、７→６→４という要素は、以下のようにi -= i&-iという簡単な式で計算できます。

この値が０になるまで繰り返せば、１〜要素までの加算ができます。

値の更新（加算）

次にある要素の値に加算する場合を考えます。

たとえば、要素５を更新する場合、A5が記録されている５、６、８の要素に値を加算すればOKです。

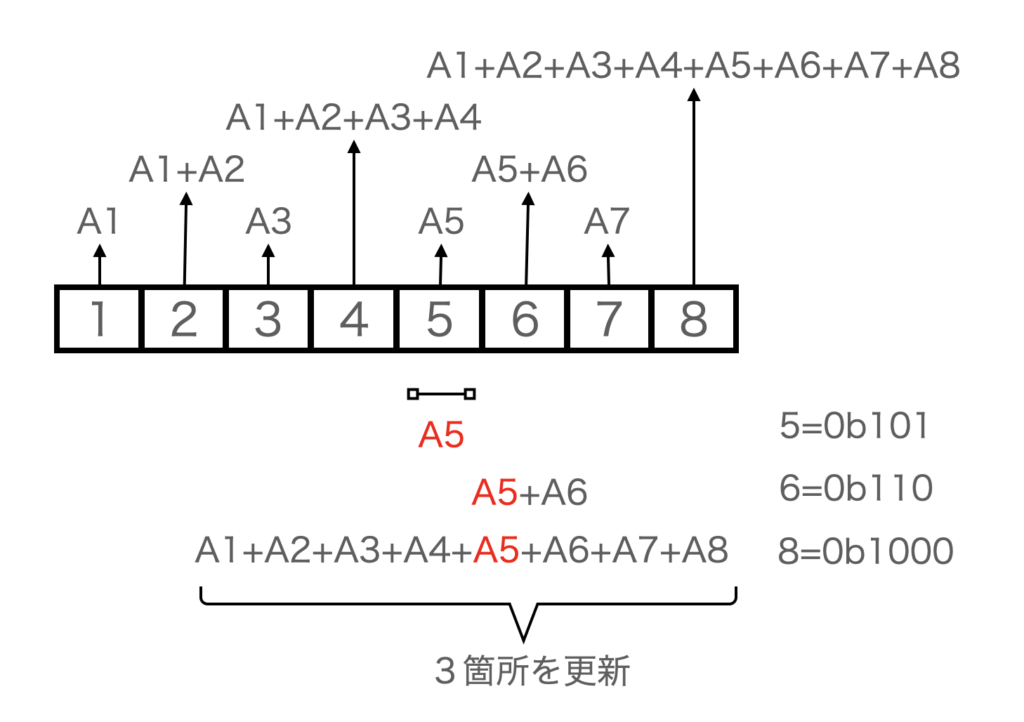
この計算も、以下のような計算で見つけることが可能です。

実装例（Python）

上記を踏まえてPythonで実装してみます。用意した関数は以下の通りです。

• __init__(n)
  n個の要素に初期化します
• add(i, x)
要素iにxを加算します
• sum(x)
区間[1, x]の累積和を返します
• range_sum(l, r)
区間[l, r]の累積和を返します
  range_sumは、要素rまでの合計から要素lまでの合計を引くことで計算できます

class BIT :
    def __init__(self, n) :
        self.size = n
        self.bit = [0] * (n + 1)

    def add(self, i, x) :
        while i <= self.size :
            self.bit[i] += x
            i += i & -i

    def sum(self, i) :
        s = 0
        while i > 0 :
            s += self.bit[i]
            i -= i & -i
        return s
    
    def range_sum(self, l, r) :
        return self.sum(r) - self.sum(l-1)

アルゴリズムは先ほど説明した通りです。なお、range_sumは、右端までのsumから左端（左端-1）までのsumを減算することで簡単に実装できます。

以下は、BITの利用例です。

bit = BIT(10)

for i in range(10) :
    bit.add(i+1, i+1)

print(bit.bit)

# val = 1,2,3,4,5,6,7,8,9,10
# sum = 1,3,6,10,15,21,28,36,45,55
for i in range(1, 11) :
    print(bit.sum(i))

print(bit.sum(4), bit.sum(2))
print(bit.range_sum(2, 4))

[0, 1, 3, 3, 10, 5, 11, 7, 36, 9, 19]
1
3
6
10
15
21
28
36
45
55 # 1-10 = 1+2+3+4+5+6+7+8+9+10=55
9 # [2,4] = 2+3+4

まとめ

Binary Indexed Tree（BIT）の実装方法について解説しました。なんとなく難しそうに見えますが実装はかなりシンプルです。区間和の計算と値の更新を高速に行うことができるので、いろいろなシーンで重宝するデータ構造です。特に、競プロでは頻繁に利用しますので、覚えておいて損はないです。

ある/Aru

IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)

XContact

専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中