深層学習の指標Perplexityを解説【初級 深層学習講座】
畳み込み層（CNN, Conv1D）の動きをわかりやすく解説 【初級 深層学習講座】
Aru
この記事では、画像のクラス分類や認識タスクで広く利用されている畳み込みネットワーク（CNN）の畳み込み層（Convolution Layer）について詳しく解説します。数式と図解を交えながら畳み込み層の仕組みを説明し、さらにPyTorchのコードを用いて実際の畳み込み層の動きを確認していきます。
Contents
畳み込み層（Convolution Layer）とは
簡単に言えば、畳み込み層は画像処理のフィルタ（デジタルフィルタ）処理に相当する処理行う層です。
一般的な画像処理では、画像の特徴をとらえるために、$3\times 3$, $5\times 5$, $7\times 7$といったサイズのフィルタを用意し、画像に対してフィルタ処理を行うことでエッジ抽出などの処理を行います(wikipediaのエッジ抽出の項目)。
例えば、ラプラシアンフィルタと呼ばれるフィルタは以下のような$3 \times 3$の係数を持ちます。
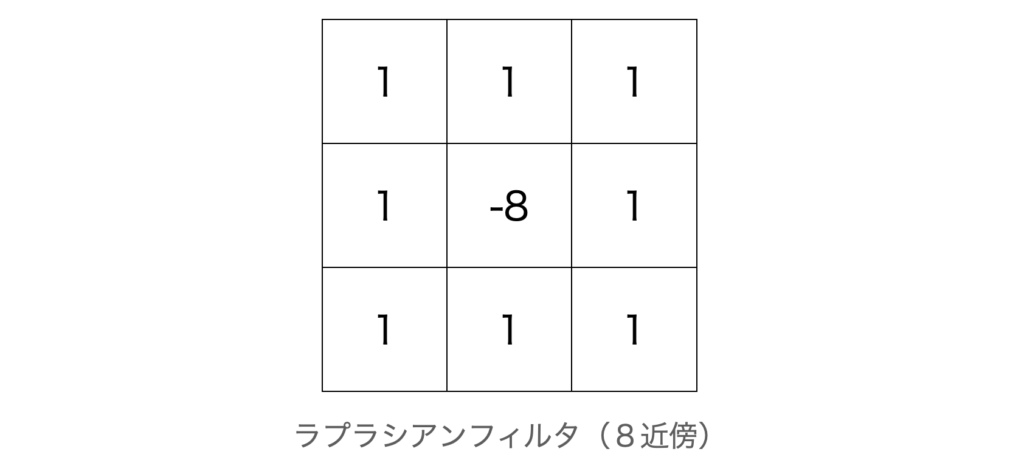
中央から周辺８近傍の値を引くこの計算は、以下のような数式の演算になります（中央を$v_c$, 周辺を$v_1$~$v_8$とした場合）。
$$
result = \sum_{i=1}^{8}{(v_i – v_c)}
$$
この数式を定性的に考えると、中央の画素と周辺の画素の差＝傾斜を計算していることになります。
画像では、この傾斜が小さい部分は平坦、大きい部分はエッジと考えることができます。このフィルタは傾斜が大きいほど大きな値になるため、このフィルタはエッジ抽出として機能するわけです。
これまでの画像処理では、このフィルタを抽出したい特徴に併せて設計し、例えばエッジなどの特徴を抽出していました。畳み込み層は、このフィルタの係数を学習によって自動で決めてしまおうというものです。
畳み込みネットワークは、複数のチャネルを持つことが多いですが、１つの１チャネルが１つのフィルタに対応します。複数のチャネルを持つことで複数の種類のフィルタ処理を一気に行っていることになります。
私は、もともとは画像処理が専門でした。フィルタ設計も行っていましたが、特徴を抽出するフィルタを32個（チャネル）とか128個（チャネル）手動で設計するのは困難です。学習により画像に合わせたフィルタを設計を作り、複数の特徴を画像から抽出するフィルタが自動的に設計できることがCNNの強みです。
まとめ
畳み込み層は、エッジ抽出のような画像のフィルタを行うもの
畳み込み層の動きを確認する
畳み込み層の動きを確認する手順
動きを確認するために、Pytorchを使って実際に出力を確認したいと思います。画像処理では、２次元の畳み込み（Conv2d）が使われますが、ここでは、１次元の畳み込み（Conv1d）を使って実験します。
Conv1Dを使う理由は、どちらも動きとしては同じであることと、手計算をやる場合に１次元の方が簡単だからです。
以下、Conv1dをつかって畳み込み層を見ていくことにします。
Conv1dのオブジェクトを生成する
PytorchのConv1dのリファレンスを見ると、以下のようなインタフェースになっています。
torch.nn.Conv1d( in_channels,
out_channels, kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros',
device=None,
dtype=None)
今回使うパラメータは、以下の３つです。
- in_channels 入力チャネル数
- out_channels 出力チャネル数
- kernel_size カーネルサイズ
kernel_sizeは、フィルタのサイズです。実際に、入力チャネル１、出力チャネル2、カーネルサイズ３で、Conv1dのオブジェクトを生成してみます。
import torch
from torch import nn
conv1d = nn.Conv1d(1,2,3)Conv1dのオブジェクトには、フィルタの係数（重み）とオフセット（バイアス）が格納されています。以下のコードで、重みとバイアスが確認できます。
print("weights", '-'*20)
print(conv1d.weight.shape)
print(conv1d.weight)
print("bias", '-'*20)
print(conv1d.bias.shape)
print(conv1d.bias)出力は以下のようになります
出力
weights --------------------
torch.Size([2, 1, 3])
Parameter containing:
tensor([[[ 0.2690, -0.3829, 0.5537]],
[[ 0.3526, -0.1392, 0.3159]]], requires_grad=True)
bias --------------------
torch.Size([2])
Parameter containing:
tensor([-0.0382, -0.4261], requires_grad=True)出力チャンネルを２にしたので、重みは2×3、バイアスは2個あることが確認できます。
このままだと面倒なので、重みを[1.0, 1.0, 1.0], [-1.0, 2.0, 1.0]、バイアスを[0.0, 0.0]に変更します。パラメータの変更は以下のコードで行うことができます。
conv1d.weight = nn.Parameter(torch.tensor([[[1.,1.,1.]],[[-1.,2.,-1.]]]))
conv1d.bias = nn.Parameter(torch.tensor([0., 0.]))
# 変更されているか確認
print("weights", '-'*20)
print(conv1d.weight.shape)
print(conv1d.weight)
print("bias", '-'*20)
print(conv1d.bias.shape)
print(conv1d.bias)出力
weights --------------------
torch.Size([2, 1, 3])
Parameter containing:
tensor([[[ 1., 1., 1.]],
[[-1., 2., -1.]]], requires_grad=True)
bias --------------------
torch.Size([1, 2])
Parameter containing:
tensor([0., 0.], requires_grad=True)バイアスが０なので、重みをフィルタとして考えた場合、以下のようなフィルタを２つ用意したことになります。
入力データを用意する
入力データを用意します。入力データの以下のような３次元データです。pytorchでは複数のデータを一度に渡せるように、バッチサイズが１次元目にくることに注意します。
（バッチサイズ、入力チャネル数、入力データ）
今回は、バッチサイズは１、入力チャネル数は１、入力データ長は１０でデータを作ってみます。
x = torch.tensor([[[float(i) for i in range (1, 11)]]])
print(x.shape)
print(x)作成したデータは、[1,2,3,4,5,6,7,8,9,10]というデータになります。
出力
torch.Size([1, 1, 10])
tensor([[[ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.]]])
Conv1dで畳み込みを行ってみる
入力データができたので、Conv1dで畳み込みを行ってみます。
y = conv1d(x)
print(y)出力
tensor([[[ 6., 9., 12., 15., 18., 21., 24., 27.],
[ 0., 0., 0., 0., 0., 0., 0., 0.]]],
grad_fn=<ConvolutionBackward0>)結果を見ていきます。重みを$w_0, w_1, w_2$、バイアスを$b$とすると、データに対する計算は以下になります。
$$
y[i] = w_0 \times x[i-1] + w_1 \times x[i] + w_2 \times x[i+1] + b
$$
また、入力は10個ですが、フィルタの長さが3なので、結果は8個となります。
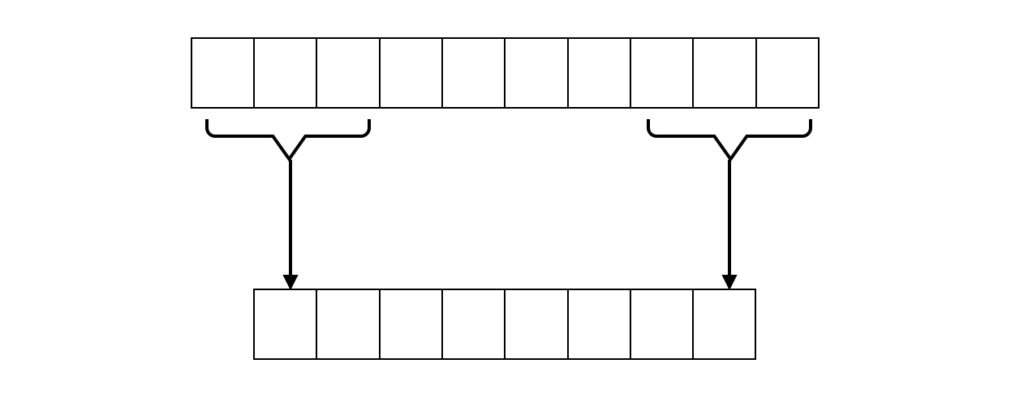
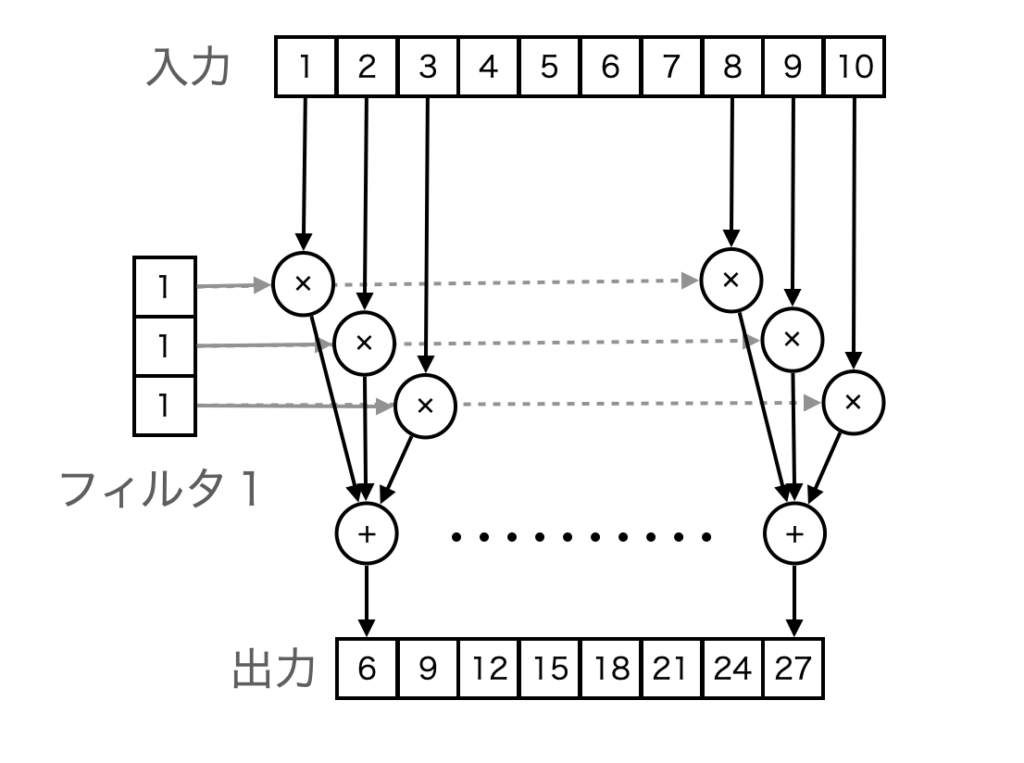
上の式に当てはめると、1つ目のフィルタはw=(1,1,1)でb=0となります。ですから、隣接する3つの値を加算した値がフィルタ結果となります（下図）。
実際に、[6., 9., 12., 15., 18., 21., 24., 27.]となっているのがわかります。
また、2つ目のフィルタはw=(-1,2,-1)で、b=0なので、計算すると全て０となり、こちらも出力結果と一致します。
まとめ
畳み込み層は、画像処理を行うネットワークでは基本となる層です。
この記事では、１次元の畳み込みについて実際に動かして動作を確認してみました。このように、わからない場合は、実際に動かして１つ１つのパーツの動きを確認してみると理解が進むかと思います。
ディープラーニングに関する記事一覧はこちら
ディープラーニング関連の記事一覧
ABOUT ME
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
