3重ループで最短経路を探索する方法（ワーシャルフロイド法）をPythonで実装する

Aru

ワーシャル・フロイド法は、比較的シンプルに実装できる最短経路探索アルゴリズムです。全頂点間の最短経路を効率的に計算でき、小規模なグラフに対して実用的な手法です。本記事では、ワーシャル・フロイド法のアルゴリズムと3重ループを用いたPythonによる実装方法を解説します。

Contents

ワーシャル・フロイド法
- ワーシャル・フロイド法
- アルゴリズム
実装例
- 実装するグラフ
- Pythonによる実装
まとめ

ワーシャル・フロイド法

ワーシャル・フロイド法は、グラフ理論の最短経路問題を解くためのアルゴリズムの１つです。このアルゴリズムを使うことで、グラフ上のすべての頂点間の最短経路を効率よく求めることが可能です。

このアルゴリズムの計算量は$O(n^3)$です。特定の頂点からの最短経路を求めるだけであれば、ダイクストラ法などをの方が計算量は小さいですが、実装は軽いです。

計算量は若干重めですが、100頂点くらいまでは高速に計算できるので競技プログラミングなどでも頻繁に利用されるアルゴリズムとなります。

アルゴリズム

基本的な考え方

ワーシャル・フロイド法の基本的な処理は、「２つの頂点間を移動する場合、他の点を経由して短い経路が見つかる可能性がある」という考え方に基づきます。これを実現するために、ワーシャルフロイドでは、３重ループを利用した処理を行います。

3重ループの役割

ワーシャル・フロイドは単純な３重ループで実装されることが多いです。

下記の例は、２次元配列d[n][n]に各経路の距離が格納されている場合のワーシャルフロイドのループになります。なお、配列dは以下のように初期化されているとします。

頂点をxとしたとき、d[x][x]（自分自身への距離）は0とする
2つの頂点x, yが距離Lで接続されている場合、d[x][y]=Lに初期化
それ以外は無限大（♾️、非常に大きな値）で初期化

for k in range(n):
  for i in range(n):
    for j in range(n):
      if d[i][j] > d[i][k] + d[k][j] : 
         d[i][j] = d[i][k] + d[k][j]

それぞれのループは、以下のような意味になります。

外側のループ: 経由する頂点kを1つずつ選択します。この頂点を経由することで、他の頂点間の経路が短縮できるかを確認します。
2番目のループ: 始点iとなる頂点を選択します。
3番目のループ: 終点jとなる頂点を選択します。

経路の更新部分では、以下の判定が行われますが、これは頂点iから頂点jへ頂点kを経由した方が近ければ更新するという処理になります。

      if d[i][j] > d[i][k] + d[k][j] : 
         d[i][j] = d[i][k] + d[k][j]

直接接続されていない点は、無限大（♾️）で初期化されているので、ある頂点ｋを経由して頂点iからjへいける場合は、その距離で更新される形になります。また、より短い経路があれば、それで更新されます。

i, j, kのループの順番を間違えないように注意してください。kのループが一番外側です。これを間違うとうまく最短経路を計算できません。

例

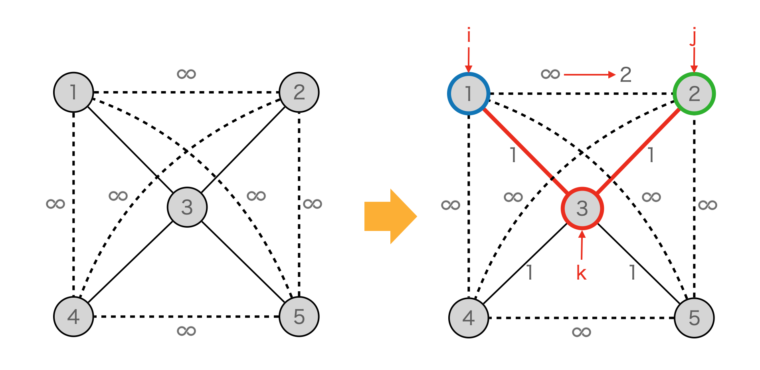
例えば、下図（左）のようなグラフがあるとします。このときi=1, j=2, k=3として考えると、直接接続されていない1から2の経路は、1→3→2の経路のコストの2に更新されます。このように、頂点kを経由するコストが小さい場合はそれで更新することで最短経路を求めていきます（下図（右））。

実装例

実装するグラフ

ここでは、以下のグラフの最短経路を探索してみます。

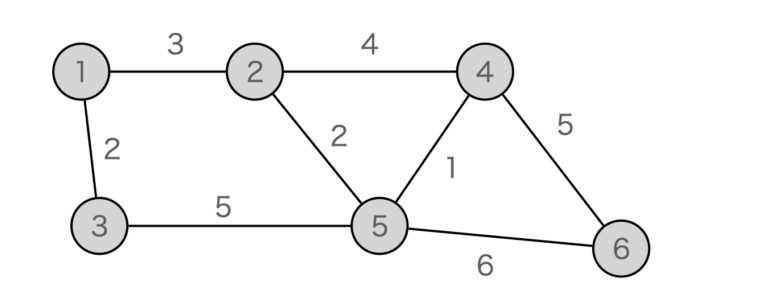
頂点1は、頂点2,3とコスト3,2で接続されています。これを（from, to, cost）の形式のタプルで表現すると以下のようになります。

g = (
    (1,2,3),(1,3,2),(2,4,4),(2,5,2),(3,5,5),(4,5,1),(4,6,5),(5,6,6)
)

ここでは、gを入力してワーシャル・フロイド法による最短距離計算をPythonで行ってみます。

Pythonによる実装

以下、ワーシャル・フロイド法による解法のプログラム例です。

inf = 10**5
n = 6
d = [[inf for _ in range(n)] for _ in range(n)]

g = (
    (1,2,3),(1,3,2),(2,4,4),(2,5,2),(3,5,5),(4,5,1),(4,6,5),(5,6,6)
)

for i in range(n):
    d[i][i] = 0

for f,t,l in g :
    f -= 1
    t -= 1
    d[f][t] = l
    d[t][f] = l

print("d = ")
for i in range(n):
    for j in range(n):
        print(f"{d[i][j]:6d} ", end=" ")
    print()


for k in range(n):
    for i in range(n):
        for j in range(n):
            if d[i][j] > d[i][k] + d[k][j] : 
                d[i][j] = d[i][k] + d[k][j]


print("-"*50)
print("result = ")
for i in range(n):
    for j in range(n):
        print(f"{d[i][j]:6d} ", end=" ")
    print()

処理結果は以下のようになります。

上が初期の距離配列dの値、result=以降が各点からの最短距離です。

d = 
     0       3       2  100000  100000  100000  
     3       0  100000       4       2  100000  
     2  100000       0  100000       5  100000  
100000       4  100000       0       1       5  
100000       2       5       1       0       6  
100000  100000  100000       5       6       0  
--------------------------------------------------
result = 
     0       3       2       6       5      11  
     3       0       5       3       2       8  
     2       5       0       6       5      11  
     6       3       6       0       1       5  
     5       2       5       1       0       6  
    11       8      11       5       6       0

以下、順番に解説します。

配列dを初期化

まず、距離の配列d[n][n]を初期化します。最初に全体を最大距離（♾️、ここでは100000）に設定し、d[x][x]=0に初期化します。

その後、グラフの情報gを基にして直接接続されている辺を張っていきます。

最後に初期の配列dの状態を表示して終了です。

inf = 10**5
n = 6
d = [[inf for _ in range(n)] for _ in range(n)]

g = (
    (1,2,3),(1,3,2),(2,4,4),(2,5,2),(3,5,5),(4,5,1),(4,6,5),(5,6,6)
)

for i in range(n):
    d[i][i] = 0

for f,t,l in g :
    f -= 1
    t -= 1
    d[f][t] = l
    d[t][f] = l

print("d = ")
for i in range(n):
    for j in range(n):
        print(f"{d[i][j]:6d} ", end=" ")
    print()

ワーシャル・フロイド法

距離配列dが初期化できたら、ワーシャル・フロイド法は単純な３重ループとして実装できます。ここは、先に説明した通りです。

処理後のdは、各点からの最短距離の配列になります。

for k in range(n):
    for i in range(n):
        for j in range(n):
            if d[i][j] > d[i][k] + d[k][j] : 
                d[i][j] = d[i][k] + d[k][j]


print("-"*50)
print("result = ")
for i in range(n):
    for j in range(n):
        print(f"{d[i][j]:6d} ", end=" ")
    print()