2進数の1が立っているビットを高速にカウントする方法|Python

この記事では、2進数表記で「1」が立っているビットの数を、高速にカウントするためのアルゴリズムについて詳しく解説します。ビットカウント処理は、データ圧縮、エラー訂正、データ解析などの分野で利用され、処理パフォーマンスに影響を与える要素となっています。効率的なビットカウント技術を習得し、ビット演算処理の面白さと奥深さを体験してみましょう。
はじめに
整数値の2進数表記で「1」の数を数える(立っているビットをカウント)する関数は、色々なプログラミング言語に備わっています。
例えばGo言語ならmath/bitsパッケージにbits.OnesCount()関数が用意されていますし、Pythonなら整数型にbit_count()メソッドが用意されています。
ビットカウントを行う関数では、どのような処理が行われているのでしょうか?
この記事では、1が立っているビットの数をカウントするアルゴリズムをいくつか紹介し、高速にカウントするためにどのような方法があるのかを紹介したいと思います。

ここでは、簡単のために16bitの値の場合について限定して解説します。32bitなどでも原理は同じなので自身で考えてみてください。
以下、Pythonを使って、ステップを踏みながら高速化していきたいと思います。
愚直解:ループでカウントする方法
一番最初に思いつくのは、「各ビットに1が立っているかどうかをチェックし、ビットが立っていればカウンタを+1する方法」ではないでしょうか。
これを愚直に実装したコードが以下のbit_coun関数になります。
import random
def bit_count(n) :
cnt = 0
for i in range(16):
if n%2 == 1 :
cnt+=1
n = n >> 1
return cnt
for i in range(10) :
n = random.randint(0, 1<<16)
ret = bit_count(n)
print(f"{n:5d} {format(n, '016b')} {ret:2d}")
## 結果
# 10990 0010101011101110 9
# 6376 0001100011101000 6
# 16317 0011111110111101 12
# 461 0000000111001101 6
# 32862 1000000001011110 6
# 33942 1000010010010110 6
# 20334 0100111101101110 10
# 12231 0010111111000111 10
# 5558 0001010110110110 8
# 45558 1011000111110110 10bit_count関数では、最下位ビットに1が立っているかどうかをn%2==1という式でチェックし、1が立っていればcnt+=1とカウンタを更新しています。
n=n>>1と、1ビットづつ右シフトしながらこの処理を16回繰り返します。
これで、全てのビットに1が立っているかどうかをチェックでき、結果がcntに格納されます。
プログラムの実行結果を見ても、ビットが1の数を正しくカウントできていることがわかります。
このプログラムは、bit数分ループを繰り返すします。16bitなら16回、32bitなら32回繰り返すことになります。一度だけなら、それほどの処理ではないですが、数万回、数十万回繰り返す場合は結構なインパクトとなります。
高速にカウントする方法
愚直解では、「1ビットずつチェックし、カウント」していました。高速にするには、どうしたら良いでしょうか?
直感的は、「まとめて1をカウントできればいいんじゃない?」とおもいつくかもしれません。
実は、「複数ビットをまとめてカウントする」という考え方は正解です。では、どうやればまとめてカウントできるでしょうか?
その方法が、アルゴリズムのテクニカルな部分になります。
アルゴリズム
アルゴリズムの概要は以下になります。
アルゴリズムの概要
入力された値をNとします。
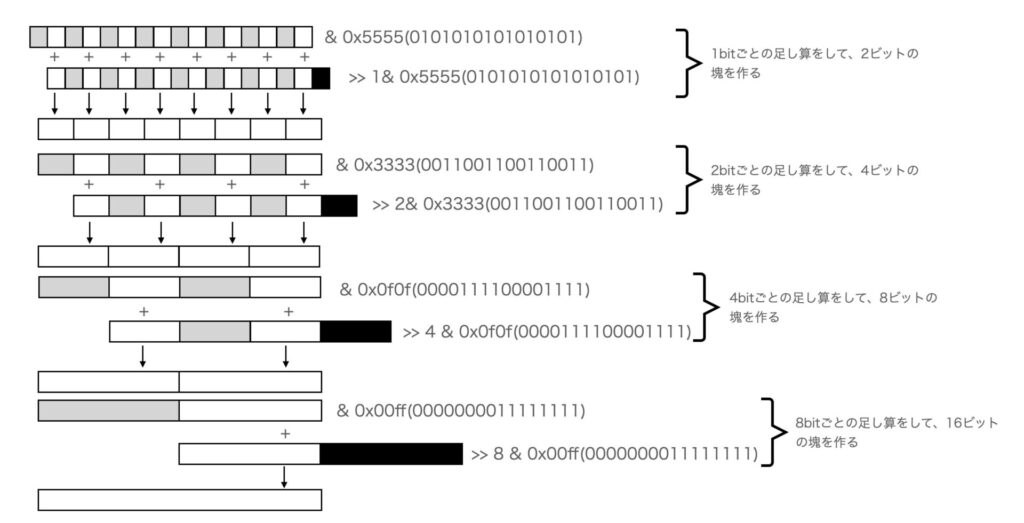
まず、Nを0b01010101_01010101(0x5555)でマスクします。すると2ビット単位で見ると、下位1ビットだけを取り出した値が作られます。

ここでは、2進数表記を”0bxxxxxxxx_xxxxxxxx“と表記しています。_を8bit区切りでつけることで数をわかりやすくしています。
次にNを1ビット右シフトして同じように0b01010101_01010101でマスクします。すると、1ビット右にシフトしてからマスクしたので、こちらは、2ビット単位で考えた場合、上位1ビットだけを取り出した値が作られたことになります。
この状態で、0b0x0x0x0x_0x0x0x0x(xは0または1)という形の2つの値(2ビット単位で上位と下位ビットを取り出したもの)が作られました。
これを足すと、1bitの足し算が同時に8個行うことができます。ポイントは、各演算は0+0=0, 1+0=1, 0+1=1, 1+1=2(0b10)のどれかの値しか取らないので、結果も2ビットに収まることです。
次に、マスク幅を4bitに変えて(0b00110011_00110011=0x3333)、同様のマスクとシフト演算、足し算を行います。これで4つの値の足し算ができます。
さらに幅を8bitに変えて(0b00001111_00001111=0x0f0fのマスク)、同様のマスクとシフト演算、足し算を行います。これで2つの値の足し算ができます。
最後に16bitで(0b00000000_11111111=0x00ffのマスク)、同様のマスクとシフト演算、足し算を行います。これで全てのビットの加算が完了します。
この結果は、1が立っているビットの数と一致します。
具体例を使って解説
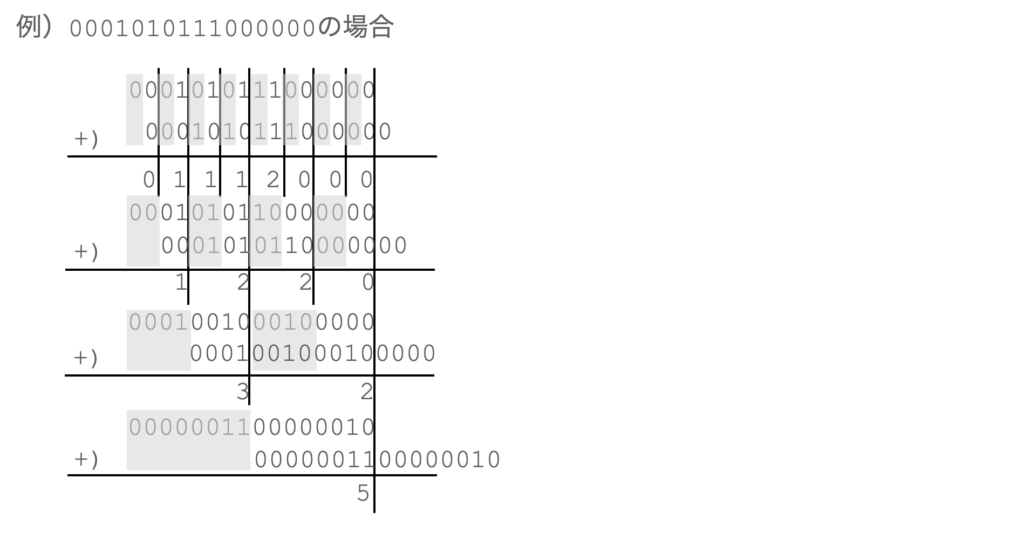
わかりにくいの具体例で解説します。下図は、0001010111000000の1のビット数を数える例です。
まず、2桁に区切って足し算を行います。このとき上位1bitはマスクします(0にします)。
図では、マスクされた部分をグレーにしています(また、片方は1ビット右シフトしています)
次に、4bitごとで演算します。4bitの演算では、0b0011=0x3という値で各4bitをマスクします。ここでは、片方を2ビットシフトします。
次は8bitで演算します。8bitの演算では、0b00001111=0x0fという値で各8bitをマスクします。ここでは、片方を4ビットシフトします。
これを繰り返すと1が立っている数が、8個同時、4個同時、2個同時…と足し込まれていき、最終的に全体の1が立っている数が計算できます。
実際に、結果は5となり、このアルゴリズムが正しいことがわかります。
具体的なプログラムコード
上記のアルゴリズムをプログラムしたのがbit_count2()です。
プログラムを見たらわかるように、ループは存在せず、4回のシフト、8回のand、4回の足し算だけで計算が終了します。
ループを使ったプログラムでは、(条件判定1回、加算1回、シフト1回)×16回行っているので、演算量が少なくなっていることがわかります。
def bit_count2(n) :
n = (n & 0x5555) + (n >> 1 & 0x5555)
n = (n & 0x3333) + (n >> 2 & 0x3333)
n = (n & 0x0f0f) + (n >> 4 & 0x0f0f)
n = (n & 0x00ff) + (n >> 8 & 0x00ff)
return n
このやり方は、bit数が多いほど効果が高いです。例えば32bit長、64bit長でのビットカウントはさらに効果的になります。
結果確認
正しく計算できているか、bit_count()とbit_count2()の結果を比較してみます。
import random
def bit_count(n) :
cnt = 0
for i in range(16):
if n%2 == 1 :
cnt+=1
n = n >> 1
return cnt
def bit_count2(n) :
n = (n & 0x5555) + (n >> 1 & 0x5555)
n = (n & 0x3333) + (n >> 2 & 0x3333)
n = (n & 0x0f0f) + (n >> 4 & 0x0f0f)
n = (n & 0x00ff) + (n >> 8 & 0x00ff)
return n
for i in range(10) :
n = random.randint(0, 1<<16)
ret = bit_count(n)
print(f"{n:5d} {format(n, '016b')} {ret:2d}")
for i in range(10) :
n = random.randint(0, 1<<16)
ret1 = bit_count(n)
ret2 = bit_count(n)
print(f"{n:5d} {format(n, '016b')} {ret1:2d} {ret2:2d}")
## 結果
# 65357 1111111101001101 12 12
# 38119 1001010011100111 9 9
# 28729 0111000000111001 7 7
# 13614 0011010100101110 8 8
# 9112 0010001110011000 6 6
# 43197 1010100010111101 9 9
# 31144 0111100110101000 8 8
# 24819 0110000011110011 8 8
# 43637 1010101001110101 9 9
# 58173 1110001100111101 10 10実際に実行してみると両者は同じ値となり、高速化したアルゴリズムで正しく計算できていることが実行結果からも確認できました。
処理時間計測
では、どれくらい高速化できたかをチェックしてみます。下記のプログラムでは、処理を1000万回繰り返して測定しています。
import time
def bit_count(n) :
cnt = 0
for i in range(16):
if n%2 == 1 :
cnt+=1
n = n >> 1
return cnt
def bit_count2(n) :
n = (n & 0x5555) + (n >> 1 & 0x5555)
n = (n & 0x3333) + (n >> 2 & 0x3333)
n = (n & 0x0f0f) + (n >> 4 & 0x0f0f)
n = (n & 0x00ff) + (n >> 8 & 0x00ff)
return n
start = time.time()
n = 10_000_000
for i in range(n) :
bit_count(i)
end = time.time()
print(f"{(end - start)} sec")
# 7.029723882675171 sec
start = time.time()
for i in range(n) :
bit_count2(i)
end = time.time()
print(f"{(end - start)} sec")
# 1.8477487564086914 sec結果を見るとループ版(bit_count)では7.03秒、高速化版(bit_count2)では1.85秒と3.8倍高速に処理できています。
ビットをカウントする処理を繰り返すようなプログラムの場合、この処理時間の差は結構効いてきます。
ビット演算には、いろいろ面白い性質があります
その①:x&-xをすると1が立っている最下位ビットだけ残るという性質があります。これを使った応用例が以下の記事あります。

その②:XORは1ビットの足し算として使えます。これを使った例が以下の記事になります。

まとめ
2進数で見た時に1が立っている数を数える処理を、高速化するアルゴリズムについて解説しました。このアルゴリズムは結構一般的に利用されているものです。ビット演算には面白いテクニックが多数あります。興味がでた方はいろいろ調べてみてはいかがでしょうか。