深層距離学習と近似最近傍探索による特徴量マッチング|Pytorch Metric Learning+Faiss

本記事では、Pytorch Metric Learningを用いて、顔認証の基盤技術である深層距離学習(Deep Metric Learning)をMNISTデータセットで実践します。さらに、Faissを用いた近似最近傍探索による特徴量の高速マッチングを行い、これらの技術の組み合わせ方を詳しく紹介します。この記事を通じて、顔認証に必要な技術の組み合わせ方を学ぶことができます。
FAISSをテキスト検索に使う方法については以下の記事を参考にしてください

はじめに
顔認証で利用されている深層距離学習のコードに興味があったので、実際に自分で実装してみることにしました。実際に顔認証を行うことも考えましたが、学習用のデータセット収集に苦労しそうだったので、MNISTの手書き数字のデータセットを使ってテスト実装することにしました。
MNISTデータセットを使用しても、深層距離学習の基本的な考え方は顔認証と同じです。
実装には、Pytorch Metric Learningという距離学習専用のライブラリを利用しています。このライブラリを使うことで、距離学習の実装が大幅に楽になります。
顔認証では、深層距離学習で学習したモデルが出力する特徴量(特徴ベクトル)のマッチング処理が必要です。今回は、特徴量間の距離計算にFaissを使用します。Faissを用いることで、近傍探索を高速に行うことができ、数万件の顔画像とのマッチングも迅速に実行可能となります。
Pytorch Metric LearningとFaissを組み合わせることで、特徴ベクトルの抽出と高速なマッチングが実現できます。この2つの技術の組み合わせを理解することで、顔認証の基本を理解することができます。
Google Colabで動作するコードはこちらです
実際に顔認証を行う場合以下の記事も参考にしてください。

PyTorch Metric Learningとは
PyTorch Metric Learningとは、深層距離学習に必要な機能をモジュールとして提供するPyTorch向けのライブラリです。
これを利用すれば、既存のコードをわずかに修正するだけで、深層距離学習を行うことができます。
FAISSとは
Faiss(Facebook AI Similarity Search)は、ベクトル検索するためのMetaが作成したライブラリです。これを使うことで、ベクトルの近似最近傍探索(類似検索)を高速で行うことが可能です。
今回は、このライブラリを、特徴量ベクトルのマッチングに利用します。
ライブラリのインストール
この記事では、UMAPとFAISS、Pytorch Metric Learningを使いますので、これをインストールする必要があります。
Google ColabやJupyter notebookの場合は以下のコードをセルで実行することでインストールできます。
ローカル環境の場合は、!を外してコマンドラインでpipコマンドを実行してください。
!pip install umap-learn
!pip install pytorch-metric-learning
!pip install faiss-cpuベースとするMNISTデータセットの学習コード
ベースとするコードはMNISTの手書き数字をクラス分類するコードです。
このコードについては、以下の記事で詳しく説明していますので、そちらを確認してください。

修正前の学習コードは以下になります。これを深層距離学習に対応させていきます。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import matplotlib.pyplot as plt
import numpy as np
from tqdm.notebook import tqdm
from sklearn.metrics import accuracy_score
train_dataset = torchvision.datasets.MNIST(root="data",
train=True,
transform=torchvision.transforms.ToTensor(),
download=True)
valid_dataset = torchvision.datasets.MNIST(root="data",
train=False,
transform=torchvision.transforms.ToTensor(),
download=True)
batch_size = 64
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
valid_loader = torch.utils.data.DataLoader(valid_dataset, batch_size=batch_size, shuffle=False)
class MyModel(nn.Module):
def __init__(self, input_size):
super(MyModel, self).__init__()
self.size = input_size*input_size
self.fc1 = nn.Linear(self.size, 1024)
self.fc2 = nn.Linear(1024, 256)
self.fc3 = nn.Linear(256, 10)
def forward(self, x):
x = x.view(-1, self.size)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
device = "cuda" if torch.cuda.is_available() else "cpu"
model = MyModel(28).to(device)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
def do_train(model, device, loader, criterion, optimizer):
model.train()
tot_loss = 0.0
tot_score = 0.0
for images, labels in tqdm(loader, desc="train"):
images, labels = images.to(device), labels.to(device)
optimizer.zero_grad()
outputs = model(images)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
tot_loss += loss.detach().item()
tot_score += accuracy_score(labels.cpu(), outputs.argmax(dim=1).cpu())
tot_loss /= len(loader)
tot_score /= len(loader)
return tot_loss, tot_score
def do_valid(model, device, loader, criterion):
model.eval()
tot_loss = 0.0
tot_score = 0.0
with torch.no_grad():
for images, labels in tqdm(loader, desc="valid"):
images, labels = images.to(device), labels.to(device)
outputs = model(images)
loss = criterion(outputs, labels)
tot_loss += loss.detach().item()
tot_score += accuracy_score(labels.cpu(), outputs.argmax(dim=1).cpu())
tot_loss /= len(loader)
tot_score /= len(loader)
return tot_loss, tot_score
num_epochs = 10
for epoch in range(num_epochs):
print(f'[EPOCH {epoch+1}]')
train_loss, train_acc = do_train(model, device, train_loader, criterion, optimizer)
valid_loss, valid_acc = do_valid(model, device, valid_loader, criterion)
print(f"--> train loss {train_loss}, train accuracy {train_acc}, valid loss {valid_loss} valid accuracy {valid_acc}")深層距離学習を行う
以下、深層距離学習を行うコードになります。ここから下のコードが、実装するコードです。以下で説明するコードを繋げることで深層距離学習のコードが完成しますので、自身で試す場合はここのコードからコピペしてください。
クラス分類と共通の部分
以下の部分はクラス分類と共通です。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import matplotlib.pyplot as plt
import numpy as np
from tqdm.notebook import tqdm
from sklearn.metrics import accuracy_score
train_dataset = torchvision.datasets.MNIST(root="data",
train=True,
transform=torchvision.transforms.ToTensor(),
download=True)
valid_dataset = torchvision.datasets.MNIST(root="data",
train=False,
transform=torchvision.transforms.ToTensor(),
download=True)
batch_size = 64
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
valid_loader = torch.utils.data.DataLoader(valid_dataset, batch_size=batch_size, shuffle=False)損失関数をPytorch Metric Learningからインポート
深層距離学習を行うために、損失関数をPytorch Metric Learningのものと入れ替えます。これを行うために、ライブラリからlossesをインポートします。
from pytorch_metric_learning import lossesモデルの定義を変更
クラス分類からモデルの定義を変更します。具体的には、クラス分類のための最終段のnn.Linearを削除します。
これで、モデルの準備は完了です。
class MyModel(nn.Module):
def __init__(self, input_size):
super(MyModel, self).__init__()
self.size = input_size*input_size
self.fc1 = nn.Linear(self.size, 1024)
self.fc2 = nn.Linear(1024, 256)
def forward(self, x):
x = x.view(-1, self.size)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return x
device = "cuda" if torch.cuda.is_available() else "cpu"
model = MyModel(28).to(device)
model損失関数と最適化手法を設定
損失関数と最適化手法を設定します
今回は、損失関数としてArcFaceLossを利用します。ArcFaceLossの引数は、クラス分類の数、埋め込み層の数(モデルの出力数)とscaleとmarginです。scaleはデフォルトの64を、margineは少し大きめの32を設定しました。
なお、オプティマイザー側も変更が必要です。
オプティマイザーに、損失関数内のパラメータ(metric.parameters())も加える必要があります。
metric = losses.ArcFaceLoss(num_classes=10, embedding_size=256, scale=64, margin=32).to(device)
optimizer = torch.optim.Adam(
[{'params': model.parameters()}, {'params': metric.parameters()}],
lr=0.001)学習用・評価用関数の修正
学習用と評価用の関数を修正します。
具体的にはaccuracyの出力をカットしているだけです。モデルの出力がクラス分類では無くなったので、評価できなくなったので削除しています。
それ以外は、クラス分類の関数と同じです。
def do_train(model, device, loader, criterion, optimizer):
model.train()
tot_loss = 0.0
for images, labels in tqdm(loader, desc="train"):
images, labels = images.to(device), labels.to(device)
optimizer.zero_grad()
outputs = model(images)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
tot_loss += loss.detach().item()
tot_loss /= len(loader)
return tot_loss
def do_valid(model, device, loader, criterion):
model.eval()
tot_loss = 0.0
with torch.no_grad():
for images, labels in tqdm(loader, desc="valid"):
images, labels = images.to(device), labels.to(device)
outputs = model(images)
loss = criterion(outputs, labels)
tot_loss += loss.detach().item()
tot_loss /= len(loader)
return tot_loss学習ループ
学習ループは変更ありません。
num_epochs = 10
for epoch in range(num_epochs):
print(f'[EPOCH {epoch+1}]')
train_loss = do_train(model, device, train_loader, metric, optimizer)
valid_loss = do_valid(model, device, valid_loader, metric)
print(f"--> train loss {train_loss}, valid loss {valid_loss}")実行結果を見ると、ロスが順調に減っている(学習できている)ことが分かります。ただ、marginを大きくしたためか、ロスがあまり減ってないです。

UMAPで確認
256次元の特徴量を2次元に次元圧縮して、UMAPで確認してみます。
model.eval()
features = None
classes = None
for images, labels in tqdm(valid_loader):
with torch.no_grad():
images = images.to(device)
outputs = model(images)
# print(outputs.shape)
if classes is None:
classes = labels.cpu()
else:
classes = torch.cat((classes, labels.cpu()))
if features is None:
features = outputs.cpu()
else:
features = torch.cat((features, outputs.cpu()))
import umap
umap = umap.UMAP(n_components=2, random_state=42)
X_umap = umap.fit_transform(features)
plt.scatter(X_umap[:, 0], X_umap[:, 1], c=classes)
plt.show()色分けは数字(ラベル)で行っています。これを見ると、それぞれの数字がうまく分離できていることが分かります。
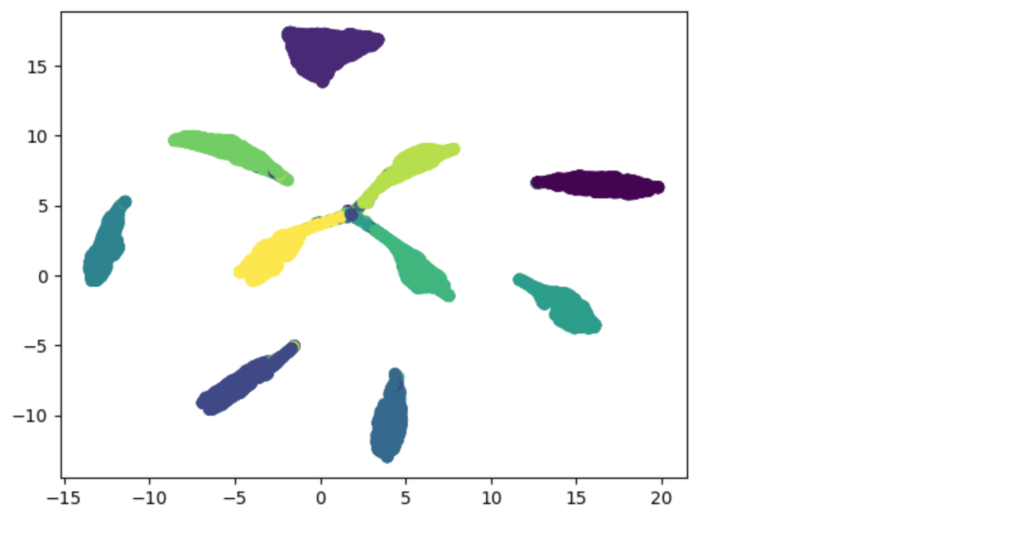
下図は、クラス分類のモデルの特徴量マップですが、これと比較すると同心円上に配置されているように見えます。ArcFaceはコサイン距離を使っているので同心円状に特徴量マップが変化するのは正しい動きと考えることができます。
(参考)クラス分類の場合のUMAPの結果
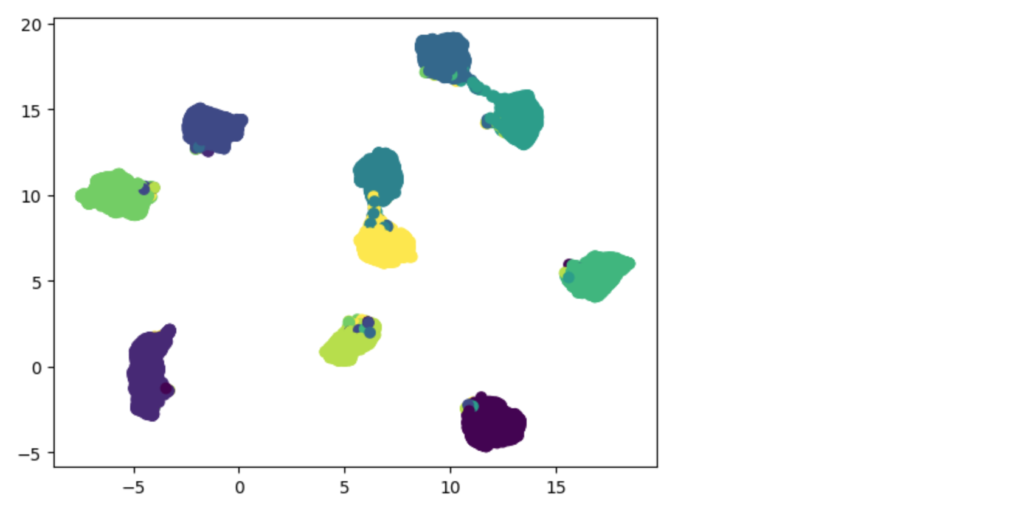
距離計算をやってみる
実際にベクトル間の距離計算(コサイン距離)を行ってみます。コードは以下になります。
from pytorch_metric_learning.distances import CosineSimilarity
# 最初のバッチについて特徴量を作成
images, labels = valid_loader.__iter__().__next__()
model.eval()
with torch.no_grad():
images = images.to(device)
features = model(images)
# 距離を計算
ret = CosineSimilarity()(features, features).cpu()
# 最初の文字とのコサイン距離が近いものを抽出する(閾値0.9)
print(f"label = {labels[0]}")
for i in range(64):
if ret[0][i] > 0.9 :
print("-"*40, end="")
print(f"score = {float(ret[0][i]):.3f} label = {int(labels[i])}")結果retは全てのペアに対する距離(64×64個)ですが、ここでは、1つめの候補との距離だけ出力しています。1つめの数字は7です。
自身との距離は1となります。似た文字との距離は1に近くなり、遠くなるほど0に近くなります。
結果を見ると、手書き文字のうち数字7との距離だけ近いと判定され、正しく距離学習が行われていることが確認できます。
実行結果
label = 7
----------------------------------------score = 1.000 label = 7
score = 0.018 label = 2
score = 0.016 label = 1
score = 0.000 label = 0
score = 0.002 label = 4
score = 0.019 label = 1
score = 0.003 label = 4
score = 0.000 label = 9
score = 0.000 label = 5
score = 0.004 label = 9
score = 0.013 label = 0
score = 0.058 label = 6
score = 0.000 label = 9
score = 0.022 label = 0
score = 0.061 label = 1
score = 0.010 label = 5
score = 0.000 label = 9
----------------------------------------score = 0.994 label = 7
score = 0.000 label = 3
score = 0.001 label = 4
score = 0.002 label = 9
score = 0.042 label = 6
score = 0.058 label = 6
score = 0.010 label = 5
score = 0.001 label = 4
score = 0.003 label = 0
----------------------------------------score = 0.963 label = 7
score = 0.002 label = 4
score = 0.006 label = 0
score = 0.064 label = 1
score = 0.002 label = 3
score = 0.073 label = 1
score = 0.002 label = 3
score = 0.002 label = 4
----------------------------------------score = 0.981 label = 7
score = 0.027 label = 2
----------------------------------------score = 0.972 label = 7
score = 0.068 label = 1
score = 0.004 label = 2
score = 0.049 label = 1
score = 0.066 label = 1
----------------------------------------score = 0.993 label = 7
score = 0.002 label = 4
score = 0.003 label = 2
score = 0.001 label = 3
score = 0.007 label = 5
score = 0.039 label = 1
score = 0.026 label = 2
score = 0.002 label = 4
score = 0.003 label = 4
score = 0.042 label = 6
score = 0.002 label = 3
score = 0.009 label = 5
score = 0.003 label = 5
score = 0.024 label = 6
score = 0.009 label = 0
score = 0.002 label = 4
score = 0.022 label = 1
score = 0.000 label = 9
score = 0.058 label = 5
----------------------------------------score = 0.971 label = 7
score = 0.011 label = 8
score = 0.000 label = 9
score = 0.007 label = 3FAISSによる近傍探索
深層距離学習が完了したので、FAISSを使って特徴ベクトルをデータベース化し、近傍検索を行ってみます。
ここでは、学習に利用したデータ6万件の特徴ベクトルをデータベースに登録し、検証データの特徴ベクトルを使って検索を行ってみます。

データベースには6万件のデータが登録されていて、それを近傍検索することになります
ライブラリのインポート
コードの実行に必要なライブラリをインポートします。
import faiss
import randomFAISSのインデックスを定義
インデックスを定義します。
今回は、特徴ベクトルのコサイン距離を距離として使いたいので、faiss.IndexFlatIP, faiss.METRIC_INNER_PRODUCTを設定しています。

特徴ベクトルが1に正規化されていれば、内積とコサイン距離は一致します。今回の特徴ベクトルは正規化されていないので正規化する必要がある点には注意します。
なお、faiss.IndexIVFFlatをコメントアウトしていますが、今回の場合はこちらを使っても良いです。登録件数が大量にある場合は、faiss.IndexIVFPQは量子化されるためメモリが節約できます(ただし、精度は落ちるそうです)。
dim = 256
nlist = 10
m = 32
nbits = 8
quantizer = faiss.IndexFlatIP(dim)
# index = faiss.IndexIVFFlat(quantizer, dim, nlist, faiss.METRIC_INNER_PRODUCT)
index = faiss.IndexIVFPQ(quantizer, dim, nlist, m, nbits, faiss.METRIC_INNER_PRODUCT)引数は以下の通りです
- dim=256:ベクトルの次元数の指定
- nlist=10:クラスター数の指定。FAISS(IVF)では全体のデータセットをいくつかのクラスターに分割します。nlistで、そのクラスター数を指定します
- m, nbits:ベクトル量子化のためのパラメータです。GPUの場合はnbits=8固定だそうです。mは、量子化器の数(?)です。
訓練データ(6万件)の特徴量を計算
6万件の特徴量とクラスのペアを計算し、featuresとclassesに格納します
output = (outputs....の行は、出力されたベクトルのL2正規化を行なっている部分です。
FAISSでは、cos距離がサポートされていないので、ベクトルを正規化しています。
正規化することでベクトルの内積がコサイン距離になります。
具体的には、以下の計算を行っています。
$$
output = \frac{output}{\| output \|}
$$

ここでは、torchで正規化しましたが、faiss.normalize_L2を使って正規化することも可能です。ただし、faiss.normalize_L2はnumpy.arrayの入力を想定しているので、変換が必要になります。
# 訓練データの特徴量とラベルを全て抜き出す
model.eval()
features = None
classes = None
for images, labels in tqdm(train_loader):
with torch.no_grad():
images = images.to(device)
outputs = model(images)
outputs = (outputs.transpose(1,0)/outputs.norm(dim=1)).transpose(1,0)
if classes is None:
classes = labels.cpu()
else:
classes = torch.cat((classes, labels.cpu()))
if features is None:
features = outputs.cpu()
else:
features = torch.cat((features, outputs.cpu()))特徴ベクトルの分布を学習させる
FAISSでは、特徴ベクトルの分布を学習させる必要があるようです。
以下のコードで6万件の1%を抽出して、分布の学習を行っています。
# 圧縮のために一部のデータで特徴量の分布を学習させる
train_data = np.array([v for v in features if random.random() < 0.01])
index.train(train_data)FAISSに特徴ベクトルを登録
FAISSに特徴ベクトルを登録します。
登録は、(特徴ベクトル、ベクトルのID)の組みとなります。今回は、正解の数字をIDとして登録しています。
登録したいベクトルがメモリに入りきらない場合は、分割して登録が可能です。
下記の例では、10000個毎に登録を行っています

一気に登録しても良いと思いますが、他のコードが10,000個単位で登録していたので合わせました
# 10000個毎に追加:細切れで追加可能なので、後から追加も可能
batch_size = 10000
for i in range(0, len(classes), batch_size):
input_vecs = []
input_ids = []
for item_id, vec in zip(classes[i:i+batch_size], features[i:i+batch_size]):
input_vecs.append(vec)
input_ids.append(item_id)
input_vecs = np.array(input_vecs, dtype=np.float32)
input_ids = np.array(input_ids, dtype=np.int64)
index.add_with_ids(input_vecs, input_ids)
# 作成したインデックスを保存
faiss.write_index(index, "features.index")インデックスを使った検索
検証データの先頭の64個を使って、近傍探索を行ってみます。
FAISSでは、特徴ベクトルを複数渡せば、全ての特徴ベクトルに対して一気に近傍探索を行なってくれます。
# インデックスを使って近傍検索を行う
# 検証データから最初の64個を取り出して特徴量を生成
images, labels = valid_loader.__iter__().__next__()
model.eval()
with torch.no_grad():
images = images.to(device)
features = model(images)
features = (features.transpose(1,0)/features.norm(dim=1)).transpose(1,0)
# 保存したインデックスを読み込む
index = faiss.read_index("features.index")
D, I = index.search(features.cpu().numpy(), 3) # 近傍3個を取得(D: distance, I: index)
for label, idx, dist in zip(labels, I, D):
print(f"正解={label}, 検索結果(上位3位) = {idx}, 距離={dist}")実行結果は以下になります。同じIDが複数個登録されているので、上位3つが同じIDなのは正常です。
正解と上位3つは大体一致しているので、ベクトル検索はうまく動いていると思われます。ただ、距離が1を超えています。これは、IndexIVFPQで量子化した誤差によるものです。
実行結果
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[1.0112848 1.0077612 1.0076492]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[1.0149219 1.0135362 1.0133244]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0119952 1.0108466 1.0093753]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[1.0442381 1.0100461 1.0092627]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[1.011951 1.0065445 1.006035 ]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0128698 1.0095211 1.0091816]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[1.0130725 1.0105096 1.0068108]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[0.9862113 0.9724981 0.96998906]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[0.73821235 0.7217237 0.71698916]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[1.0110637 1.0048431 1.0021498]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[1.01832 1.0179038 1.0146782]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[1.0123885 1.0107207 1.0086939]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[1.0039049 1.0038358 1.0024631]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[1.0155842 1.015381 1.0143192]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0139121 1.0108563 1.0093565]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[1.0348874 1.022584 1.018144 ]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[1.013133 1.0128137 1.0055907]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[1.0062215 1.0058016 1.0056921]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[0.9381873 0.9310677 0.92985135]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[1.0124083 1.0104305 1.0090622]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[1.0069846 1.0051482 1.0034331]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[0.98950887 0.98841494 0.98809016]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[1.0081508 1.007865 1.0071574]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[1.0168253 1.0145342 1.0138997]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[1.0111705 1.0078593 1.0071822]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[1.0328239 1.0119643 1.0117481]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[1.0117471 1.0114481 1.0074339]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[1.0109996 1.0087136 1.0082805]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[1.024983 1.0143646 1.013449 ]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0150168 1.0129571 1.0126307]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[1.0205708 1.0128456 1.0121055]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0183786 1.0113826 1.0108093]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[1.0165431 1.0116448 1.011054 ]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.99282885 0.98880553 0.9876605 ]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[1.0132325 1.0088286 1.0082101]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[1.0088475 1.0068878 1.0067267]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[1.0090743 1.0086018 1.0062716]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0104479 1.0072266 1.0067306]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[1.0077629 1.0024167 0.9995375]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0112015 1.0063481 1.0063055]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0107355 1.0055771 1.0047877]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[1.0099897 1.0089815 1.0088172]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[1.0100173 1.0090948 1.0086652]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[0.99144083 0.98795927 0.98468274]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[1.0115292 1.0094655 1.0092902]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[1.008086 1.0067391 1.0063572]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0134711 1.010293 1.0088378]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[1.0162716 1.0117159 1.0114152]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[1.0127451 1.0107813 1.0082939]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[1.0196259 1.0132562 1.0113461]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[1.012189 1.0073104 1.0041363]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[1.0086309 1.0083492 1.0065744]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[1.0222877 1.0177711 1.0160176]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[1.0158185 1.0152779 1.0152062]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[1.0051847 1.0051298 1.0048001]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[1.036592 1.0037189 1.0035267]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[1.0164645 1.0139744 1.0115216]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[1.0115336 1.0115317 1.0112466]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[1.0078107 1.007804 1.004904 ]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[1.0122112 1.0018755 1.0015599]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[1.0241902 1.0145307 1.013991 ]
正解=8, 検索結果(上位3位) = [2 2 2], 距離=[0.9244242 0.92310137 0.92120945]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[0.90703785 0.9047355 0.902533 ]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[0.66776216 0.6645771 0.6523212 ]実際に、IndexIVFFlatに変更した場合は、距離は1以下の値となりました。この誤差が問題となるような場合はIndexIVFFlatを使った方がよいと思います。ただ、登録数が多くなってデータベースがメモリに入りきらない場合はIndexIVFPQを使う必要があります。この場合は、検索ミスが発生する場合は、深層距離学習の方のマージンなどを調整する必要がありそうです。
実行結果(IndexIVFFlatを利用した場合)
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[0.99952924 0.99928194 0.99908715]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[0.99378777 0.99326235 0.99274284]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.99961805 0.99951744 0.99949044]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[0.9971335 0.99702716 0.996754 ]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.9986703 0.9983394 0.99784297]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.9995047 0.99918777 0.9990769 ]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.99888855 0.9986027 0.9984232 ]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[0.97554123 0.9601409 0.96006715]
正解=5, 検索結果(上位3位) = [5 5 0], 距離=[0.7626473 0.6791354 0.6155524]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[0.9981068 0.9966761 0.99625266]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[0.9981308 0.99741745 0.996755 ]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[0.99798167 0.9973427 0.9968209 ]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[0.99685013 0.9967559 0.9967554 ]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[0.99856997 0.99840325 0.99831647]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.9996408 0.99943036 0.9994295 ]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[0.99375254 0.99047494 0.98996747]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[0.998902 0.9987205 0.9984665]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[0.9990727 0.99882287 0.99875784]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[0.9432198 0.93736756 0.9372077 ]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.9991193 0.999068 0.99906236]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[0.9959773 0.9953418 0.9950657]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[0.99289453 0.99039066 0.9885714 ]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[0.9986452 0.99821454 0.9977913 ]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[0.9982444 0.99815804 0.99808025]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.9962548 0.99617296 0.99605024]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[0.99709725 0.99684346 0.99684185]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[0.99336475 0.992698 0.99255884]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.9991002 0.9989321 0.99892974]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[0.9981387 0.9980784 0.9980502]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.9985074 0.9979682 0.9975626]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[0.9983761 0.99821776 0.99808764]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.9986087 0.99778295 0.9973522 ]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[0.99770856 0.9972066 0.9970131 ]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.9856928 0.98496276 0.982572 ]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[0.9944702 0.99358046 0.9935135 ]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[0.9963084 0.9957669 0.9947572]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[0.99457026 0.9945236 0.9945164 ]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.9987818 0.9987397 0.99870425]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[0.98950964 0.9865631 0.9864447 ]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.9980126 0.9977291 0.99723214]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.99905026 0.99845207 0.9984474 ]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[0.99642205 0.9962784 0.9958193 ]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.99866253 0.9985052 0.9984052 ]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[0.9765811 0.9749228 0.97472113]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[0.99481887 0.9947231 0.9946922 ]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[0.9948515 0.9945291 0.9940168]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.99686766 0.99589926 0.9958499 ]
正解=2, 検索結果(上位3位) = [2 2 2], 距離=[0.9981902 0.9976374 0.99731016]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.9989048 0.99877465 0.9985844 ]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.99852324 0.99829984 0.99828744]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[0.9987005 0.99815226 0.99813884]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[0.9965932 0.99600536 0.99597585]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[0.99752295 0.9969584 0.9968668 ]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[0.9963589 0.99632007 0.99627835]
正解=6, 検索結果(上位3位) = [6 6 6], 距離=[0.99903196 0.9984025 0.9979573 ]
正解=0, 検索結果(上位3位) = [0 0 0], 距離=[0.9969982 0.9951359 0.9945309]
正解=4, 検索結果(上位3位) = [4 4 4], 距離=[0.9991772 0.99848366 0.9983086 ]
正解=1, 検索結果(上位3位) = [1 1 1], 距離=[0.99930394 0.9990373 0.9990122 ]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[0.99838793 0.99824566 0.99749565]
正解=5, 検索結果(上位3位) = [5 5 5], 距離=[0.9896718 0.98861843 0.987526 ]
正解=7, 検索結果(上位3位) = [7 7 7], 距離=[0.99869096 0.9978197 0.9974151 ]
正解=8, 検索結果(上位3位) = [2 2 2], 距離=[0.9459361 0.94277567 0.9363955 ]
正解=9, 検索結果(上位3位) = [9 9 9], 距離=[0.92212224 0.9047428 0.903527 ]
正解=3, 検索結果(上位3位) = [3 3 3], 距離=[0.7776842 0.7065209 0.67590356]近傍検索した検証データ64個は以下の画像です。最後の3の距離が他と比べて遠いのは、画像を見ても??ではあります。2行目先頭の5のスコアと、最後の3のスコアが似たような感じというのは、感覚的には不思議ですね。
ただ、近傍検索でうまく見つけているようです。

深層距離学習+近傍検索について
クラス分類ではなく、特徴ベクトルを出力するとどんなメリットがあるかというと、未知のクラスの分類が可能になることです。
たとえば、数字に加えて’$’などの手書き文字を入力した場合の特徴ベクトル登録しておけば、クラス分類で学習していない’$’も識別できる可能性があります
このように学習していない画像の識別が可能になります。
応用の例としては、顔認証があります。大量の顔画像で学習しておけば、特徴ベクトルは顔の特徴を表すベクトルとなります。
何枚か顔を撮影してモデルで特徴量に変換し登録しておけば、閾値を超える画像がデータベースにあるかどうか調べることで顔認証が可能です。
このように、特徴ベクトル+FAISSを使うと、学習していないクラスの識別が可能となります。
まとめ
以上、深層距離学習+FAISSで、特徴ベクトルを使った近傍検索を行ってみました。
画像を顔に変えれば顔認証になります。顔認証の基本となる部分が大体理解できた気がします。次は、実際に顔認証のコードを作成してみたいと思います。
顔認証のコード作成を行ってみました。以下の記事を参考にしてください






