2024.07.01 2024.08.27

記事内に商品プロモーションを含む場合があります

擬似ラベリング（Pseudo Labeling）でラベリング対象を選ぶ方法｜エントロピーを活用したアプローチを解説

Aru

半教師あり学習において、ラベルなしデータの中からどのデータを選択し、擬似ラベルをつけて学習データに追加するかを決めるのは非常に難しい問題です。擬似ラベルを付与対象とするデータの選択に悩んでいる方は多いのではないでしょうか。この記事では、情報エントロピーを利用して学習に適したデータを選択するための手法を紹介します。

Contents

擬似ラベル（Pseudo Labeling）とは
情報エントロピーを用いたデータの選択
- 情報エントロピーの計算式
- 実際のコードで確認
まとめ

擬似ラベル（Pseudo Labeling）とは

ディープラーニングでモデルの学習を行う際、ラベル付きのデータが少ないけど、ラベルが付与されていないデータは大量に存在するといったシチュエーションが結構あります。

このような場合に活用できるのが「Pseudo Labeling（擬似ラベリング）」という手法です。

擬似ラベリングは、ラベル付きのデータでモデルを学習し、学習したモデルを使ってラベルなしのデータにラベルを付与し、付与したデータも学習データに加えて再度学習させることで、モデルの精度を向上させる手法です。

この手法の具体的なステップは、以下のように説明できます。

初期モデルを訓練
ラベル付きデータを使って、ベースラインのモデルを訓練します
予測ラベルを付与
ベースラインモデルを使って、擬似ラベルを付与したデータを作成します
ラベル付き＋擬似ラベルを使った学習
ラベル付きデータと、擬似ラベルデータを使ってモデルを訓練します
②と③を繰り返す

上記のように、擬似ラベルを付与したデータを追加して学習を行うことで、ラベル付きのデータが少ない場合でも、モデルの精度を向上させることが可能です。

しかしながら、付与した擬似ラベルの品質が悪いと、逆に精度が悪化することあります。

これに対応するために、以下のように徐々に擬似ラベルの重みを大きくする手法が提案されています。

最初のEPOCHではαを０（ゼロ）に設定しておく
loss計算は、ラベル付き（loss0）と擬似ラベル(loss1)で別々に計算する
擬似ラベルのlossにαを乗算して損失を計算（loss = loss0 + αloss1）
ロス（loss）をbackwardする
EPOCHに応じてαを徐々に1.0にしていく

αを徐々に大きくしていくことで、最初は擬似ラベルを信用せず、学習が進むにつれて擬似ラベルを活用するようになります。

上記の方法でも一定の効果がありそうですが、ラベルなしのデータの中にノイズデータが多い場合は、擬似ラベルを付与したデータが学習の妨げになる可能性があります。

今回紹介する手法は、ラベルなしデータの中から、擬似ラベルをつけるデータを選択する方法です。この手法では、情報エントロピーを用いて、擬似ラベルの良し悪しを判別し、良さそうなものだけに擬似ラベルを付与して学習データに追加することで、精度を向上させるという仕組みです。以下、この手法いついて詳しく解説していきます。

情報エントロピーを用いたデータの選択

情報エントロピーの計算式

情報エントロピーを計算する手順は以下になります。

確率の正規化

与えられたサンプルの確率データから、サンプルの確率の合計が１になる様に正規化します。これは、以下の様な式になります。

$$
p_i = \frac{p_i}{\sum_{i=1}^{N}P_i}
$$

$P_i$は、サンプルのクラスiの確率です。Nはクラスの総数になります。

エントロピーの計算

確率を正規化していれば、エントロピーは以下の式で計算できます。

$$
H = -\sum_{i=1}^{N}p_i \log_2(p_i)
$$

具体的なイメージ

例えば、10クラス分類の場合、モデルの出力は10個の値になります。

まず、あるデータに対するモデルの出力結果が合計が1になる様に正規化します。

確率の正規化は上記式ですが、ディープラーニングのモデルの出力の場合はsoftmaxを使います。

次に、エントロピーを計算します。エントロピーは情報量が多いほど大きな値になります。つまり、クラスが確定できていない（予測が正確でない）ほど、大きな値になります。

したがって、エントロピーが小さいものが予測の精度が高いと考えることができます。

情報エントロピーを利用した擬似ラベリングは、この性質を使って、ラベルなしデータに予測を行い、例えば、「エントロピーが小さい方から10％」などを擬似ラベル付きデータとして採用する方法になります。

実際のコードで確認

MNISTの手書き文字を学習するコードを使って、エントロピー計算を試してみました。

擬似ラベリングまでは試していません

コードは、こちらにあります（Google Colabで実行できます）

このコードでは、まずモデルを学習して、学習していない検証データのエントロピーと、ランダムなデータのエントロピーを比較しています。

エントロピーの計算は以下のコード（Pytorchのテンソル）になります

入力データが、（bacth, クラスの予測結果）になっている前提のコードです。MNISTでバッチサイズを64にした場合は(64, 10)という値が入力されることになります。

def calculate_entropy(probabilities):
    # 各サンプルの確率分布を生成 (softmaxを適用して正規化)
    probabilities = probabilities.softmax(axis=1)
    # エントロピーを計算
    entropy = -torch.sum(probabilities * torch.log2(probabilities + 1e-10), axis=1)
    print("ent" , entropy)

    return entropy

このプログラムでは、先ほどの式をそのまま行っています（確率の正規化はsoftmaxを用いています）

検証データのエントロピー

検証データのエントロピーを計算するコードです。

valid_loader = torch.utils.data.DataLoader(valid_dataset, batch_size=64, shuffle=False)

loader = valid_loader.__iter__()
images, labels = next(loader)

model.eval()
with torch.no_grad():
  outputs = model(images.to(device)).cpu()

# エントロピーを計算
entropy = calculate_entropy(outputs)
print("Label Entropy for each sample in the batch:", entropy)

ent = []
for e in entropy.tolist():
  ent.append([e, 0])

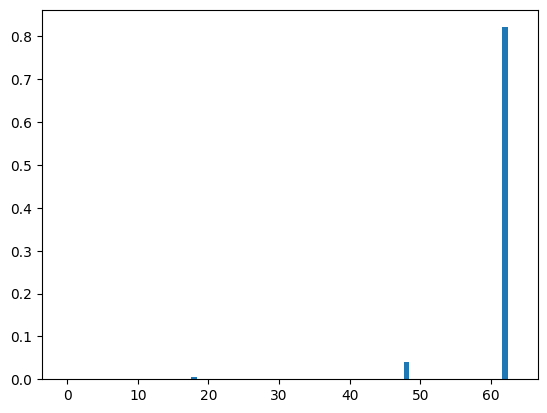
plt.bar(range(len(entropy)), entropy.numpy())
# plt.ylim(0, 1.5)
print(entropy.mean())

ほとんどのデータが0.1以下とかなり小さいことがわかります。

モデルの検証データの精度は0.987なので、ほとんどのデータに予測ができるモデルです。

このように、データの予測が正確な場合はエントロピーが低くなることを確認できました。

なお、１つだけエントロピーの大きなものがありますが、おそらく予測が上手く行っていないデータだと思います。

ランダムデータのエントロピー

検証データでは、エントロピーが小さくなったので、次はランダムな入力データに対するエントロピーを求めてみました。予想では、先ほどよりエントロピーが大きくなるはずです。

noise = torch.randn(images.shape)

model.eval()
with torch.no_grad():
  outputs = model(noise.to(device)).cpu()

# エントロピーを計算
entropy = calculate_entropy(outputs)
print("Label Entropy for each sample in the batch:", entropy)

for e in entropy.tolist():
  ent.append([e, 1])

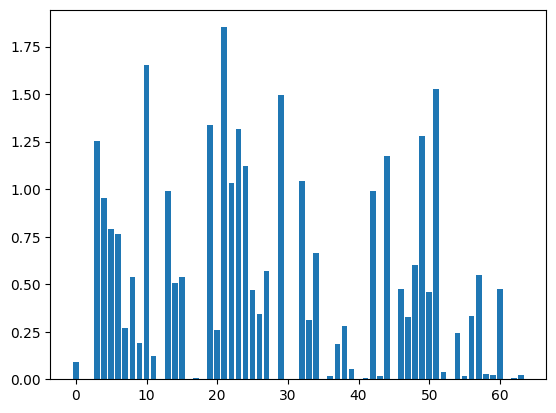
plt.bar(range(len(entropy)), entropy.numpy())
# plt.ylim(0, 1.5)
print(entropy.mean())

上の検証データのグラフをｙ軸のスケールが異なることに注意してください。

こちらを見ると、ほとんどのデータでエントロピーが大きいことがわかります。ランダムデータの予測結果を見ると、予測が正確でない場合はエントロピーが大きくなることを確認できました。

予測結果をエントロピー順にならべた結果

以下は、エントロピーの小さい順に予測結果を並べたものです。

先頭が0:が検証データの結果、1:がランダムデータを表しています。

これを見ると、エントロピーが小さいのは検証データで、上位の10%（12個）にはランダムデータが出現していないことがわかります。つまり、上位10%を擬似ラベリングの候補として選択した場合、学習データとして有用なものが選ばれることが確認できました。

0 : 1.4397987798414765e-15
0 : 1.8694206881282593e-14
0 : 1.965096278245832e-14
0 : 6.398483495427196e-14
0 : 8.42344247196751e-14
0 : 8.796188468362595e-14
0 : 4.072558533897014e-13
0 : 1.460741141760813e-12
0 : 2.1877430422811983e-12
0 : 2.6758228879181223e-12
0 : 1.6119876267151056e-11
0 : 3.251878280541298e-11
0 : 4.4373140578590764e-11
0 : 9.03667488061366e-11
0 : 1.0491833096759606e-10
0 : 1.1842539449080647e-10
0 : 1.289887863187289e-09
0 : 1.643901903491951e-09
0 : 2.1143995443395625e-09
0 : 8.61800941720503e-09
0 : 1.2429514306688816e-08
0 : 1.3408486765342786e-08
0 : 1.8368734089335703e-08
0 : 2.1639149139218716e-08
0 : 2.4494511308148503e-08
0 : 3.308353768716188e-08
0 : 3.898614053809979e-08
0 : 4.052600388604333e-08
0 : 4.483288051915224e-08
0 : 5.3041194547631676e-08
0 : 5.504172762016424e-08
0 : 6.655741913164093e-08
0 : 7.143655977870367e-08
1 : 8.011910068717043e-08
0 : 1.0623269020015869e-07
0 : 1.289848370333857e-07
0 : 1.5738694969513745e-07
0 : 2.682071453818935e-07
0 : 2.7844475880556274e-07
0 : 3.877296421705978e-07
0 : 4.155040755904338e-07
0 : 5.636905484607269e-07
0 : 5.938584877185349e-07
0 : 6.260415261749586e-07
0 : 6.749136787220777e-07
0 : 8.241378282036749e-07
0 : 8.538188467355212e-07
0 : 1.1414081200200599e-06
0 : 1.8244838884129422e-06
0 : 2.479798922649934e-06
0 : 3.1368117561214603e-06
0 : 3.6470817121880827e-06
1 : 4.628553597285645e-06
0 : 5.140829216543352e-06
0 : 7.583244951092638e-06
0 : 8.580634130339604e-06
0 : 9.334750757261645e-06
0 : 1.2113468073948752e-05
0 : 2.9907891075708903e-05
1 : 3.324811768834479e-05
0 : 6.620700878556818e-05
0 : 6.918050348758698e-05
1 : 7.017049938440323e-05
1 : 7.501238724216819e-05
0 : 8.83998436620459e-05
1 : 0.00011605346662690863
1 : 0.00017143985314760357
0 : 0.00018272442684974521
1 : 0.00031971646239981055
1 : 0.0004436223243828863
1 : 0.001999943982809782
1 : 0.003026221413165331
1 : 0.003369639627635479
1 : 0.003706874093040824
1 : 0.005054370034486055
1 : 0.005653219297528267
0 : 0.006303085014224052
1 : 0.007811151444911957
1 : 0.018431825563311577
1 : 0.018557537347078323
1 : 0.019766196608543396
1 : 0.022310111671686172
1 : 0.02238815277814865
1 : 0.02989603579044342
1 : 0.038062743842601776
0 : 0.040340110659599304
1 : 0.0523688942193985
1 : 0.08862651884555817
1 : 0.12048201262950897
1 : 0.18537549674510956
1 : 0.19311237335205078
1 : 0.24176770448684692
1 : 0.25910088419914246
1 : 0.27074134349823
1 : 0.27767881751060486
1 : 0.31421369314193726
1 : 0.32982635498046875
1 : 0.3316098153591156
1 : 0.3444872498512268
1 : 0.4606854319572449
1 : 0.46765342354774475
1 : 0.47343525290489197
1 : 0.4763234853744507
1 : 0.5054986476898193
1 : 0.5371925234794617
1 : 0.5398625731468201
1 : 0.5493469834327698
1 : 0.5675762891769409
1 : 0.5994760990142822
1 : 0.6632948517799377
1 : 0.7625812292098999
1 : 0.7926285862922668
0 : 0.8214751482009888
1 : 0.9545555114746094
1 : 0.9900473952293396
1 : 0.9923519492149353
1 : 1.0342304706573486
1 : 1.0404163599014282
1 : 1.119917631149292
1 : 1.1737388372421265
1 : 1.253156304359436
1 : 1.2796330451965332
1 : 1.315953016281128
1 : 1.3363745212554932
1 : 1.4950650930404663
1 : 1.52500319480896
1 : 1.6531705856323242
1 : 1.8516978025436401

以上のように、情報エントロピーを利用することで、擬似ラベルの正確性をある程度判断することができそうです。