MENU
プログラミング
記事内に商品プロモーションを含む場合があります

競技プログラミングで使うトライ木（Trie）実装メモ（Python / Go）

Aru

最近、AtCoderのABC（AtCoder Beginner Contest）を解いていて、トライ木（Trie）を使う問題に何度かでくわしました。毎回悩むので、アルゴリズムを整理するために、ブログにまとめました。

Contents
  1. トライ木（Trie）とは
  2. 実装してみる（Python）
  3. 使ってみる
  4. Goでの実装
  5. まとめ

トライ木（Trie）とは

トライ木（Trie）は、有向グラフ（厳密には有向木）の一種で、主に文字列の集合を管理するためのものです。トライ木は「接頭辞木（Prefix Tree）」とも呼ばれます。

トライ木は、ノード自体にキー全体（文字列そのもの）を保存するのではなく、ルートからそのノードまでの経路（エッジのラベル）によって文字列を表すのが特徴です。

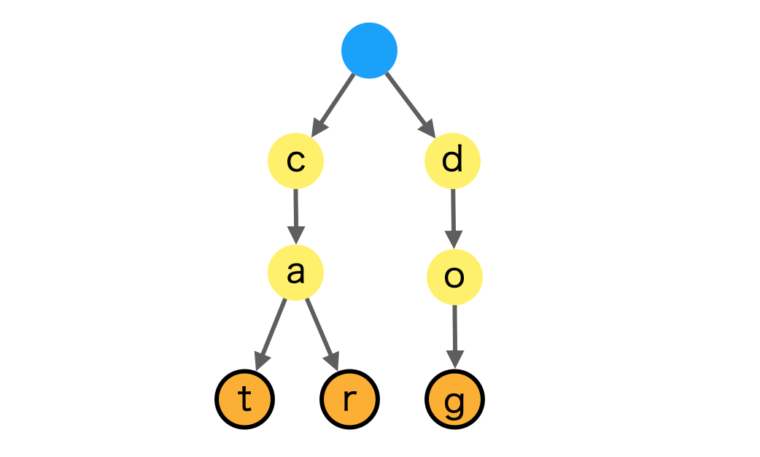
例えば、「cat」「car」「dog」という単語を格納する場合、以下のような構造になります。途中の文字と終端（単語の終わり）の文字には印がつけられていて、この印（マーク）により終端を区別します。この例では、catの”t”、carの”r”,dogの”g”のノードに終端マーク（図ではオレンジのノード）がついています。

トライ木の特徴をまとめると以下のようになります。

  1. 共通接頭辞の共有
    “cat”と”car”のように、”ca”までが共通していれば、その部分のノードは共有される
  2. 高速な検索
    文字列の長さが $L$ のとき、要素数 $N$ に関わらず $O(L)$ の計算量で検索・追加が可能。共通の接頭辞を持つ単語の列挙を高速に行える

実装してみる（Python）

今回はPythonの標準機能である dict（辞書型）を使って、各ノードの子ノードを動的に管理する方法を採用しました。固定長の配列（サイズ26など）を使う実装と比較して、出現する文字の種類に制限がないし、直感的です。

データ構造

まずはノードを表す TrieNode クラスと、木全体を管理する Trie クラスを定義します。

class TrieNode:
    def __init__(self):
        # 辞書型の定義、キー: 文字, 値: 子ノード(TrieNode)
        self.children = {}
        # そのノードが単語の終わりかどうかを表すフラグ
        self.is_end_of_word = False

class Trie:
    def __init__(self):
        self.root = TrieNode()

文字列の追加

ルートから文字列を一文字ずつ辿り、ノードが存在しなければ新規作成していきます。最後の文字に到達した場合、そのノードの is_end_of_word を True にします。

    def insert(self, word: str) -> None:
        """文字列を追加する"""
        node = self.root
        for char in word:
            if char not in node.children:
                node.children[char] = TrieNode()
            node = node.children[char]
        node.is_end_of_word = True

文字列の検索

ルートから順に辿っていきます。途中でパスが途切れたらその単語は存在しません。また、最後まで辿り着いたとしても、is_end_of_word が True でなければ（例えば “apple” が登録されている時の “app” の検索など）、登録されている単語でないことに注意が必要です

    def search(self, word: str) -> bool:
        """完全一致検索"""
        node = self.root
        for char in word:
            if char not in node.children:
                return False
            node = node.children[char]
        return node.is_end_of_word

文字列の削除

削除処理は真面目にやると複雑（不要になったノードを再帰的に削除するなど）ですし、競技プログラミングではあまり見かけません。今回は、単純にフラグを落とすだけの処理（論理削除）にしたいと思います。

メモリ効率を考えると、きちんと削除したほうが良いです。この場合は、再帰関数を使うと楽です

    def delete(self, word: str) -> bool:
        """文字列を削除する（フラグを落とすだけの論理削除）"""
        node = self.root
        for char in word:
            if char not in node.children:
                return False  # 単語が存在しない
            node = node.children[char]
        
        if not node.is_end_of_word:
            return False  # そもそも登録されていない
            
        node.is_end_of_word = False
        return True

文字列を辞書順で取り出す

深さ優先探索（DFS）を行うことで、登録されている全単語を辞書順（昇順）に取り出すことができます。条件に合わせた、文字列を構成しつつ辞書順で出力する場合に便利です。

    def get_all_words_sorted(self) -> list[str]:
        """辞書順に全単語を取得する"""
        results = []
        
        def _dfs(node: TrieNode, prefix: str):
            if node.is_end_of_word:
                results.append(prefix)
            
            # 辞書順にするためにキーをソートして走査
            for char in sorted(node.children.keys()):
                _dfs(node.children[char], prefix + char)
                
        _dfs(self.root, "")
        return results

プログラム全体

トライ木のクラス定義全体です。そのままコピペで使えます。

class TrieNode:
    def __init__(self):
        # 辞書型の定義、キー: 文字, 値: 子ノード(TrieNode)
        self.children = {}
        # そのノードが単語の終わりかどうかを表すフラグ
        self.is_end_of_word = False

class Trie:
    def __init__(self):
        self.root = TrieNode()


    def insert(self, word: str) -> None:
        """文字列を追加する"""
        node = self.root
        for char in word:
            if char not in node.children:
                node.children[char] = TrieNode()
            node = node.children[char]
        node.is_end_of_word = True

    def search(self, word: str) -> bool:
        """完全一致検索"""
        node = self.root
        for char in word:
            if char not in node.children:
                return False
            node = node.children[char]
        return node.is_end_of_word
    
    def delete(self, word: str) -> bool:
        """文字列を削除する（フラグを落とすだけの論理削除）"""
        node = self.root
        for char in word:
            if char not in node.children:
                return False  # 単語が存在しない
            node = node.children[char]
        
        if not node.is_end_of_word:
            return False  # そもそも登録されていない
            
        node.is_end_of_word = False
        return True


    def get_all_words_sorted(self) -> list[str]:
        """辞書順に全単語を取得する"""
        results = []
        
        def _dfs(node: TrieNode, prefix: str):
            if node.is_end_of_word:
                results.append(prefix)
            
            # 辞書順にするためにキーをソートして走査
            for char in sorted(node.children.keys()):
                _dfs(node.children[char], prefix + char)
                
        _dfs(self.root, "")
        return results

使ってみる

実装したクラスを利用する例です。

trie = Trie()

# 文字列の追加
words = ["cat", "car", "dog"]
print(f"追加する単語: {words}")
for w in words:
    trie.insert(w)

print("-" * 20)

# 検索テスト
print(f"Search 'cat': {trie.search('cat')}") 
print(f"Search 'dog': {trie.search('dog')}")
print(f"Search 'do': {trie.search('do')}") 

print("-" * 20)

# 辞書順リストアップ
print("辞書順の単語リスト:")
print(trie.get_all_words_sorted())

print("-" * 20)

# 削除テスト
print("Delete 'car'")
trie.delete("car")
print(f"Search 'car': {trie.search('car')}") 
print(f"Search 'cat': {trie.search('cat')}") 

print("-" * 20)
print("削除後の単語リスト:")
print(trie.get_all_words_sorted())

Goでの実装

私自身、Go言語を頻繁に使うので、Go言語での実装も最後に追加しておきます。プログラムはコピペして利用しやすいようにしています（packageを分けることでライブラリ化も可能です）。

package main

import (
	"fmt"
	"sort"
)

type TrieNode struct {
	children    map[rune]*TrieNode
	isEndOfWord bool
}

func newTrieNode() *TrieNode {
	return &TrieNode{
		children:    make(map[rune]*TrieNode),
		isEndOfWord: false,
	}
}

type Trie struct {
	root *TrieNode
}

// NewTrie は新しいTrieを作成します
func NewTrie() *Trie {
	return &Trie{
		root: newTrieNode(),
	}
}

// Insert は単語を追加します
func (t *Trie) Insert(word string) {
	node := t.root
	for _, char := range word {
		if _, ok := node.children[char]; !ok {
			node.children[char] = newTrieNode()
		}
		node = node.children[char]
	}
	node.isEndOfWord = true
}

// Search は完全一致検索を行います
func (t *Trie) Search(word string) bool {
	node := t.root
	for _, char := range word {
		if _, ok := node.children[char]; !ok {
			return false
		}
		node = node.children[char]
	}
	return node.isEndOfWord
}

// StartsWith は指定した接頭辞で始まる単語があるか確認します
func (t *Trie) StartsWith(prefix string) bool {
	node := t.root
	for _, char := range prefix {
		if _, ok := node.children[char]; !ok {
			return false
		}
		node = node.children[char]
	}
	return true
}

// GetAllWordsSorted は辞書順に全単語を取得します
func (t *Trie) GetAllWordsSorted() []string {
	var results []string
	var dfs func(node *TrieNode, currentStr string)

	dfs = func(node *TrieNode, currentStr string) {
		if node.isEndOfWord {
			results = append(results, currentStr)
		}

		// キーをソートして順序を保証する
		keys := make([]int, 0, len(node.children))
		for k := range node.children {
			keys = append(keys, int(k))
		}
		sort.Ints(keys)

		for _, k := range keys {
			char := rune(k)
			dfs(node.children[char], currentStr+string(char))
		}
	}

	dfs(t.root, "")
	return results
}

func main() {
	t := NewTrie()

	t.Insert("apple")
	t.Insert("app")

	fmt.Println(t.Search("apple")) // true
	fmt.Println(t.Search("app"))   // true
	fmt.Println(t.Search("ap"))    // false

	fmt.Println(t.GetAllWordsSorted()) // [app apple]
}

まとめ

トライ木を使う問題が、ちょくちょく出題されています。ABC437-E問題なども、トライ木の問題です。ただし、実装自体は少し工夫が必要（木の構築に工夫が必要）な問題も多いので、アルゴリズムを理解して、自分で実装できるようにしておくと良いです。

基本的には、１文字（あるいは一要素）ごとに繋がった木構造を構築するものですし、辞書順探索は、DFS（深さ優先探索）で可能だということを理解しておけば良いかと思います。

個人的には「この問題、トライ木で解ける！」と気づけることが大切で、知識としてトライ木の用途を理解していることが重要かなと思っています

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

ABOUT ME
ある/Aru
ある/Aru
IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)
Contact
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
Recommend
こちらの記事もどうぞ
記事URLをコピーしました