AtCoderのABCで詰まった時の思考(解法)のヒント(助け)

AtCoderで問題を解いている時に解法に困った時は、視点を変えてみることが大切だと思います。この記事は、特にABC問題を解く上で役立つ考え方や視点を提供するための解法のヒントです。同じように、困っている方、問題を解く糸口を探している方の助けになればと思います。
その他のAtCoderに役立つ記事の一覧は以下にあります。

はじめに
この記事のコンセプトは、「AtCoderの問題を解いていて解法が思い浮かばない場合に眺める記事」です。
解法を考える上で大切なのは、問題文の中にあるヒントですが、自身が問題を解く時に考えているいろいろなポイントを記事にしてみました。
私自身、まだ水色なので、そこまで実力があるわけではないですが、どんな感じで考え、どのように解法を考えているかのヒントになれば幸いです。
競技中に、解法に詰まった時に、ざっと眺めてもらえば解法のヒントがあるかもしれませんので活用してください。

とりあえず、発想を転換するために、眺めてみてください。解法を思いつくかもしれません。
制約から考察する
制約とは
制約とは、問題に書かれている変数の範囲などの制約です。この制約には、解法に至るヒントが隠れています。
制約がすごく小さい
例えば、1 < N < 10みたいにすごく小さい場合は、全探索が候補になります。
全パターンを試してみる
Beginner ContestのA, B問題であれば、単純に全パターンを試すだけのことがあります。とりあえず、素直に実装する方法を考えます
要素を使う・使わないなどの場合
使う・使わないは0と1の2値で表すことができます。それが10個であれば2^10=1024通りのパターンですので全探索可能です(ビット全探索)。以下のようなコードで探索できます。
for i in range(1<<N) :
for j in range(N):
if i>>j%2 == 1 : 使うものを追加
使うものだけで処理した結果を計算制約がすごく大きい
例えば、$10^{18}$みたいな値です。このような制約の変数は、以下のように考えます
- ループは無理
- 配列確保も無理
- 乗算がありそうな場合は、オーバーフローに気をつける必要がある
ということで、ループが必要な場合は全体をループするのは難しく、配列を確保するのも難しいのでこれらのアプローチはないことになりあす。
値の範囲は$10^{18}$だけど、個数が10万個くらいの場合
値の範囲は大きいけど、変数の数(個数)は10万個程度の場合は、個数が少ないのを利用した解法の可能性が高いです。
まず、辞書型や集合型で解けるかどうか考えてみます。
「値の範囲が10^5くらいなら解法が思いつくのに」というパターンの場合、範囲を圧縮することで解ける可能性があります。例えば、大小関係だけが重要な場合は範囲を圧縮できる可能性があります。数(N)が少なければ、圧縮すれば配列に収まります。
圧縮のコード例
下記のコードで、aの座標圧縮した結果がbに格納されます。
a = list(map(int, input().split())
tbl = {v:i for i, v in enumerate(list(set(a)))}
b = [tbl[e] for e in a]
aをsetで集合型にして重複を削除し、tbl[x] = idxのテーブルを作成。aをidxに変換した値をbに格納しています。
設問のパターンから考察する
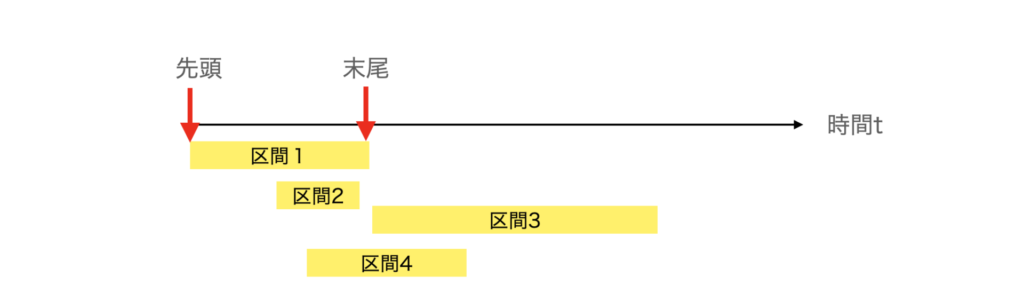
区間がたくさんある場合
現在時刻を管理しながら手前から処理していく方法が考えられます。未処理のものを優先キューにいれれば、手前から処理できます。

時間区間の場合は、区間終わりの時間、または区間始まりの時間のどちらが重要そうか考えます。
グラフで表現できそう
グラフで表現できそうな場合は、幅優先探索(bsf)、深さ優先探索(dfs)、ダイクストラ法で解けそうか考えてみる。
閉路のない有向グラフ(DAG)表現が可能かどうかも考えるポイントになります。DAGであれば、解法があったりします。

H, Wのマス目
以下を検討してみる
- グラフで解けそうか→経路探索
- 上から順番に決められそうか→動的計画法
横・縦のどちらかが極端に小さい場合はbit表現も視野に入れる - 縦・横を独立で処理できそうか→縦・横を別で考える
漸化式で表現できそう
漸化式で表現できそうならDP(動的計画法)ができないか考える。ポイントは、
- 配列として持てるサイズになるか
- ループさせたときに$10^7$~$10^8$くらいの演算量になりそうか
の2点。
Q個の処理を逐次で行うパターン
最初から処理するのではなく、最後から逆にやる方法や、ソートして行う方法など、順番を変えたら簡単に解けないか考えてみます。
順番を変更したら解けそうな場合は、処理内容を一度記録しておいて、順番を入れ替えて処理してみます。
ループを減らせそうか考察する
最内ループを減らせないか
「a+b+c = N」になるa,b,cの組みを求める問題の場合、aとbが決まればcは自動的に決まります(c = N-a-b)。すると3重ループのコードは2重ループに書き換えることができます。
cnt = 0
for a in range(1, N+1):
for b in range(1, N+1):
for c in range(1, N+1) :
if a+b+c == N : cnt += 1
print(cnt)cnt = 0
for a in range(1, N+1):
for b in range(1, N+1):
c == N - a - b
if 1<=c and c <= N : cnt+=1
print(cnt)こんな感じでループ数を減らせないか考えます。ABC(Atcoder Beginner Contest)のA, Bくらいのレベルなら、この手の発想で解けることがあります。
例えば、2つの要素の合計の総和などを求める問題は以下の記事のようなアプローチがあります。

尺取り法が使えないか
例えば、区間最大和などは以下の方法で解くことができます。

このように尺取り法で解けないかを考えるのも1つの方法です。範囲内の値が単調増加な場合の区間和などは尺取り法が使える可能性が高いです。
まとめ
とりあえず、思いつくものを書き出してみました。問題を解いていてきづいたら都度書き足していきたいと思います。
競技プログラミングを楽しみましょう。





