次元圧縮|PCA, t-SNE, UMAPで高次元データを可視化する【初級 深層学習講座】

次元圧縮(次元削減)は、データの可視化や解析を行うための重要な技術です。この記事では、次元圧縮の代表的な手法であるPCA、t-SNE、UMAPを用いて、高次元データを可視化する方法について解説します。
高次元データを可視化する
機械学習やディープラーニングでは、入力や出力されたデータが高次元となることが多いです。例えば、画像のクラス分類のタスクのネットワークの最終層手前の特徴量は数百から数千次元になることは少なくありません。
次元圧縮はこのような高次元データを低次元に変換し、直感的に理解しやすい形で可視化する方法です。代表的な手法には、主成分分析(PCA)、t-SNE、UMAPなどがあります。
仮に、100次元の特徴量を持つデータがあるとします。100次元のデータをそのままグラフにプロットすることは難しく、また、プロットしたとしても直感的に理解することはできません。
このような高次元データを可視化する方法として、次元圧縮があります。
次元圧縮は高次元データを低次元に変換するもので、データの特徴を保持したまま次元を少なくすることで、グラフ化したり、データの特徴やパターンを人が理解する助けになります。
データを可視化してデータの特徴が把握できれば、モデルのトレーニングや結果の解釈にも役立ちます。このように、データの次元圧縮は機械学習やディープラーニングにとって有効な解析手段の一つです。
この、代表的な次元圧縮手法としては、主成分分析(PCA)、t-SNE、UMAPなどがあります。
高次元のデータを、「重要な情報を保持したまま」低次元データに変換する手法のこと。主に、データの特徴の可視化のために用いられる。また、低次元に変換したデータを特徴量として利用することもある。
この記事では、次元圧縮の手法としてメジャーなPCA、t-SNE, UMAPをPythonで利用する方法について解説します。

アルゴリズムについては詳しく解説せず、主にライブラリを使った変換方法について解説します
評価に利用するデータセット
評価の前に、データセットを用意します。ここでは、scikit-learnのデータセットジェネレータを使ってデータセットを作成します。
ライブラリのインストール
必要なライブラリをインストールします
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import make_classificationデータセットの作成
データセットはmake_classificationを利用して作成します。
make_classificationについては以下の記事を参考にしてください


作成するデータは特徴量が20(n_features=20)の、全部で1000個のデータからなるデータセットです(n_samples=1000)。
クラス数は3つで、各クラスは1つの塊(クラスタ)から構成されていることにします(n_clusters_per_class=1)。
なお、20ある特徴量のうち5つがクラス分類と相関の高い特徴量です(n_informative = 5)
X, y = make_classification(n_samples=1000,
n_features=20,
n_informative=5,
n_classes=3,
n_clusters_per_class=1,
random_state=42)
df = pd.DataFrame(X)
df['target'] = y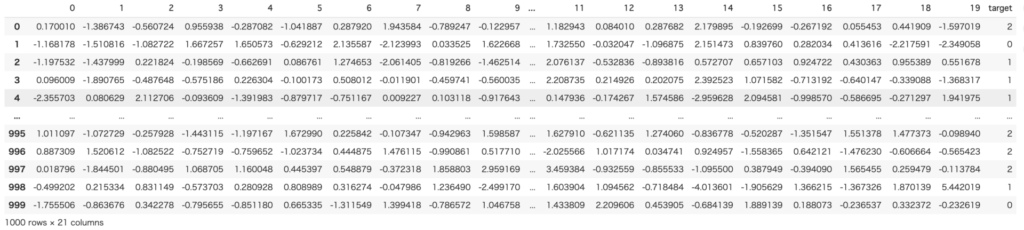
この人工的に生成したデータを各手法で、次元削減していきたいと思います
各手法の使い方
PCA(Principal Component Analysis)
PCA(主成分分析)は、データの分散が最大となる方向に次元を変換する線形次元削減手法です。元のデータセットの特徴を保持しつつ、データセットをより少ない次元で表現することができます。
PCAのメリットは、計算が高速で解釈が容易なことです。一方、線形変換なため、複雑な非線形なデータ圧縮ができないことがデメリットになります。
主成分分析は、統計学でお馴染みの手法なので知っている方も多いと思います。
以下、コードです。PCAはscikit-learnのライブラリに関数として用意されているので、それを利用します。
下のコードでは、n_componentsに2を指定しているので、出力結果は2次元のデータになります。
from sklearn.decomposition import PCA
pca = PCA(n_components=2, random_state=42)
X_pca = pca.fit_transform(X)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y)
plt.show()結果は以下になります。色の違いが3つのクラスの違いになります。ある程度、分離されていますが、混じり合う部分も大きいです。
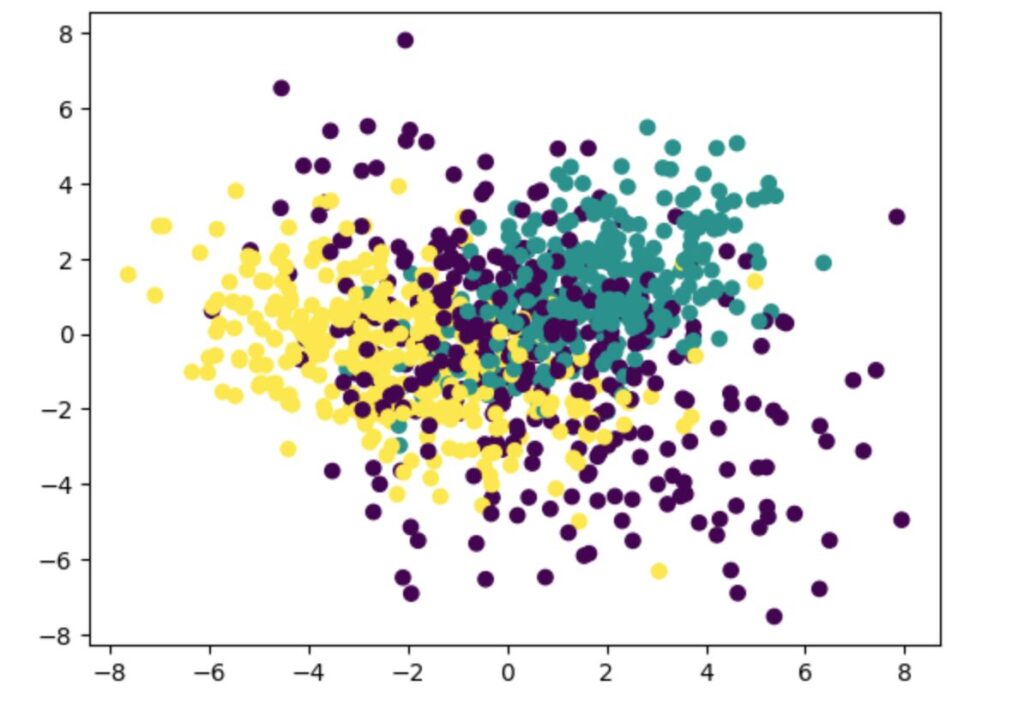
n_informative=5とクラスと相関の高い軸を5つ設定したので、2次元でうまく表現できなかった可能性が高いです。ちなみに、n_informative=2としたデータであれば、もっと綺麗に次元圧縮できました。
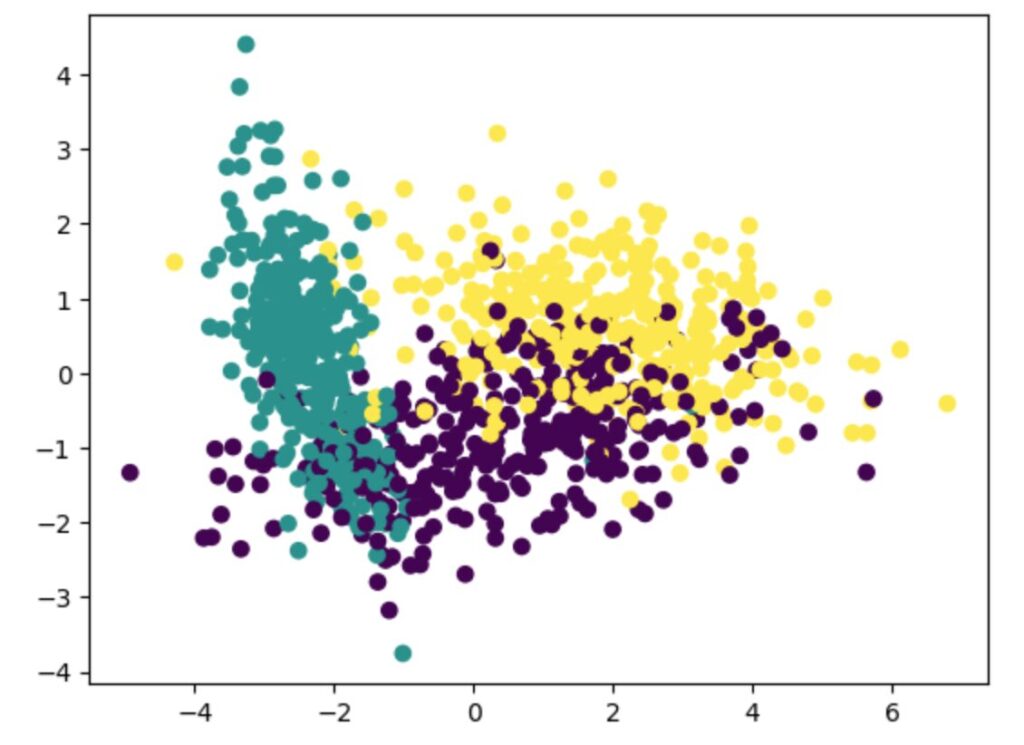
n_informative=2の場合のPCAの結果
t-SNE
t-SNE(t-distributed Stochastic Neighbor Embedding)は、高次元のデータを低次元に圧縮して可視化する目的でよく利用される手法です。高次元データのクラスタ構造を低次元で視覚化するのに適していますが(メリット)、計算コストが高いという欠点(デメリット)があります。
t-SNEの論文のリンク: Visualizing Data using t-SNE
以下、コードです。PCAもscikit-learnのライブラリに関数として用意されているので、それを利用します。
下のコードでは、n_componentsに2を指定しているので、出力結果は2次元のデータになります。
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X)
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y)
plt.show()「計算コストが高いという欠点があります」の通り、少し計算に時間がかかります。しかしながら、PCAと比較して各クラスが綺麗に分離しています。可視化に向いているというのは、嘘ではなさそうです。
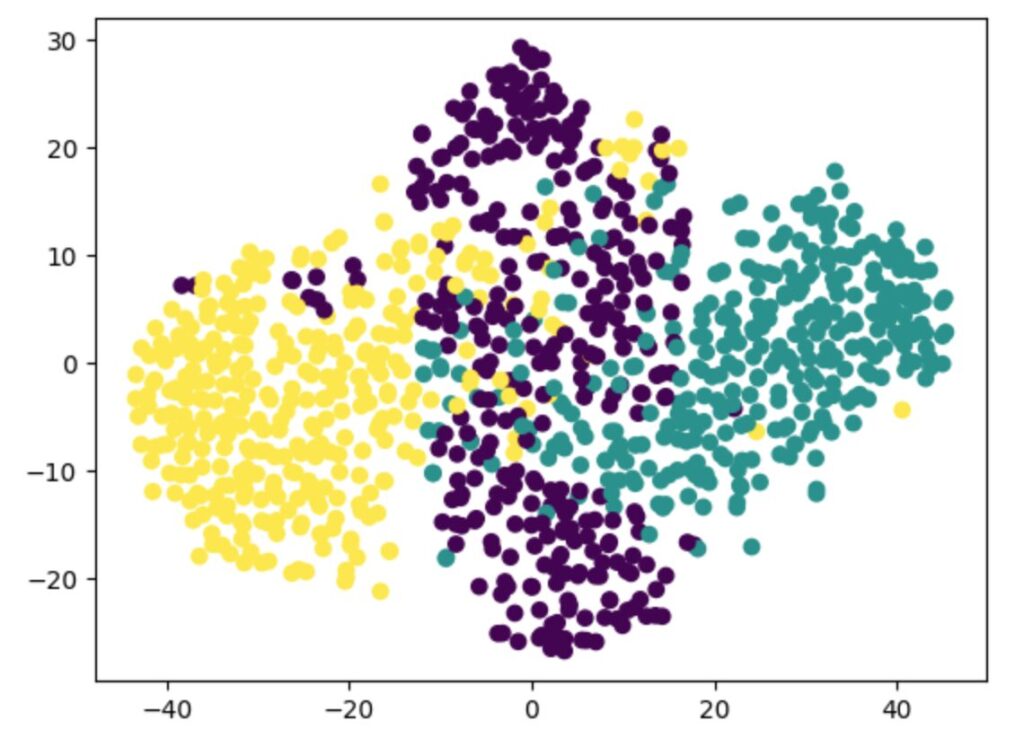
UMAP
UMAP(Uniform Manifold Approximation and Projection)は、高次元データの局所的および大域的な構造を保持しながら低次元表現を生成する手法です。比較的新しく提案された手法で、t-SNEに比べて計算が速く、柔軟性が高いという特徴(メリット)があります。
umapはライブラリをインストール必要があります。ライブラリのインストールは以下のコマンドで行うことができます。
pip install umap-learn以下、UMAPを利用するコードです。
下のコードでは、n_componentsに2を指定しているので、出力結果は2次元のデータになります。
import umap
umap = umap.UMAP(n_components=2, random_state=0)
X_umap = umap.fit_transform(X)
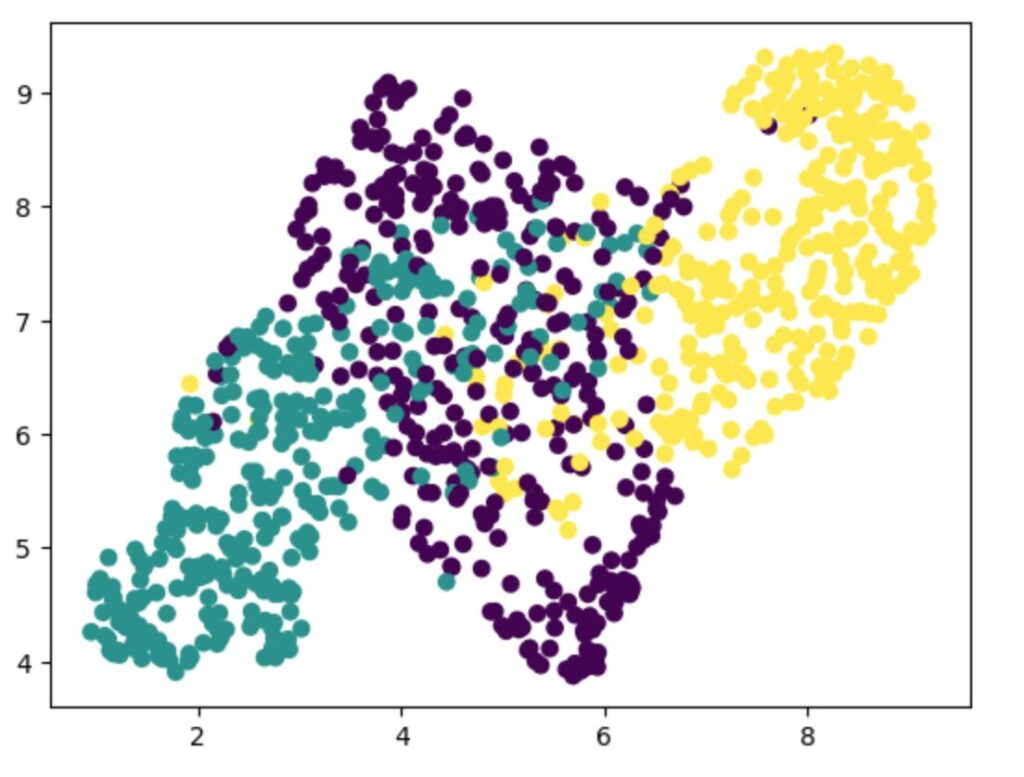
plt.scatter(X_umap[:, 0], X_umap[:, 1], c=y)
plt.show()t-SNEと同様に3つのクラスの分布が分かれています。速度もt-SNEと比べて高速です。
その他注意点
次元圧縮は、各次元のデータの範囲などの影響も受けます。
なので、PCA, t-SNE, UMAPを使った次元削減を行う前に正規化などの処理を行った方が良い結果が得られる場合があります。

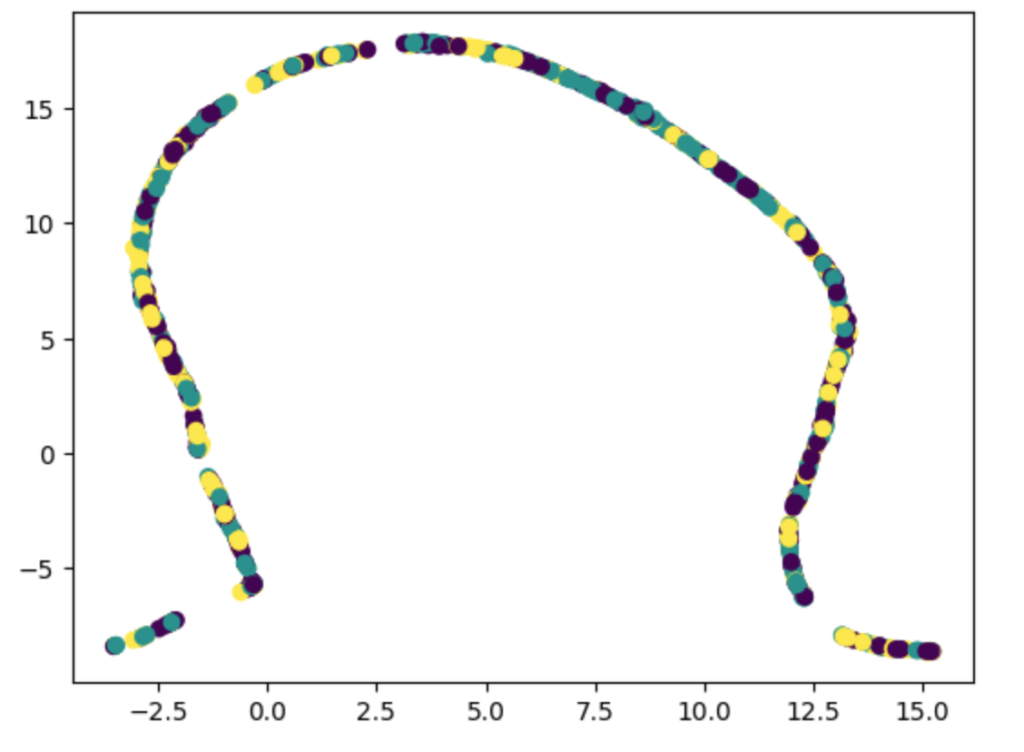
以下の例は、特徴量の1つを100倍した場合のUMAPの結果です。極端にデータ範囲の異なる列があるとそれに引きずられて、うまく次元削減できないことがあります。こういう場合は、UMAPで処理する前に正規化してみましょう。
ライブラリを使うメリット
サンプルのプログラムを見ればわかるように、PCA, t-SNE, UMAPのコードはほぼ同じです。ですから、簡単に手法を変えて評価することができます。
評価の段階で、どれを使うか迷ったらとりあえあず、入れ替えてみることをお勧めします。
結局、可視化して確認するのは「人」ですので、データを可視化してみやすい手法を選びましょう。

高次元になるとt-SNEは遅いので、速度も考えて選択すべきだと思います。個人的にはUMAPを使うことが多いです。
まとめ
以上、高次元データを低次元に圧縮して可視化する手法について解説しました。結構手軽にすることが可能なので、ぜひ試してみてください。








