MENU
初級ディープラーニング
記事内に商品プロモーションを含む場合があります

活性化関数（Activation Function）って何？代表的な関数を紹介【初級 深層学習講座】

Aru

この記事では、ディープラーニングのネットワークを理解するために必要な「活性化関数」について解説します。また、いくつかの代表的な活性化関数を紹介します。

Contents
  1. 活性化関数（Activation Function）とは
  2. 代表的な活性化関数
  3. どの活性化関数が良いの？
  4. まとめ

活性化関数（Activation Function）とは

ニューラルネットワークの活性化関数（Activation Function）は、各ニューロンの出力する際の変換に利用される関数です。

基本的に、ニューロンはy = wx + bという線形変換を行いますが、これだけでは層を増やしても、全体としては単純な線形モデルにしかなりません。

XORの例

例えばXOR（排他的論理和）の問題を考えます。XORの入力と出力は以下のようになります。

x1x2XOR(x1, x2)
000
101
011
111

XORでは、x1とx2のどちらか一方だけ１の時に出力が１、同じ場合は０になります。これを平面上にプロットすると以下のようになります。

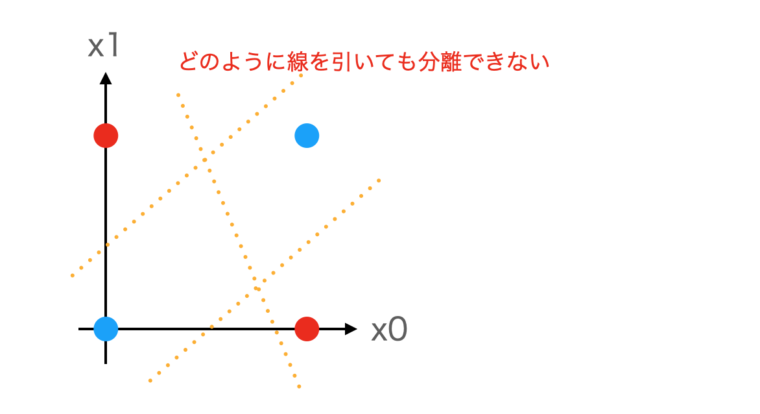
上図を見てわかるように、どんな直線を引いても線形な境界線（直線）では、青と赤の２つの点を分離することはできません。

もし、ニューラルネットに活性化関数がなく、単純な線形変換だけでこの問題を解こうとしても、ネットワーク全体も線形であるため解くことはできません。

そこで、活性化関数として非線形な関数を用いることで、ニューラルネットワークが非線形な境界を学習できるようにします。活性化関数を用いることで、XORのようなパターンでもデータを分離することができるようになります。

非線形性がない場合、ニューラルネットワークは単純な線形変換しか学習できません。活性化関数の存在がディープラーニングでは必要不可欠です。

下図のように、線形だと直線でしか分離できないですが、非線形だと曲線で分離できるようになりますね

線形と非線形のイメージ図（イメージです）

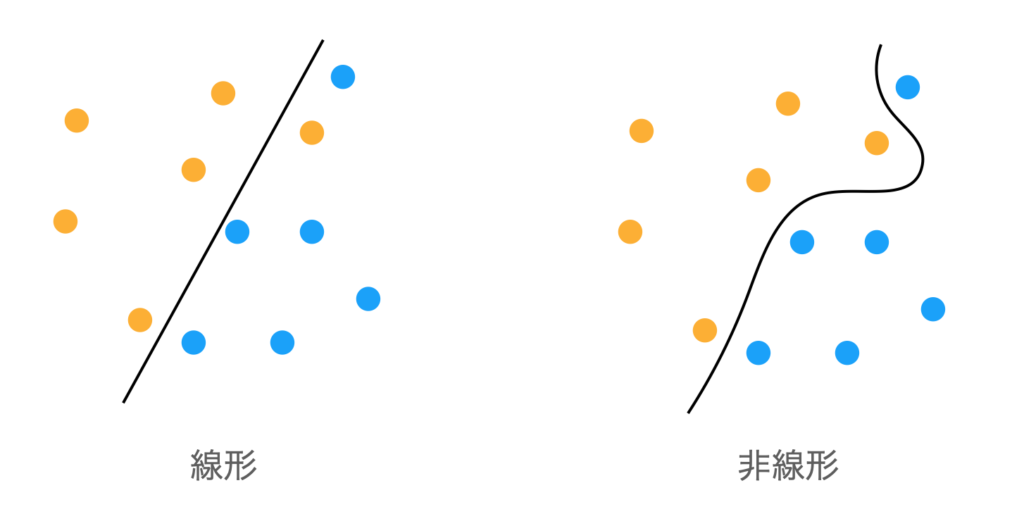
非線形な関数を途中に挟むことで、複雑な分類を学習できるようにしているわけです。

活性化関数を使ったXORを解くネットワーク（具体例）

以下XORを解くニューラルネットの具体的な重みです。２層構造のニューラルネットワークで重みは以下のようになります。

1層目の重みとバイアス

  • ユニット1: z1 = w11 * x1 + w12 * x2 + b1
    • w11 = 10, w12 = 10, b1 = -5
  • ユニット2: z2 = w21 * x1 + w22 * x2 + b2
    • w21 = -10, w22 = -10, b2 = 15

活性化関数（シグモイド関数）

  • シグモイド関数: f(z) = 1 / (1 + exp(-z))

2層目（出力層）の重みとバイアス

  • y = w31 * f(z1) + w32 * f(z2) + b3
    • w31 = 10, w32 = 10, b3 = -15

各入力に対する計算

  1. 入力: (x1 = 0, x2 = 0)
    • z1 = 10 * 0 + 10 * 0 + (-5) = -5
    • z2 = -10 * 0 + -10 * 0 + 15 = 15
    • f(z1) = 1 / (1 + exp(5)) ≈ 0.0067
    • f(z2) = 1 / (1 + exp(-15)) ≈ 0.9999997
    • y = 10 * 0.0067 + 10 * 0.9999997 + (-15) ≈ -4.933
    • 出力 ≈ 0
      yにシグモイドをかけた結果。シグモイドでは、出力が0に近い値になる
  2. 入力: (x1 = 0, x2 = 1)
    • z1 = 10 * 0 + 10 * 1 + (-5) = 5
    • z2 = -10 * 0 + -10 * 1 + 15 = 5
    • f(z1) = 1 / (1 + exp(-5)) ≈ 0.9933
    • f(z2) = 1 / (1 + exp(-5)) ≈ 0.9933
    • y = 10 * 0.9933 + 10 * 0.9933 + (-15) ≈ 4.866
    • 出力 ≈ 1
  3. 入力: (x1 = 1, x2 = 0)
    • z1 = 10 * 1 + 10 * 0 + (-5) = 5
    • z2 = -10 * 1 + -10 * 0 + 15 = 5
    • f(z1) = 1 / (1 + exp(-5)) ≈ 0.9933
    • f(z2) = 1 / (1 + exp(-5)) ≈ 0.9933
    • y = 10 * 0.9933 + 10 * 0.9933 + (-15) ≈ 4.866
    • 出力 ≈ 1
  4. 入力: (x1 = 1, x2 = 1)
    • z1 = 10 * 1 + 10 * 1 + (-5) = 15
    • z2 = -10 * 1 + -10 * 1 + 15 = -5
    • f(z1) = 1 / (1 + exp(-15)) ≈ 0.9999997
    • f(z2) = 1 / (1 + exp(5)) ≈ 0.0067
    • y = 10 * 0.9999997 + 10 * 0.0067 + (-15) ≈ -4.933
    • 出力 ≈ 0

このように、活性化関数を使うことで、非線形なXOR問題を正しく解くことができました。

下図は表計算ソフトで演算した結果です。

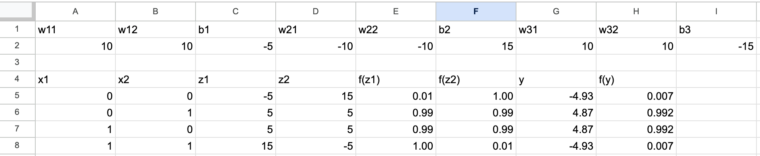
等高線にすると以下のようになります。(0,0)と(1,1)がゼロになるように分割できていることがわかります。

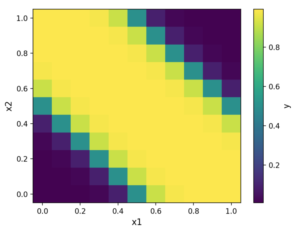
代表的な活性化関数

数十年前は、シグモイドとTanh関数くらいしか活性化関数はありませんでしたが、最近はいろいろな活性化関数が提案され、活用されています。

PyTorchなどでは、さまざまな活性化関数が用意されているので関数を呼び出すだけで利用することができます。

以下、よく使われる活性化関数です。

確認用のコードも合わせて用意しました。なお、動かすには、以下のライブラリをインポートしてください。

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

シグモイド（Sigmoid）

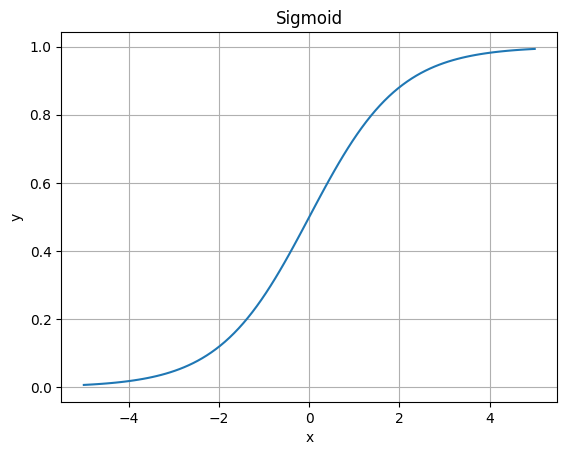
入力を0から1の範囲に変換する活性化関数です。昔から使われている活性化関数ですが、勾配消失の問題があるため、最近は他の活性化関数を使うことが多いです。

勾配消失とは、微分値がゼロに近くなることです。シグモイドの場合は、値が大きく（小さく）なると勾配がゼロに近づきます。

最終段で、出力を0~1にするために使われることはありますね

x = torch.linspace(-5, 5, 100)
y = nn.Sigmoid()(x)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title("Sigmoid")
plt.grid()
plt.show()

グラフは、横軸が入力値（x）、縦軸が出力値（y）です。シグモイドの場合、大きな値（小さな値）は１（０）に近づく以下のようなグラフになります。

sigmoid

ハイパボリックタンジェント（Tanh）

入力を-1から1の範囲に変換します。シグモイド関数に似ていますが、出力範囲が-1から1と異なります。この関数も勾配消失の問題があります。

x = torch.linspace(-5, 5, 100)
y = nn.Tanh()(x)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title("tanh")
plt.grid()
plt.show()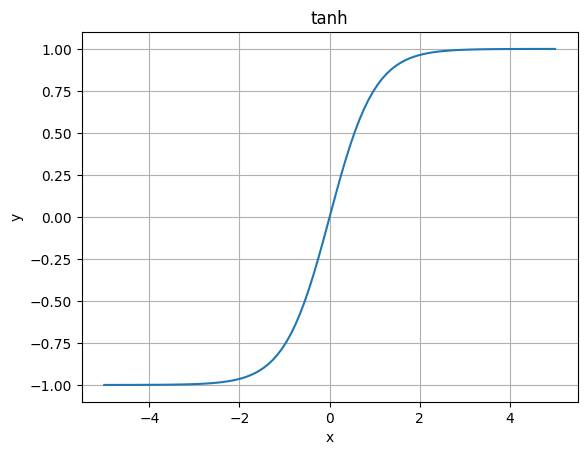
tanh

ReLU

2000年代に入り、ReLUが提案されました。計算効率が高く、勾配消失の問題を軽減できることが特徴で、ディープラーニング（深層学習）では最近もよく利用されています。

ReLUでは、入力がゼロより大きい場合はそのまま、ゼロ以下の場合はゼロとなる以下のような式になります。

$$
ReLU(x) = max(0, x)
$$

式から分かるように$$x=0$$が特異点となります。また、$$x < 0$$については勾配が常に0になるため、勾配消失の問題が発生する可能性があります。

x = torch.linspace(-5, 5, 100)
y = nn.ReLU()(x)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title("ReLU")
plt.grid()
plt.show()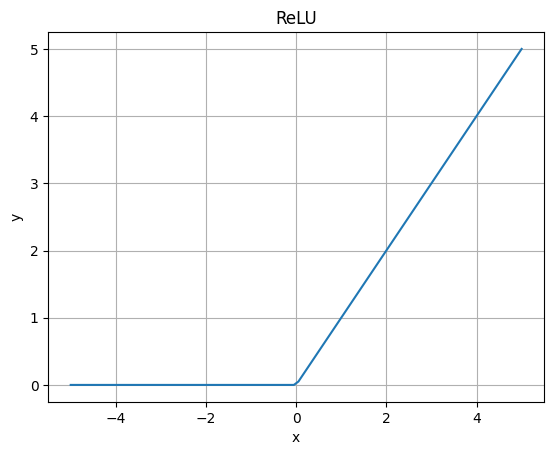
ReLU

LeakedReLU

ReLUの改良版で、ゼロ以下の領域で微小な傾きを持ちます。これにより、ゼロ以下の入力でも微小な勾配が伝播し、一部のタスクではReLUよりも優れた性能を発揮します。

x = torch.linspace(-5, 5, 100)
y = nn.LeakyReLU()(x)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title("LeakyReLU")
plt.grid()
plt.show()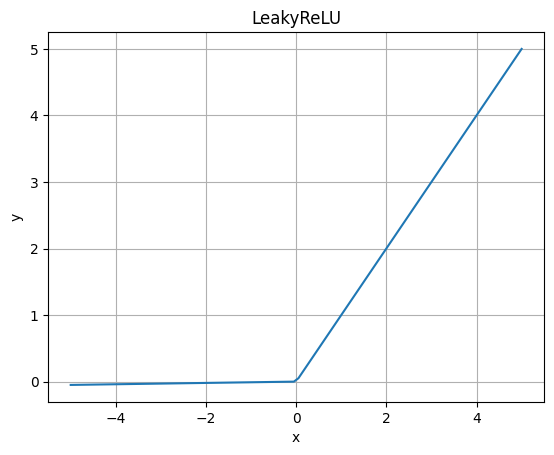
ReakyReLU

グラフではわかりにくいですが、０以下が僅かに傾斜しています

GELU

GELUは、GPTやBERT（Bidirectional Encoder Representations from Transformers）などの自然言語処理タスクで利用されている活性化関数です。

ReLUに比べて0付近で滑らかな形状を持ちます。

x = torch.linspace(-5, 5, 100)
y = nn.GELU()(x)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title("GELU")
plt.grid()
plt.show()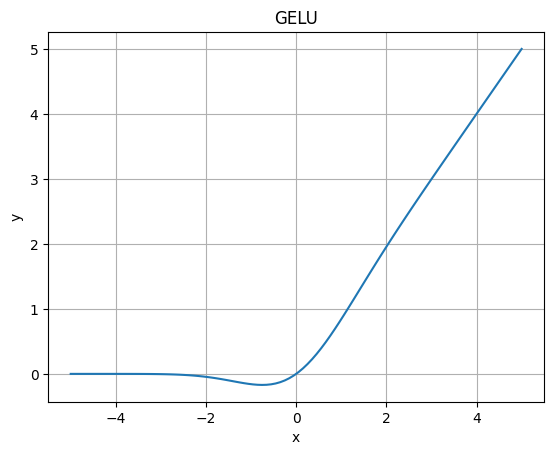
GELU

Mish

ReLUの改良版にSwishという活性化関数がありますが、Swishの改良版がMishになります。

ReLUやSwishよりもなめらかで、勾配消失の問題に対処することができるとされています。

x = torch.linspace(-5, 5, 100)
y = nn.Mish()(x)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title("Mish")
plt.grid()
plt.show()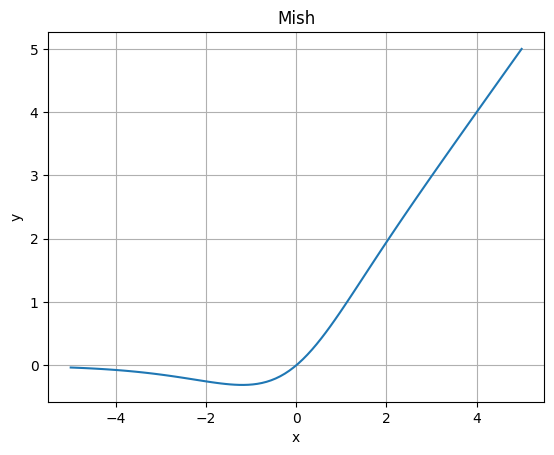
MISH

どの活性化関数が良いの？

計算効率が高いのはReLU

勾配消失の問題を緩和し、かつ、計算効率が高いのがReLUです。個人的には、とりあえず、ReLUで組んでみることも多いです。

タスクに応じて選ぶ

タスクによって適した活性化関数は違います。自然言語処理でGELUが使われていますし、他のタスクでは違った活性化関数の方がよいこともあります。

まずは、ターゲットとするタスクでよく使われている活性化関数を調べてみましょう。

結局、評価してみるしかない

結局、活性化関数を変えて評価実験するのが一番良いと思います。Pytorchの場合、活性化関数を変更するのは比較的簡単です。

ハイパーパラメーターの調整の１つとして、活性化関数の評価も行ってみるべきです。

まとめ

以上、活性化関数について簡単にまとめました。

初級 深層学習講座シリーズはこちら
もっと見る
ディープラーニングに関する記事一覧はこちら
ディープラーニング関連の記事一覧
ディープラーニング関連の記事一覧

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

ABOUT ME
ある/Aru
ある/Aru
IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)
Contact
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
おすすめ書籍
Recommend
こちらの記事もどうぞ
記事URLをコピーしました