MENU
プログラミング
記事内に商品プロモーションを含む場合があります

Python｜UnionFind（DSU）クラスの実装と利用方法

Aru

Union-Find（またはDisjoint Set Union, DSU）は、グループ管理を効率的に行うためのデータ構図です。グラフの処理や、クラスター分析などでよく利用されるデータ構造で、AtCoderなどの競技プログラミングの世界でも頻繁に利用されるデータ構造です。この記事では、PythonでUnionFindクラス（DSUクラス）を実装する方法と、使い方を解説します。

あわせて読みたい
AtCoderで役立つ記事一覧（Python, Go言語）
AtCoderで役立つ記事一覧（Python, Go言語）
Contents
  1. UnionFind（素集合データ構造）
  2. 応用例
  3. Pythonでの実装（クラス定義）
  4. 使い方
  5. 参考：Pythonのコード全体

UnionFind（素集合データ構造）

UnionFind（または、DSU, Disjoint Set Union）と呼ばれるデータ構造は、データの集合を素集合に分割して管理するデータ構造です（WikiPedia）。

このデータ構造を用いると、「ある要素XとYが同じ集合に含まれているか？」「要素Xと同じ集合に含まれている要素の個数」などを高速に求めることが可能です。

このデータ構造に対する基本操作は以下になります

  • merge(x, y)
    union(x,y),unite(x,y)などと書かれることもあります。xを含む集合と、yを含む集合を統合して１つの集合する処理です。merge(x, y)とmerge(y, z)を行うと、xとzは同じ集合に含まれるようになるのが特徴です。このように集合の結合を行うのがMergeです。
  • leader(X)
    find(X)と書くこともあります。Xを含む集合の代表の要素を返します。同じ集合に含まれる要素であれば、代表の要素の値は同じになります。グラフとして考えると、これは根（Root）になります。

また、これ以外に以下の操作を用意することもあります。

  • same(X, Y)
    要素X,Yが同じ集合に含まれているかどうかをtrue, falseで返します
  • size(X)
    要素Xが含まれる集合の要素数を返します。１の場合は、孤立していることになります。
  • groups()
    各グループに含まれる要素を列挙します

応用例

  • SNSでの友人グループの特定
    UnionFindは、友人関係を管理するのに便利です。「AさんとBさんが友達」「BさんとCさんが友達」といったたくさんの情報から、友達繋がりのあるグループを作成することができます。UnionFindを用いることで、AさんとZさんがつながっているか？などを高速に検索することが可能になります。
  • 距離に基づく点のグループ化
    距離が閾値以下の点だけを繋げた時に、到達できる点の集合を調べることができます。例えば、「中心(xi,yi)、半径ri」の円が沢山ある場合に、連結されている円をグループ化することができます。
  • 最小全域木（MST）
    UnionFindを使うと「最短コストで全てのノードを接続する辺の集合」を求めることができます。これを求めるには、辺を長さの短い順にソートしておき、辺で接続される２つの点がUnionFindの同じグループであれば、スキップ、同じグループでなければ辺を追加して２つの点をmergeします。これを繰り返すことでMSTを求めることができます。
  • データ分析・解析
    データ分析・解析でも、「AとBの直接の関係が記述されていない時に、２つが同じグループに含まれているか」というチェックは結構頻出です。

これらを高速に行うことができるUnion-Findは、知っておくと意外と実務でも重宝します。

個人的には、kaggleのコンペのデータ分析などに使うこと多いです。特に、Kaggleだと実行時間に制限があるので、検索処理を高速化できれば、その分他の解析処理ができるようになり有利です。

また、実務でも「知っていて良かった」というシチュエーションに何度か遭遇したのを覚えています。

Pythonでの実装（クラス定義）

UnionFindをPythonで実装します。今回はクラスとして実装することにします。

コード全体はここにあります。

実装ではUnionFindではなく、DSUとしています。AtCoderのライブラリに合わせた形です。

データ構造

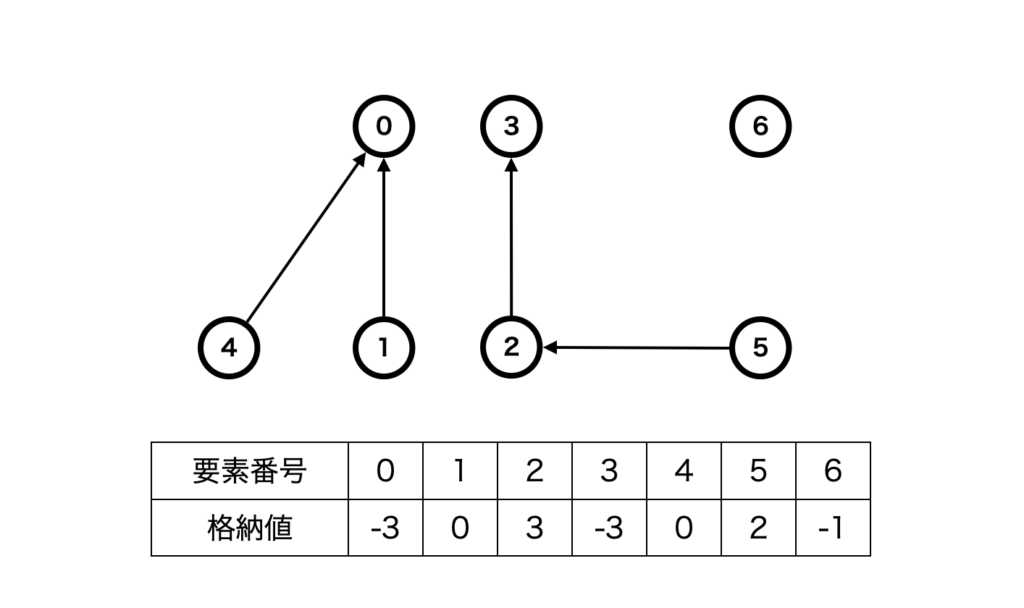
以下の図はデータ構造をグラフで表現したものです。

UnionFindのデータの実態はリストです。

例ではノードが7個あるので、サイズ７のリストなります。

管理する必要があるのは「親となる要素の番号」と「接続されているノード数」ですが、代表の要素（集合を代表するノード）に関しては「親となる要素の番号」は必要なく、また、それ以外のノードについては「接続されているノード数」を管理する必要がないので、代表ノードは要素数を、その他は親のノードを記録するようにすれば１つのリストで管理可能です。

このとき、要素数を負、親の要素の番号を正で表現することにすれば、要素数と要素番号を区別することができます。

下図では、要素0, 1, 4が同じ集合に、2, 3, 5が同じ集合に、そして6が単独の要素として示されています。集合の代表要素となる要素0, 3, 6には、それぞれの集合の要素数が格納されています（負数として）。他のノードは親のノードの要素番号が格納されています。

以下では、このような配列を生成するコードを実装します。

クラスの雛形を作成

まずクラスの雛形を作成します。__init__()は、初期化を行う関数です。また、その他は、上で説明した関数になります。

class DSU:
    def __init__(self, n) :
    
    def merge(self, a, b) :
    
    def same(self, a, b) :
    
    def leader(self, a) :
    
    def size(self, a) :

    def groups(self) :

初期化（__init__）

初期化では、要素数nを受け取って、配列を初期化します。

引数は、要素数nです。最初は、すべての要素は別々の集合なので、配列は-1に初期化しておきます。こうすることで、それぞれが１個だけの集合だと定義されます。

    def __init__(self, n) :
        self.n = n
        self.parentOrSize = [-1] * n

Leader

集合の代表要素の番号を返す関数です。

要素の値が負数になるまで再起的に呼び出せば、代表要素の番号を返すことができます。

    def leader(self, a) :
        if self.parentOrSize[a] < 0 :
            return a
        self.parentOrSize[a] = self.leader(self.parentOrSize[a])
        return self.parentOrSize[a]

Merge

集合aとbを結合する関数です。

それぞれの集合の代表（Leader）を調べて、片方を反対側の集合に繋げます。

これで全体が１つの集合となります。

サイズ比較してどちらを親にするか決める処理が入っていますが、これは、深さを小さくするためのテクニックです。

    def merge(self, a, b) :
        x, y = self.leader(a), self.leader(b)
        if x == y :
            return x
        if -self.parentOrSize[x] < -self.parentOrSize[y] :
            x, y = y, x
        self.parentOrSize[x] += self.parentOrSize[y]
        self.parentOrSize[y] = x
        return x

Same

要素aとbの代表要素（Leader）が同じかどうか調べて返すだけです。

    def same(self, a, b) :
        return self.leader(a) == self.leader(b)

Size

要素数を返すSizeもLeaderが実装できていれば簡単に実装することができます。

    def size(self, a) :
        return -self.parentOrSize[self.leader(a)]

Groups

グループをリスト化して返します。Leaderで親を調べて、親のリストに要素を加えていきます。前半部分はdict（辞書型）を使って、それぞれの要素がどの代表要素のグループに含まれるかを求めています。

最終的に、辞書をリストに変換してリストとして返しています。

    def groups(self) :
        m = {}
        for i in range(self.n) :
            x = self.leader(i)
            if x in m :
                m[x].append(i)
            else :
                m[x] = [i]
        return list(m.values())

使い方

以下のような使い方をします。

uf = DSU(要素数)という形で最初にインスタンスを生成します。

uf = DSU(10)
uf.merge(0, 1)
uf.merge(2, 3)
uf.merge(4, 5)
uf.merge(6, 7)
uf.merge(8, 9)
uf.merge(0, 3)
for e in range(10):
    print(uf.leader(e), uf.leader(e))
print(uf.same(0, 1))
print(uf.same(2, 3))
print(uf.same(4, 5))
print(uf.same(6, 7))
print(uf.same(8, 9))
print(uf.same(1, 9))
print(uf.groups())

出力結果

0 4
0 4
0 4
0 4
4 2
4 2
6 2
6 2
8 2
8 2
True
True
True
True
True
False
[[0, 1, 2, 3], [4, 5], [6, 7], [8, 9]]

UnionFindは結構簡単に実装できるのに、かなり便利なデータ構造です。実装の流れを含め覚えておくと良いです。

参考：Pythonのコード全体

以下に、コード全体をつけておきます。テンプレ的に使ってもらってもOKです。

#
# Disjoint Set Union: Union Find Tree
#
class DSU:
    def __init__(self, n) :
        self.n = n
        self.parentOrSize = [-1] * n
    
    def merge(self, a, b) :
        x, y = self.leader(a), self.leader(b)
        if x == y :
            return x
        if -self.parentOrSize[x] < -self.parentOrSize[y] :
            x, y = y, x
        self.parentOrSize[x] += self.parentOrSize[y]
        self.parentOrSize[y] = x
        return x
    
    def same(self, a, b) :
        return self.leader(a) == self.leader(b)
    
    def leader(self, a) :
        if self.parentOrSize[a] < 0 :
            return a
        self.parentOrSize[a] = self.leader(self.parentOrSize[a])
        return self.parentOrSize[a]
    
    def size(self, a) :
        return -self.parentOrSize[self.leader(a)]

    def groups(self) :
        m = {}
        for i in range(self.n) :
            x = self.leader(i)
            if x in m :
                m[x].append(i)
            else :
                m[x] = [i]
        return list(m.values())

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

ABOUT ME
ある/Aru
ある/Aru
IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)
Contact
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
Recommend
こちらの記事もどうぞ
記事URLをコピーしました