Python|最長増加部分列(LIS)を求める方法とその1つを再構成する方法

最長増加部分列(LIS)とは、与えられた数列の中で、増加順で取り出せる部分列の中で最の長いものを指します。この記事では、Pythonを使ってLISを効率よく求める方法と、LISの1つを再構成する方法について解説します。特に、再構成について扱っている記事は少ないと思いますので参考になればと思います
最長増加部分列(LIS)とは
最長増加部分列(Longest Increasing Subsequence, LIS)とは、数列$A_n$の部分列として作ることができる増加部分列の中で最も長い部分列のことです。
例えば、数列A=[3,1,4,2,5]の場合、長さ2以上の増加部分列として、[3,4],[3,5],[3,4,5],[1,4],[1,4,5],[1,2],[1,2,4],[4,5]などを作ることが可能です。この中で最も長いのは[3,4,5],[1,4,5],[1,2,5]で、最長増加部分列の長さは3となります。
この記事では、長さを求めるアルゴリズムを紹介し、また、最長部分列を1つ再構成する方法について紹介します。
最長増加部分列の長さを求める方法
以下が、最長増加部分列の長さを求めるプログラムになります。
import random
import bisect
def lis(a, inf = 1e18) :
n = len(a)
dp = [inf] * n
for i in range(n) :
pos = bisect.bisect_left(dp, a[i])
dp[pos] = a[i]
return bisect.bisect_left(dp, inf)
a = [random.randint(1, 10) for _ in range(5)]
print(a)
print(lis(a))
# 実行結果
# [5, 9, 5, 1, 9]
# 2このプログラムは動的計画法と二分探索法を組み合わせたものになります。dp[idx]という変数には、「i個目までの値を見た時に、idx番目に小さい変数の値」が格納されています。
A=[5,9,5,1,9]で考えてみます
最初dpは全て最大値で初期化されています([inf, inf, inf, inf, inf])。
まずA[0] = 5で考えると、これはdpの中で一番小さい値です。ですから、dp[0]の値を更新します。
[5, inf, inf, inf, inf]
次に、a[1] = 9だとこれはdpの中で5の次に小さい値になります。なので、5の隣を9に書き換えます。
[5, 9, inf, inf, inf]
次にa[2] = 5ですが、これは1番目の値と同じです。なので5を書き換えます(同じ値なので更新しても変化しません)
[5, 9, inf, inf, inf]
次にA[3] = 1で、これは5よりも小さくなります。ここでは、5が1に書き換えられます。
[1, 9, inf, inf, inf]
最後にA[4] = 9ですが、9はすでにありますので、9の場所が更新されます(変化しない)。
[1, 9, inf, inf, inf]
最終的に、infの手前に2の値が入っているので、最長部分増加列の長さは2となります。
なお、「それぞれの値が何番目に小さいか」を判定する処理には二分探索を用います。
このアルゴリズムでは、先頭からN回二分探索を行うので計算量はO(NlogN)となります。
上記の操作を図示したものが下図になります。図の方が理解しやすい方は以下の図も参考にしてみてください。
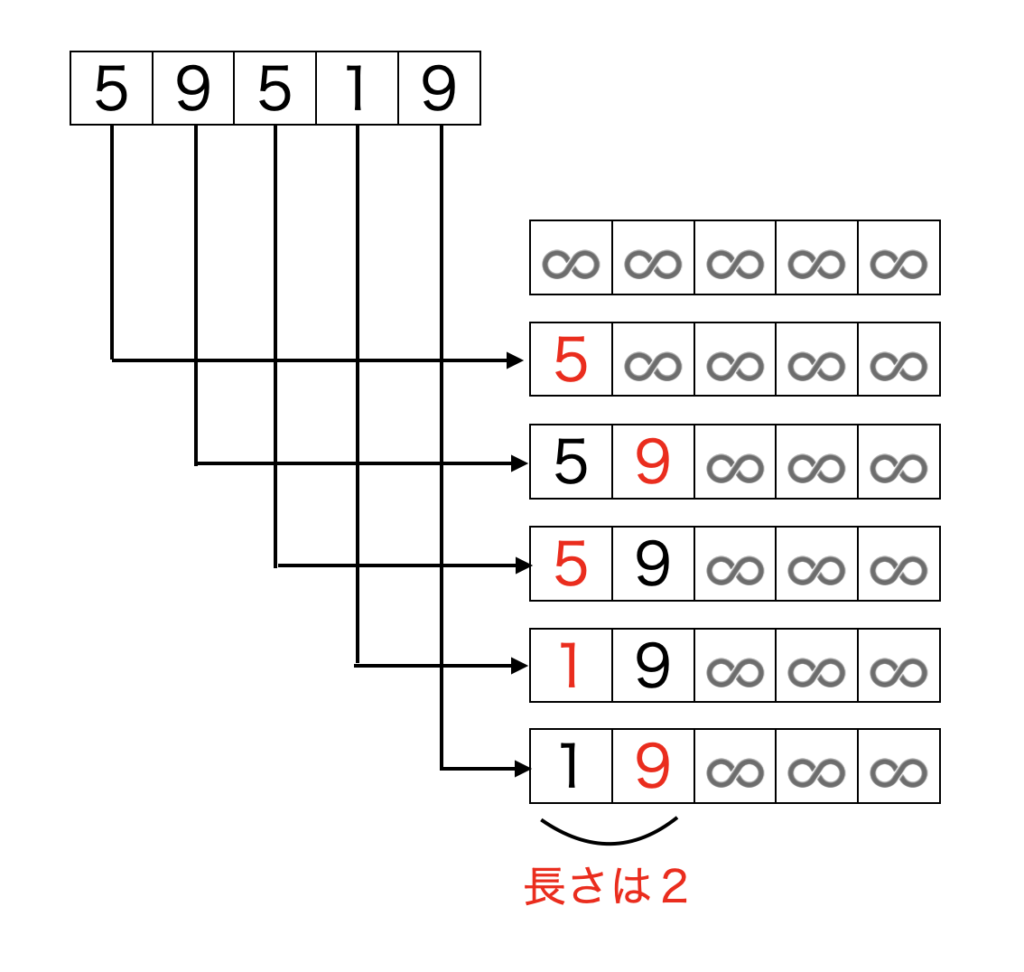
dp[idx]に記録されている値は、先頭からi番目までに現れた数値でidx番目に小さい値です。つまり、現在の位置iより手前に必ずdp配列に記録されている値がidx番目に存在することになります。なので、idx個の増加部分列を必ず作ることができます。
例えばdp=[1,4,5,7,inf,inf]の場合、a[i]=6であれば、i番目より手前に1,4,5の3つは確実に存在していることになります。なのでi番目まで6を使ってできる増加部分列は4になります。
最長増加部分列の1つを再構成する方法
上記のアルゴリズムで最長増加部分列の長さは求めることができます。ここでは、最長増加部分列の1つを構成してみたいと思います。
最初に説明したように、数列A=[3,1,4,2,5]の場合、最長増加部分列の長さは3で、[3,4,5],[1,4,5],[1,2,5]の3パターンが存在します。ここでは、この中の、どれか1つを再構成することを考えます。
再構成まで行うプログラムは以下になります。lis2()は、最長増加部分列の長さと、最長増加部分列の要素となる要素番号と、構成した最長増加部分列を返す関数になります。
import random
import bisect
def lis2(a, inf = 1e18) :
n = len(a)
dp = [inf] * n
l = []
for i in range(n) :
pos = bisect.bisect_left(dp, a[i])
dp[pos] = a[i]
l.append(pos+1)
ans = []
pos = []
cur = bisect.bisect_left(dp, inf)
for i in range(n-1, -1, -1) :
if l[i] == cur :
ans.append(a[i])
pos.append(i+1)
cur -= 1
return bisect.bisect_left(dp, inf), pos[::-1], ans[::-1]
a = [random.randint(1, 10) for _ in range(10)]
print(a)
n, p, v = lis2(a)
print(n)
print(*p)
print(*v)
# 実行結果
# [7, 9, 9, 7, 6, 10, 10, 8, 2, 1]
# 3
# 1 3 7
# 7 9 10処理としては先に説明したlis()と同じようにdp配列を使って最長増加部分列を計算します。ただ、動的計画法でdpを更新すると同時に、i番目の数値で作れる最大の長さをリストlに記憶する処理を追加しています。
lには、i番目の値で作れる最大の長さが記録されています。
cur=最長増加文字列の長さとして、cur==l[i]となる要素を末尾から調べていきます。最長増加文字列と同じ長さのl[i]が見つかったら、その位置をposに、値をansに記録します。あとは、curを1ずつ減算しながらcur==l[i]となる要素を見つけたら追加する処理を繰り返します。
例えば、長さが3の場合、3, 2, 1という数字をlの末尾から検索します。l[i]を逆順に辿って見つかったものが最長増加部分列のパターンの1つになります。
あとは、pos, ansを逆順にすれば、先頭からの要素番号と要素の値になります。
このように再構成することで、パターンの1つ出力することができます。
まとめ
Pythonで最長増加部分列の長さと、部分列の1つを再構成する方法を紹介しました。部分列の長さを求める処理は色々なブログで解説されていますが、再構成する方法について書かれたものは少ないと感じます。この記事では、LISの求め方だけでなく、LISの1つを構成する方法も追加して解説しました。この記事が参考になれば幸いです。






