画像処理の基本を解説（輪郭抽出などのフィルタ処理）｜Python

Aru

最近はOpenCVなど便利なツールがあり、自分で画像処理のコードを書くことが少なくなりました。また、画像処理もAI化が進み、基本的な画像処理を使うことも減った気がします。この記事では、基本的な画像処理について解説します

Contents

はじめに
輪郭抽出
- ソーベルフィルタ
- ラプラシアンフィルタ
ぼかしフィルタ
- ガウスフィルタ
フィルタ設計について
- Pythonを使ったフィルタ設計方法
終わりに

はじめに

デジタル画像処理は、画像を入力して操作・解析・変換するための基本的な技術です。AIが発達する前は、画像の品質向上や情報抽出に画像処理が行われていました。代表的な画像処理ライブラリはOpenCVで、このライブラリを使うことでフィルタ処理や、拡大縮小、トリミング、コーナー検出などの様々な処理を簡単に行うことができます。

この記事では、「フィルタ処理」に焦点を当てて解説します。OpenCVなどのライブラリを使えば簡単にできるため、その原理などを理解せずに使っている方も多いのではないでしょうか？

ただ、画像処理の基本ですので知っておいて損はありません。

この記事では、エッジ抽出と平滑か処理について、いくつかのアルゴリズムを紹介しつつ解説していきたいと思います。

輪郭抽出

ソーベルフィルタ

ソーベルフィルタは、画像の勾配（傾き）を計算して、エッジを抽出するためのフィルタです。抽出したエッジ成分を一定の強さで元の画像に加算するとエッジ部分が強調できるので、デジタル写真のエッジ強調や輪郭強調と言った処理に利用されることがあります。

ソーベルフィルタは、大きく水平方向（x軸）と垂直方向（y軸）の勾配を抽出するものがあり、以下のような係数のカーネル（フィルタ行列）が利用されます。

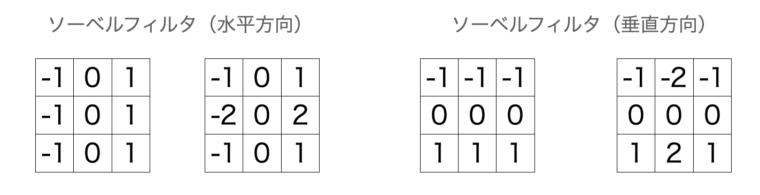
水平は横方向の勾配を、垂直は縦方向の勾配を検出するように係数が設定されていることがわかると思います。水平方向の２つ係数の違いは中央部分を重視するかどうかです。また、係数は全て足すとゼロになることもポイントです（エッジ抽出のフィルタでは、係数を足すとゼロになるように設計します）。今回は中央が-2, 2であるフィルタを利用してプログラムしてみます。

以下がPythondで作成したソーベルフィルタの例です。

プログラムでは、coreという変数がありますが、これはコアリングと呼ばれるもので、微小な勾配を除外する処理になります。これをいれておくと、小さな勾配を無視することができます。

import numpy as np
from PIL import Image

def apply_sobel_filter(image, dir = 0, core = 0):
    # ソーベルフィルタのカーネル
    sobel_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
    sobel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])

    def convolve2d(image, kernel):
        h, w = image.shape
        kh, kw = kernel.shape
        pad_h, pad_w = kh // 2, kw // 2
        padded_image = np.pad(image, ((pad_h, pad_h), (pad_w, pad_w)), mode='constant')
        result = np.zeros_like(image, dtype=np.float32)

        for i in range(h):
            for j in range(w):
                result[i, j] = np.sum(padded_image[i:i+kh, j:j+kw] * kernel)
        
        return np.where((-core <= result) & (result <= core), 0, result)

    gray_image = np.array(image.convert('L'))  # グレースケール変換
    if dir == 1:
        grad = convolve2d(gray_image, sobel_x)
    else :
        grad = convolve2d(gray_image, sobel_y)
    
    # 勾配の大きさ
    return (np.clip(grad, -128, 127) + 128).astype(np.uint8)

# 画像の読み込みとフィルタ適用
image = Image.open('sample.png')
result = apply_sobel_filter(image, dir=0, core = 2)
Image.fromarray(result).save('sobel_result.jpg')

実行すると以下のようになります。

入力画像

今回の入力画像は以下になります。

dir=0の結果（core=2）

dir=0の場合は、垂直方向のエッジが検出されます。縦方向にエッジがある部分が検出されていることがわかります。

dir=1の結果（core=2）

dir=1の場合は、水平方向にエッジがある部分が検出されます。

ラプラシアンフィルタ

ソーベルフィルタでは、水平と垂直方向の勾配を別々に検出していましたが、ラプラシアンフィルタを使えば、水平と垂直を同時に検出することができます。ソーベルは勾配を検出するフィルタで微分に相当するフィルタでしたが、ラプラシアンフィルタは二次微分を利用したフィルタになります。

横方向だけで考えた場合、元画像（A0, A1, A2）、元画像の微分、二次微分は以下のようになります。

ラプラシアンフィルタでは、これを水平、垂直双方向に行った結果がフィルタ係数となっています。

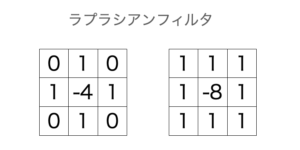
今回は、斜め方向のない左側のラプラシアンフィルタを使ってプログラムを作成してみました。プログラムは以下になります。こちらもcoreによりコアリングを行えるようにしています。

エッジ強調処理を行う場合は、ノイズ成分が強調されないようにコアリングを行うのが一般的です。この部分を工夫することで、より自然なエッジ強調を実現することが可能です。

import numpy as np
from PIL import Image

def apply_laplacian_filter(image, core=0):
    # ラプラシアンフィルタのカーネル
    laplacian_kernel = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]])

    def convolve2d(image, kernel):
        h, w = image.shape
        kh, kw = kernel.shape
        pad_h, pad_w = kh // 2, kw // 2
        padded_image = np.pad(image, ((pad_h, pad_h), (pad_w, pad_w)), mode='constant')
        result = np.zeros_like(image, dtype=np.float32)

        for i in range(h):
            for j in range(w):
                result[i, j] = np.sum(padded_image[i:i+kh, j:j+kw] * kernel)


        return np.where((-core <= result) & (result <= core), 0, result)

    gray_image = np.array(image.convert('L'))

    result = convolve2d(gray_image, laplacian_kernel)
    # import pdb; pdb.set_trace()
    return (np.clip(result, -128, 127) + 128).astype(np.uint8)

# 画像の読み込みとフィルタ適用
image = Image.open('sample.png')
result = apply_laplacian_filter(image, core=2)
Image.fromarray(result).save('laplacian_result.jpg')

結果画像（core=1）

core=1の画像です。

結果画像（core=2）

core=2の画像です。背景のボケた部分のエッジ成分が少なくなっていることがわかると思います。

ぼかしフィルタ

ガウスフィルタ

ガウスフィルタは、ガウス関数を使用して画像を平滑化するフィルタです。主にノイズ除去やぼかしに利用します。なお、元画像からガウスフィルタの結果を引くと、エッジ成分を抽出することができます。

ガウスフィルタでは、カーネルサイズ（平滑化を行うピクセルの範囲で奇数）と、ガウス関数の偏差（sigma）によりボケ量をコントロールします。sigmaを大きくする場合はカーネルサイズも大きくした方が良いです。

以下、ガウスフィルタのプログラムです。

import numpy as np
from PIL import Image

def apply_gaussian_filter(image, kernel_size=5, sigma=1.0):
    def gaussian_kernel(size, sigma):
        ax = np.arange(-size // 2 + 1, size // 2 + 1)
        xx, yy = np.meshgrid(ax, ax)
        kernel = np.exp(-(xx**2 + yy**2) / (2 * sigma**2))
        return kernel / kernel.sum()

    kernel = gaussian_kernel(kernel_size, sigma)

    def convolve2d(image, kernel):
        h, w = image.shape
        kh, kw = kernel.shape
        pad_h, pad_w = kh // 2, kw // 2
        padded_image = np.pad(image, ((pad_h, pad_h), (pad_w, pad_w)), mode='constant')
        result = np.zeros_like(image, dtype=np.float32)

        for i in range(h):
            for j in range(w):
                result[i, j] = np.sum(padded_image[i:i+kh, j:j+kw] * kernel)
        return result

    gray_image = np.array(image.convert('L'))
    result = convolve2d(gray_image, kernel)
    return np.clip(result, 0, 255).astype(np.uint8)

# 画像の読み込みとフィルタ適用
image = Image.open('sample.png')
result = apply_gaussian_filter(image, kernel_size = 7, sigma=1)
Image.fromarray(result).save('gaussian_result.jpg')