データの分布を正規分布に近づける（Box-Cox変換、Yeo-Johnson変換）|予測制度向上を目指して

多くの統計的手法や機械学習アルゴリズムでは、データが正規分布に従っていることを前提としています。ですから、データの分布が正規分布であれば、より正確な予測が可能となります。Box-Cox変換と、Yeo-Johnson変換は、データの分布を正規分布に近づけるための変換手法です。ここでは、この２つの手法について、Pythonで使う方法を含めて解説します。

データの前処理・特徴量エンジニアリングについては以下の記事にまとめています

機械学習で序盤に試す前処理と特徴量エンジニアリングの手法を解説【Python】

Box-Cox変換、Yeo-Johnson変換とは

Box-Cox変換とYeo-Johnson変換は、データの分布を正規分布に近づけるための変換方法です。

機械学習のアルゴリズムによっては、特徴量（データ）が正規分布に近い方がモデルの適合性が向上する場合があります。

例えば、線形回帰などは、特徴量（データ）が正規分布に従うことを前提としています。

「正規分布を期待するのであれば、データを変換して正規分布に従うように変換すればいい」ということで、正規分布に従うように変換するのがBox-Cox変換、Jeo-Johnson変換です。

Box-Cox変換の式は以下になります

$$
x\prime=\begin{cases}
\frac{x^\lambda – 1}{\lambda}& \text{if }\lambda\neq0,x\gt0\cr
\ln(x) &\text{if }\lambda=0,x\gt0
\end{cases}
$$

また、Yeo-Johnson変換は以下になります

$$
x\prime=\begin{cases}
\frac{(x+1)^\lambda – 1}{\lambda}& \text{if }\lambda\neq0,x\geq0\cr
-\frac{(x+1)^{2-\lambda} – 1}{2-\lambda}&\text{if }\lambda\neq2,x\lt0\cr
sign(x)\ln{(|x|+1)} &\text{otherwise}
\end{cases}
$$

定義を見るとわかるように、Box-Cox変換ではxが正でなければなりません。正負の値がある場合は、一旦正の値の範囲に＋αして動かすか、Yeo-Johnson変換を用いることになるかと思います。

私は、数式は一応確認しますが、どちらかというと使ってみて確認するタイプ

何に使う？

線形回帰のように正規分布を想定した手法で利用する場合は結構な効果がありそうですが、私個人としてはlightGBMやXGBoostなどの前処理でも使うことがあります。

変換自体は、sklearnに用意されていて比較的簡単に変換できるので、「とりあえず、試してみる」という軽い気持ちで使っても良いのではないかと思います。

精度向上のための１手法として、覚えておくことをお勧めします。

PyCaretの前処理としてもJeo-Johnson変換が用意されています。詳しくは以下の記事を参照してください

PyCaretの前処理（Preprocess）のまとめ｜欠損値の補完〜特徴量エンジニアリング

Pythonで変換を行う方法（sklearn）

sklearnに用意されているので、これを利用するのが手軽です。

Power Transformerをインポートします。

from sklearn.preprocessing import PowerTransformer

利用方法は以下のようになります。

Box-Cox変換

PowerTransformerにmethod='box-cox'を指定するとBox-Cox変換になります。

sel = 1
cols = df.columns
pt = PowerTransformer(method='box-cox')
pt.fit(df[cols].values)
df[cols] = pt.transform(df[cols].values)

Yeo-Johnson変換

PowerTransformerにmethod='yeo-johnson'を指定するとYeo-Johnson変換になります。

※デフォルトの変換はYeo-Johnsonなので、何も指定しない場合もYeo-Johnsonになります。

sel = 1
cols = df.columns
pt = PowerTransformer(method='yeo-johnson')
pt.fit(df[cols].values)
df[cols] = pt.transform(df[cols].values)

実験（実際に変換してみる）

ちゃんと変換されるかどうか、試してみます。

一様分布を変換

from sklearn.preprocessing import PowerTransformer
import numpy as np
import matplotlib.pyplot as plt

X = np.random.uniform(1, 100, 100000)
X = X[X > 2].reshape(-1,1)
plt.hist(X, bins=100)
pt = PowerTransformer(method='yeo-johnson')
pt.fit(X)
plt.show()
Y = pt.transform(X)
plt.hist(Y, bins=100)

データは10,000個。一様分布の乱数なので、ヒストグラムは下図のようになります。1から100までの値がほぼ同じ数存在していることがわかります。

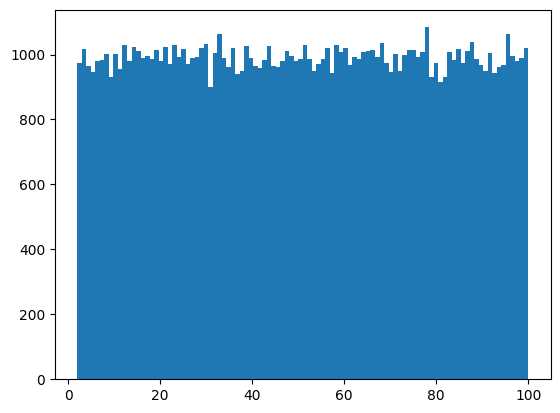
これをYeo-Johnson変換すると以下のようになります。

ヒストグラムが変化しましたが、正規分布？という感じです。一様分布に使うものではないと思うのですが、とりあえず分布が変化することは確認できました。

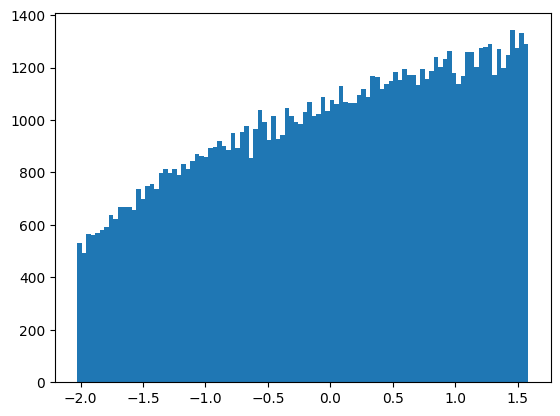
一応、変換後の平均と偏差を計算すると、

Y.mean(), Y.std()
(-1.875855790604598e-16, 1.0)

となるので、平均０、偏差１の分布には変換されているようです

ベータ分布を変換

次に、ベータ分布で生成した10,000個のデータに対して処理してみます。ベータ分布では、aとbを設定することで色々な確率密度関数を生成できますが、今回はa=2, b=10として、少し左寄りの分布を生成しました。

X = np.random.beta(2, 10, 100000)
X = X.reshape(-1,1)
plt.hist(X, bins=100)
pt = PowerTransformer(method='yeo-johnson')
pt.fit(X)
plt.show()
Y = pt.transform(X)
plt.hist(Y, bins=100)

プロットすると、以下のようになります。

なお、平均と分散は以下のようになります。

X.mean(), X.std()
(0.1666390210957959, 0.10307132826075942)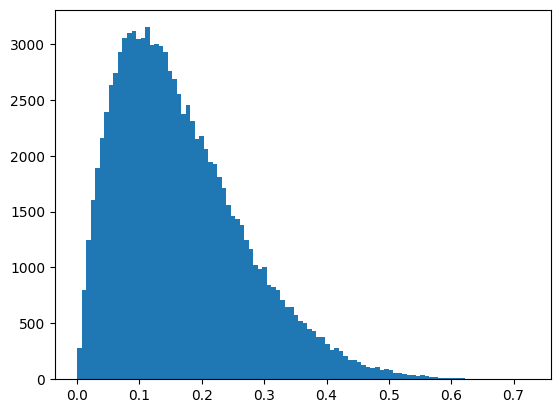

これをYeo-Johnson変換すると以下のようになります。今回は、正規分布っぽい分布に変化しました。

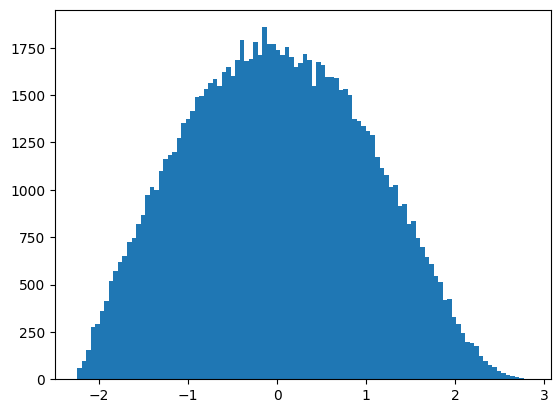
変換後の平均と分散は以下のようになり、平均０、分散１の正規分布に近づいていることがわかります。

Y.mean(), Y.std()
(3.5711877899302635e-16, 0.9999999999999998)

見た目でも正規分布に近づいたのがわかるので、今回作成した分布のようなものを正規分布に近づけるのには向いた変換のようです。

まとめ

Box-Cox変換、Yeo-Johnson変換について説明しました。データ分析、機械学習ではデータが正規分布であることを前提としたものが結構あるので、これらの変換を行うことで予測精度が向上することがあります。

精度向上の手法の１つとして覚えておいて損にならないと思います