Pythonで深さ優先探索（DFS）,幅優先探索（BFS）,ダイクストラ法を実装する
Aru
Aru's テクログ（Aruaru0）
A*アルゴリズムで効率良く最短経路を探索｜Pythonによる実装
Aru
最近、A*アルゴリズムを利用することが多くなりました。競プロなどでは使う機会は少ないですが、計算コストが問題となるシーンでは、ヒューリスティックを使って効率的に経路探索をするA*は結構有用です。ここでは、A*アルゴリズムの概要と、Pythonによる実装方法をBSFと比較しながら解説します。
A*アルゴリズム
A*アルゴリズムとは
経路探索問題を解く場合、深さ優先探索（DFS）や幅優先探索（BFS）がよく利用されます。最短経路探索の場合は、幅優先探索（BFS）やダイクストラ法などが利用されることも多いです。
これらの方法で探索を行なっても良いのですが、探索空間を効率的に絞り込み、計算コストを抑えながら最短経路を探索する手法としてA*アルゴリズムと呼ばれるアルゴリズムがあります。
A*アルゴリズムは、ヒューリスティック関数を利用して目標ノードへの推定コストを計算し、有望な経路を優先的に探索する手法です。
幅優先探索は探索途中の結果をキューに入れるためメモリを多く消費する傾向がありますが、A*アルゴリズムの場合はヒューリスティックを用いて優先する経路を決めるため、幅優先探索と比較してメモリ消費を抑えられる傾向にあります。
また、有望な方向から経路探索するため、経路探索時間も短くできる可能性があります。
ワーストケースでは、A*アルゴリズムの計算コストはBFSと同じとなりますが、適切なヒューリスティック関数を設計できる場合は通常はA*の方が効率が良いです。
この記事では、迷路探索に幅優先探索（BFS）と、A*アルゴリズムをPythonでコード作成し、両者の比較してみたいと思います。
実際にグラフ探索を使った事例はこちらの記事にあります。応用が気になった方はのぞいてみてください。
Santa 2023 : The Polytope Permutation Puzzleに挑戦| Kaggleチャレンジ記録
アルゴリズム概要
A*のアルゴリズムは以下の通りです。
- 初期化
- 探索：リストが空になるまで以下の手順を繰り返す
- コストf（f=g + h）が最小のノードを取り出す
- 取り出したノードがゴールであれば終了
- 取り出したノードから移動できるノードに対して
- 移動できるノードのgが更新（小さく）できる場合は、gを更新
- コストf=g+hを計算してリストに追加する
最小のノードを探索するため、ノードのリストは優先キューを用いて管理するのが一般的です。
コストfを計算するためのgとhは、それぞれ以下のようになります。
g：現在ノード（現在地点）までのコスト。既知ｈ：現在ノード（現在地点）からゴールまでのヒューリスティックコスト。推定値
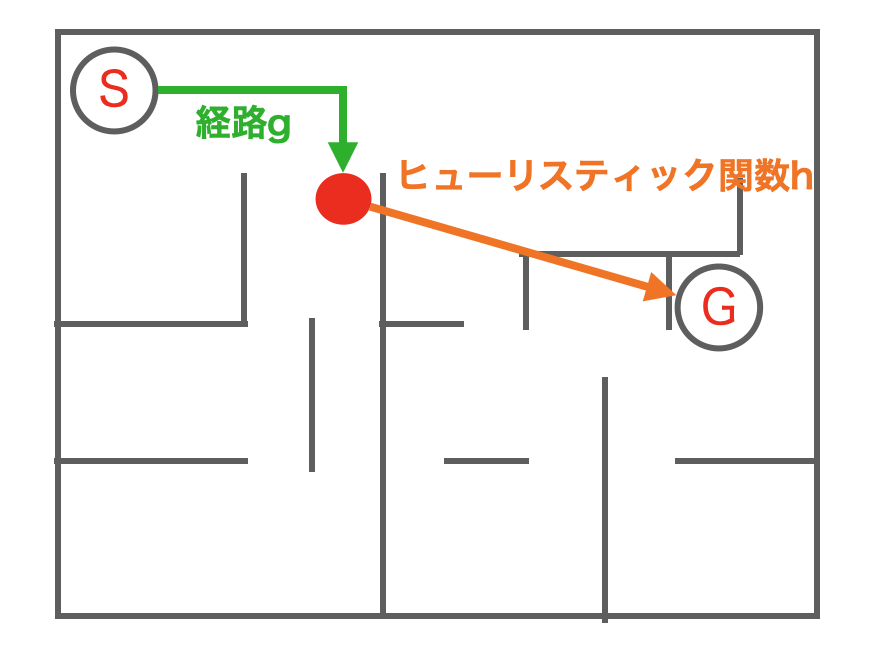
例えば、以下の図のような迷路の場合、gはスタート（S）から現在地点までに要した距離、hは現在位置からゴールまでの想定される距離になります。
hは独自に定義してよいです。例えば、下図のような迷路の場合は、ユークリッド距離やマンハッタン距離などを利用することもできます。
以下、実際にプログラムを作成しながら解説します。
今回、ターゲットとする迷路
今回ターゲットとする迷路は以下のものです。
最初の２つの値は高さ（H）と幅（W）です。
続くH行ｘW列は、迷路の形状を表す文字列です。文字#は壁、.は通路、SとGはそれぞれスタートとゴールになります。
9 22
######################
#S...................#
#....#...#........##.#
#....#...#...#######.#
######.#.###.#...#.G.#
#......#.#.....#.....#
######.#.#.###.#.#####
#........#.....#.....#
######################以下、上記のテキストを標準入力から受け取って迷路探索を行うものとします。
BFS（深さ優先探索で解く）
まず、BFSを使って経路探索してみます。
プログラムは以下のようになります。
H, W = map(int, input().split())
s = [input() for _ in range(H)]
sx, sy = 0,0
gx, gy = 0,0
for h in range(H):
for w in range(W):
if s[h][w] == "S" :
sx, sy = w, h
if s[h][w] == "G" :
gx, gy = w, h
for e in s : print(e)
print("start = ", sx, sy)
print("goal = ", gx, gy)
inf = 10**4
dist = [[inf for _ in range(W)] for _ in range(H)]
dist[sy][sx] = 0
dx = [-1,1,0,0]
dy = [0,0,-1,1]
def calc_dist(x0, y0, x1, y1) :
return abs(x0 - x1) + abs(y0 - y1)
cnt = 0
q = [(sx, sy)]
while len(q) != 0 :
cx, cy = q[0]
if cx == gx and cy == gy : break
q = q[1:]
for i in range(4) :
px, py = cx + dx[i], cy + dy[i]
if 0 > px or px >= W or 0 > py or py >= H : continue
if s[py][px] == "#" : continue
if dist[py][px] >= dist[cy][cx] + 1 :
dist[py][px] = dist[cy][cx] + 1
q.append((px,py))
cnt+=1
print("-"*80)
print(cnt, ":" , q)
for e in dist:
for v in e:
if v == 10000 : print(" *", end = " ")
else : print(f"{v:2}", end = " ")
print()
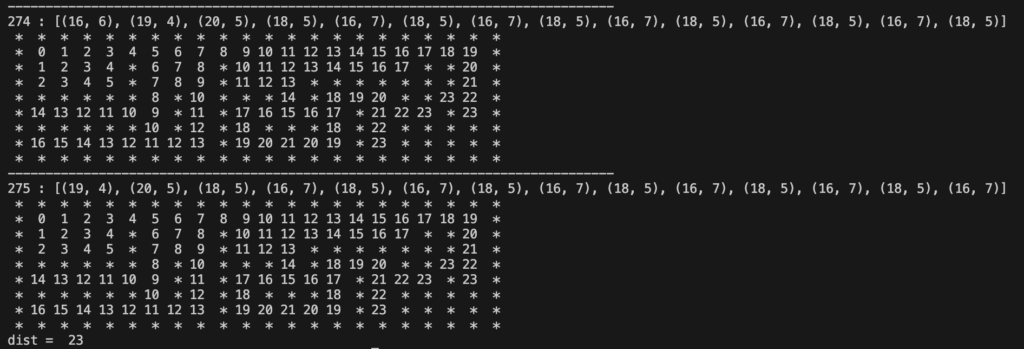
print("dist = ", dist[gy][gx])プログラムでは、途中経過がわかるようにdistの状態を表示しています。distは、スタートからの距離で現在地点の変化に合わせて更新されていきます。
実行結果は以下のようになります（末尾のみ）。これを見ると275ステップ目にゴールに到達していることがわかります。また、距離は23でした。
A*アルゴリズムで解く
次に、BFSのプログラムをA*アルゴリズムに修正します。以下が書き換えたプログラムになります。
import heapq
H, W = map(int, input().split())
s = [input() for _ in range(H)]
sx, sy = 0,0
gx, gy = 0,0
for h in range(H):
for w in range(W):
if s[h][w] == "S" :
sx, sy = w, h
if s[h][w] == "G" :
gx, gy = w, h
for e in s : print(e)
print("start = ", sx, sy)
print("goal = ", gx, gy)
inf = 10**4
dist = [[inf for _ in range(W)] for _ in range(H)]
dist[sy][sx] = 0
dx = [-1,1,0,0]
dy = [0,0,-1,1]
def h(x0, y0, x1, y1) :
return abs(x0 - x1) + abs(y0 - y1)
cnt = 0
pq = []
heapq.heappush(pq, (h(sx, sy, gx, gy), sx, sy))
while len(pq) != 0 :
d, cx, cy = pq[0]
heapq.heappop(pq)
if cx == gx and cy == gy : break
for i in range(4) :
px, py = cx + dx[i], cy + dy[i]
if 0 > px or px >= W or 0 > py or py >= H : continue
if s[py][px] == "#" : continue
if dist[py][px] >= dist[cy][cx] + 1 :
dist[py][px] = dist[cy][cx] + 1
heapq.heappush(pq, (dist[py][px]+h(px, py, gx, gy),px,py))
cnt+=1
print("-"*80)
print(cnt, ":", pq)
for e in dist:
for v in e:
if v == 10000 : print(" *", end = " ")
else : print(f"{v:2}", end = " ")
print()
print("dist = ", dist[gy][gx])
プログラム中のh()がヒューリスティック関数で、ここでは現在地点からのマンハッタン距離としました。
def h(x0, y0, x1, y1) :
return abs(x0 - x1) + abs(y0 - y1)プログラムを見てわかるようにBFSのプログラムをほぼ同じです。変化したのは、「キューで管理した部分」が「優先キュー」に置き換わったこと、優先キューの順番はf = g+hの小さい順となっていることです。
このように、ほんの少し書き換えるだけで、BSFからA*へ書き換えることが可能です。
A*のコードは、ダイクストラ法のコードに近いです。
Pythonで深さ優先探索（DFS）,幅優先探索（BFS）,ダイクストラ法を実装する
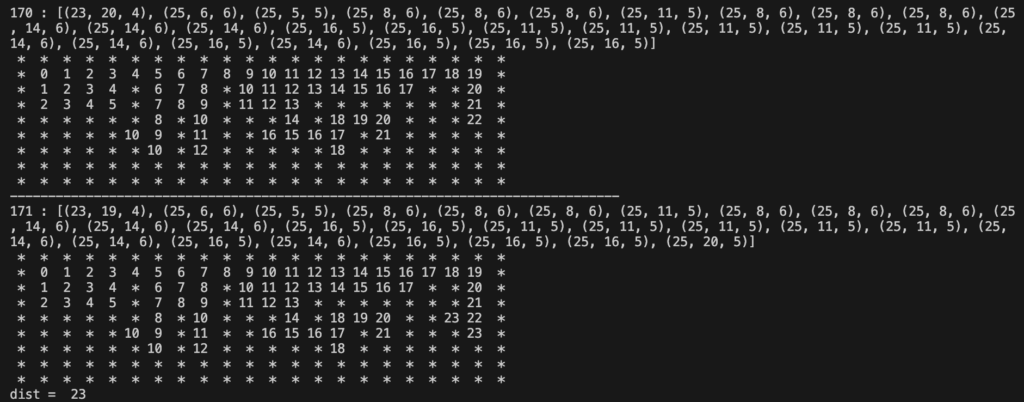
実行結果は以下のようになります。
目的地に近いものを優先して探索するので、171ステップ目にゴールに到達していることがわかります。また、距離は23とBFSと同じでした。BFSと比較すると100ステップ以上短いステップで経路を探索できていることがわかります。
以上のようにA*アルゴリズムを用いることで、経路探索を効率化できます。
ワーストケースではA*アルゴリズムが効率が良いとは言えませんが、多くのシーンでA*の方が効率が良いです。例えば、制限時間内に探索を完了させたい場合などに有効です。
まとめ
以上、A*アルゴリズムについて解説しました。制限時間内に経路を見つけたい場合などに効果的なので覚えておくと良いです。
ABOUT ME
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
