DeepSeek R1の蒸留モデルをローカルPCで試してみた(日本語対応)

Deepseek-R1が話題ですが、オープンソースとはいえかなり大きなモデル(3bit版でも300GBオーバー)なので、ローカルの環境ではとても動きません。Deepseek-R1の論文を見るとDeepseek-R1の蒸留モデルがあると書かれていたので、そちらを試して見ることにしました。この記事では、蒸留モデルのDeepSeek-R1-Distill-Qwen-32B-Japaneseを使ってみた結果について簡単に紹介します。
DeepSeek R1とは
DeepSeek R1は、DeepSeekの最新モデルです。ついこの間DeepSeek v3が出たばかりなのに開発スピードに驚かされます。
DeepSeek R1は、DeepSeek-v3をベースに、強化学習(RL)を適用することで推論性能を大幅に向上させたモデルです(厳密には、RLのみのDeepSeek-R1-Zeroと、教師あり学習とRLを組み合わせたDeepSeek-R1があるようです)。
オープンソースで公開されており、環境さえあればダンロードして自身のPCでも動作させることが可能なモデルです。
ただ、3bitに量子化されたモデルでも300GBオーバーなので、一般的なGPUを搭載した環境で動作させるのは厳しいです。
DeepSeek-R1-Distillとは
DeepSeek-R1-Distillは、蒸留というテクニックを使って、DeepSeek-R1を教師として学習させたモデルです。モデルには、Qwenベース(1.5B, 7B, 14B, 32B)と、Llama3.3ベース(8B, 70B)が用意されています。試しに、4bit量子化版のDeepSeek-R1-Distill-Llama-70Bを動かしてみたのですが、日本語の質問に対して中国語で返答することが多い印象です。
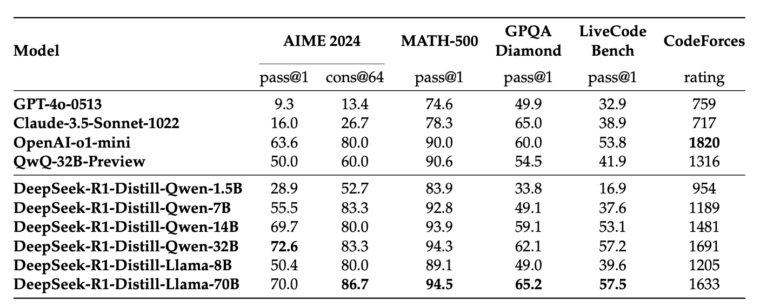
ちなみに、ベンチマーク結果は以下のようになっています。Qwen14Bより大きなモデルなら一部はOpenAI-o1-mini程度の結果を出しているようです。
DeepSeek-R1-Distill-Qwen-32B-Japaneseモデル
日本語のものがないか探したところ、Cyberagentが日本語でファインチューンしたモデルを出してくれています。ということで、このモデルを使って色々遊んでみました。
レビュー
利用環境
私が試した環境は、Macbook Pro(M4Max, 128GB)です。メモリを最大限に搭載したMacBookで、標準設定で96GBまでGPUに割り当てることができるので、比較的大きなLLMをどうさせることが可能です。
なお、今回はLM Studioを利用して実行を行いました。

速度は、nVIDIAのGPUにかないませんが、ある程度の速度で動くので動作させる目的ならMacbook Proは良い選択肢だと思っています。
DeepSeek-R1-Distill-Qwen-14B-Japaneseモデル
ダウンロードするとQ4_K_Mのモデルで8.99GBでした。10GB以下のモデルなので、16GBのモデルでも動作するかと思います。

MacBook Air(m2, 16GB)での動作も確認しました14Bであれば16GB搭載のMacBookでも動作するようです!
簡単なテスト
まずは、動作確認を兼ねた簡単なテストから。自分としては、おなじみの山の高さを聞くものです。これLLMは結構間違ったりするので面白いんですよね。
日本で一番高い山は?
DeepSeek R1の特徴は、このThinking…(Thoughts)という出力だと思います。これを見るとLLMがどのような過程で回答を考えたのかを知ることができます。
ユーザーからの質問は「日本で一番高い山は?」です。まず、この質問への回答を正確に提供する必要がありますが、単純に答えを述べるだけでなく、なぜその山が最高点であるのか説明することが重要です。
最初に思いつくのは富士山でしょう。しかし、地理の知識を確認する必要があります。日本における最高峰の山は富士山か、あるいは他の山々もあるかもしれません。例えば、立山や槍ヶ岳なども高い山として知られていますが、その標高はどれくらいなのでしょうか。
次に、正確なデータ源が必要です。信頼できる地理情報サイトや日本の公式機関(国土地理院)の情報を参照する必要があります。富士山の高度は約3776メートルとされていますが、これは実測値に基づくものでしょうか? あるいは、歴史的なデータとの違いがあるかもしれません。
また、海外からの観光客や学生向けに説明する場合、なぜ富士山が最高峰なのか理由を述べる必要があります。例えば、周囲の地形や火山活動による形成過程などです。さらに、文化的な側面として神聖な場所とされる点も触れると良いでしょう。
ユーザーが求めているのは表面的な答えだけでなく、その背景にある地理的・文化的な要素かもしれません。そのため、回答を深めることでより満足度の高い情報を提供できると考えられます。
ただし、誤った情報を伝えるリスクがあるため、正確なデータに基づく必要があります。例えば、過去に標高が変更されたケースや、測量方法の違いなどがあれば注意が必要です。国土地理院の公式サイトをチェックし、最新の情報と一致しているか確認します。
さらに、富士山以外にも高い山々があることを伝えることで、ユーザーの知識を広げることもできます。例えば、立山連峰や白馬岳などの高峠について触れると、日本の山域の多様性が伝わります。
最後に、回答の構成を考えます。まず問題を提示し、答えを述べた後にその理由を説明する形が適切でしょう。具体的な数値とデータソースを挙げることで信頼性が増します。
DeepSeek-Distillの思考の過程(?)です。勝手に「単純に答えを述べるだけでなく、なぜその山が最高点であるのか説明することが重要です」とか考えてるのが笑いました。
あと、富士山以外も例を出した方が良いとか、最高峰な理由を追加するとか色々考えています。こちらを読むと結構面白いです。
これを受けて、出てきた回答が以下になります。
日本で最高峰の山は富士山(標高3,776m)です。
富士山が最高峰である理由
- 地理的要因
- 周囲を高い山々が取り囲まず、独立した火山として突出している。
- 例:立山連峰(標高3,190m)や槍ヶ岳(2,567m)などより高い。
- 測量の根拠
国土地理院が2018年実施した航空機による高度測定で、頂上から約4mを含む3,776mと確定。これは歴史的な標高(例:3,742m)より高い。 - 文化的・地理学的背景
- 神聖な山として古来から崇拝され、現在も登山や信仰活動が継承。
- 火山活動の歴史と地質構造が独自性を生む。
補足情報
- 富士山の頂点:「富士宮駅」が基準点で測定され、頂上から約4m下に位置する。
- 海外からの視点:日本本土最高峰という点で東洋三十六名峰の一つとされる。
正確な情報は地理的な観点と文化的価値を結びつけたものであり、公式データに基づいています。
赤文字の部分は、正確性が怪しい部分です。他のLLMと同様に標高などの数値は苦手なようです。富士山の標高は正しかったですが、他の山の高さはめちゃくちゃです。また、富士宮駅は、さすがに富士山の頂上にはないと思います(笑)。
「日本で一番高い山は?」という質問は、いつも聞いてみている質問ですが、それぞれのLLMで結構違う回答があって面白いです。
プログラミング問題を解いてもらう
AtCoder ABC390のB問題を解いてもらいました。今回は、問題を手動でmarkdownに変換して入力しました。なお、システムプロンプトとして以下も加えています。
これから解いてもらう問題は、AtCoderのABCの問題の1つです。
AtCoderの問題は以下のような特徴があります。
AtCoderの問題の特徴
- A問題からF問題と難易度が上昇する
- 演算量が問題になることが多い。例えば、N^2で解ける問題だがNで解かないと間に合わないなど
- 問題には制約が与えられるのでそれを見て演算量を考え、適切な解放を選ぶ必要がある
- 二分探索、動的計画法、グラフなどをつかうことで解ける問題も多い
- 数学的な問題が出題されることもある
ここでは、以下の手順で解き、最終的にプログラムを作成してください。
- 問題の理解:問題を読み、まとめた内容を書く
- 方針の整理:どのようなアプローチで解くかを書く
- 解法:解法とそれに沿ったプログラムを書く
なお以下の情報が与えられます。
与えられる情報
- 問題文:問題文です
- 制約:制約です
- 入力フォーマット
- 入力例と出力例:入力と出力例です
B – Geometric Sequence / 実行時間制限: 2 sec / メモリ制限: 1024 MB
配点
200 点
問題文
長さ
N の正整数列 A=(A 1 ,A2 ,…,AN) が与えられます。
A が等比数列であるか判定してください。
制約
2≤N≤100
1≤A i ≤10^9
入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N
A 1 A 2 … AN
出力
A が 等比数列ならば Yes を、そうでないならば No を出力せよ。
以下、過程です。今回も少し考えています。
まず、問題を理解します。与えられた整数列が等比数列かどうかを判定する必要があります。等比数列の定義は、各要素が前の要素に一定の公比rで掛け合わされていることです。つまり、A[i+1]/A[i] = r(i=0から)がすべて成立しているか確認します。
次に制約条件を考えます。Nは2以上100以下なので、時間的な計算量には余裕があります。各要素を比較すれば良いのでO(N)の計算で十分です。
方針としては、公比rを最初の二項から計算し、その後すべての隣接する二項が同じ比率になるかチェックします。ただし、ゼロや割り切れない場合に注意が必要です。例えば、A[0]がゼロの場合、次の要素も全てゼロでなければなりません。また、各要素の比を浮動小数点で計算すると誤差が出る可能性があるので、整数同士での比較方法を考える必要があります。
具体的な手順:
- 配列の最初2つの要素から公比rを算出する。
- A[0]が0の場合、すべての要素が0であることを確認。もし途中で非零があればNo。
- そうでない場合は、A[1]/A[0]が整数かどうかチェック。例えば、5と3なら割り切れないため公比は存在しない(等比数列ではない)。
- 算出されたrを用いて、各隣接要素の比を確認する。
- 各iに対して、A[i+1] == A[i] * r を確認。ただし、整数同士の掛け算で計算することで誤差を回避できる。
- 全ての条件が満たされればYes、そうでなければNo。
例外ケースとして、全てゼロの場合も等比数列です(rは任意)が、最初に0がある場合、すべての要素が0であることを確認する必要があります。例えば、N=2でA=[0,5]なら公比は5/0となり無効なのでNoと判定します。
また、A[0]が1で次の要素が2の場合、r=2。次に4、8などであればYesです。もし途中で掛算結果と一致しなければNoになります。
このアルゴリズムを実装する際の注意点:
- 分母がゼロになる場合の処理(A[0] == 0の場合)
- 整数割り算による誤差回避
- 全要素が0である場合の判定
これらのケースを網羅したテストを行い、正しく動作することを確認します。
考え方自体は良いのですが、「A[i+1] == A[i] * r を確認」となっており、浮動小数点の計算が残っています。
出力された回答がこちらです。
問題の理解
与えられた整数列が等比数列(公比rで各要素が前の要素に掛け合わされる)かどうかを判定する問題です。等比数列の定義に基づき、すべての隣接要素間の比率が一致しているか確認します。
方針
- 公比rを最初の2つの要素から計算(A[1]/A[0])。
- A[0]が0の場合:全要素が0でなければNo。
- 割り切れない場合(例:3と5)は直接判定できないため、各隣接要素の積を比較します(公比r = a_{i+1} / a_i となるべきなので、a_{i} * r = a_{i+1} → a_{i+1} = a_{i} * (a_{i+1}/a_i) と計算)。
- 各要素の積を比較することで浮動小数点誤差を回避しつつチェックします。
解法
n, *rest = map(int, open(0).read().split())
a = rest[:n]
r = None
if a[0] == 0:
for num in a:
if num != 0:
print("No")
exit()
print("Yes")
else:
# 公比を計算
r = a[1] / a[0]
# 整数割り算で比較するため、掛け算して比較
for i in range(1, n-1):
if a[i+1] != a[i] * r:
print("No")
exit()
print("Yes")
# 初期値のrが未設定の場合(n=2で全要素0)
if r is None and all(x == 0 for x in a):
print("Yes")
else:
# 全てのケースを網羅していない場合
pass解説
- ゼロチェック: 最初の要素が0の場合、すべての要素が0でなければNo。
- 公比計算: 初期2要素から公比rを算出し(浮動小数点)、各隣接要素間で積比較を行うことで誤差を回避。
- 全要素チェック: 各要素に対して積が一致するか確認し、不一致があれば即時Noを出力。
この方法により、大規模なNに対しても効率的に判定できます。
上記のプログラム、提出するとWAになります。理由は赤文字の部分の計算の浮動小数点誤差です。ということで、一発でACすることができませんでした。浮動小数のケアはしてくれなかったようです(ちなみに、大きなモデルでは一発正解しました)

追加で「浮動小数点を使わないようにしてください。」と指示することでACできましたが、$a[i-1]*a[i+1] = a[i]^2$を利用するもので想定していた解法とは少し違って驚きました。
感想
ChatGPTも上位レベルのモデルで似たような出力がありますが、Thinking…の部分が楽しいです。ちなみに、論文を読む限りThinkingを出力すると、スコアが高くなるような強化学習を行なっているようです。
他にも少し使ってみましたが、質問ではなく、普通に会話するのが少し不得意な感じがしました。単に会話をするだけならCommand R+の方が良い感じです。
ローカルで動かすLLMは、やはり目的により使い分けするのが良さそうです。

Llama3.3 70Bベースの性能が高いみたいなのでそちらを使いたいですが、日本語で使う場合は英語・中国語混じりになりがちなので少し悩ましいです。
まとめ
以上、DeepSeek R1の蒸留モデルを動かしてみました。実際に使って見ると、オリジナルのQwenより賢い気がします。また、thinking…が出力されるのも過程が見れていい感じです。ローカルのLLMで、問題を解くには良い選択肢だと感じました。