2024.06.02 2024.08.29

記事内に商品プロモーションを含む場合があります

数列問題：差の総和や区間最大和の解き方まとめ｜Python

Aru

この記事では、数列計算のテクニックとして、数列$A_1, A_2, A_3, … , A_n$の$A_i – A_j$の総和、差の絶対値（$|A_i – A_j|$）の総和、区間最大和を求める方法について解説します。この手の数列問題はAtCoderのBeginner Contestなどで結構出題されます。愚直なアプローチでは制限時間内に間に合わないことが多いので、高速化が求められます。高速化のテクニックにはパターンがありますので、慣れておきましょう

Contents

パターン１：Ai – Ajの総和を求める問題
パターン２：|Ai – Aj|を求める（差の絶対値）問題
パターン３：積の総和（ΣΣAi×Aj）
- 解法
パターン４：区間和の最大値を求める
- 解法
- プログラム
まとめ

パターン１：Ai – Ajの総和を求める問題

数列の２つの要素の差の総和を計算する問題です。和の総和であれば簡単ですが、差の場合は順番によって正負が逆転するので少し考える必要があります。

問題

$A_1, A_2, … , A_n$という数列が与えられた場合に、以下の値を求めなさい

$$
\sum_{i=1}^{N} \sum_{j = i+1}^{N} (A_i – A_j)
$$

愚直解

愚直解は式通りの処理を実際に行うもので、以下になります。

このコードでは、iを0~N-1まで、jをi+1~N-1までループさせてa[i]-a[j]を計算し、結果に加算しています。

２重にループを行うので、計算量は（$O(N^2)$）になります。

n = 5
a = [5, 2, 4, 6, 1]

ans = 0
for i in range(n):
    for j in range(i+1, n):
        ans += a[i] - a[j]
    
print(ans)

高速化

５つの値をa,b,c,d,eとして考えてみます。すると、$A_i – A_j$の計算を列挙すると以下のようになります。

$$\begin{eqnarray}
a-b,\ &a-c,\ &a-d,\ &a-e\\
&b-c,\ &b-d,\ &b-e\\
&&c-d,\ &c-e\\
&&&d-e\\
\end{eqnarray}$$

行にi, 列にjをとって整理したのが下図（右）です。

行で見るとaは4回、bは3回、cは2回、dは1回出現していることがわかります。また、列で見ると-bが1回、-cが2回、-dが3回、-eが4回出現していることがわかります。

これを整理すると、下図９（左）になります。

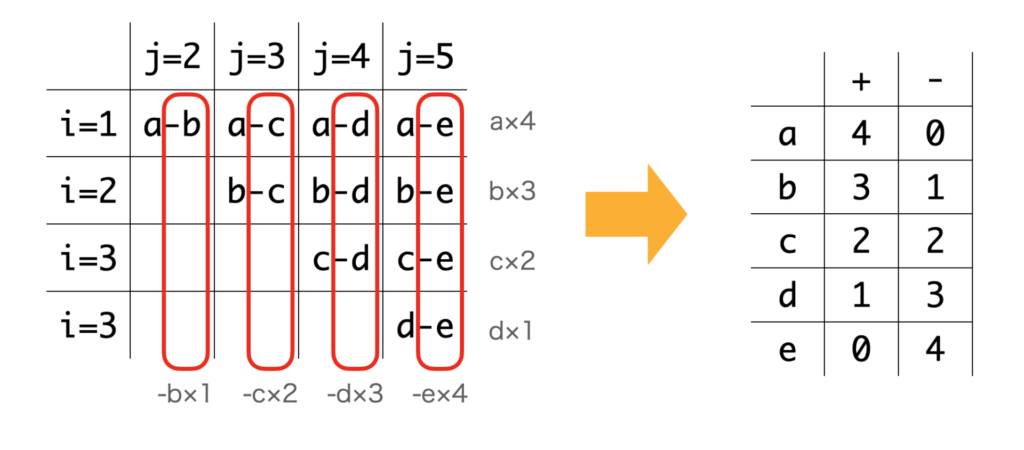
つまり、aはn-1回加算して0回減算、bはn-1-1回加算して1回減算することがわかります。

これをプログラムにすると以下のようになります。インデックスiは0スタートなことに注意してください。

２重ループ（$O(N^2)$）が$O(N)$となり高速化できました。

こんな感じで数式にして整理してみると、高速な解法がみつかったりします。

n = 5
a = [5, 2, 4, 6, 1]

print(a)

ans = 0
for i in range(n) :
    ans += a[i] * ((n-1-i) - i)

print(ans)

ランダムな数列で検算

実際に正しいかをランダムな値を10回生成して、愚直解と比較してチェックしてみます。

以下のプログラムは、愚直解と異なればNGを表示します。

import random

for _ in range(10) :
    n = random.randint(10, 100)
    a = [random.randint(1,100) for _ in range(n)]
    print("-"*100)
    print(len(a), a)

    ans1 = 0
    for i in range(n):
        for j in range(i+1, n):
            ans1 += a[i] - a[j]
        

    ans2 = 0
    for i in range(n) :
        ans2 += a[i] * ((n-1-i) - i)

    if ans1 == ans2 : print("OK")
    else: print("NG")

実行してみると以下のように全てOKになります。

----------------------------------------------------------------------------------------------------
24 [46, 74, 11, 2, 53, 87, 54, 2, 13, 19, 67, 61, 84, 87, 11, 64, 6, 68, 88, 28, 42, 44, 51, 53]
OK
----------------------------------------------------------------------------------------------------
15 [81, 72, 6, 63, 80, 67, 81, 84, 54, 57, 48, 3, 86, 1, 57]
OK
----------------------------------------------------------------------------------------------------
25 [69, 81, 26, 65, 43, 69, 86, 32, 73, 65, 60, 34, 19, 61, 21, 49, 78, 24, 57, 80, 95, 51, 80, 17, 33]
OK
----------------------------------------------------------------------------------------------------
50 [78, 37, 65, 65, 20, 30, 76, 16, 81, 23, 6, 91, 50, 41, 57, 10, 74, 86, 74, 2, 13, 88, 85, 13, 46, 15, 16, 9, 2, 69, 40, 77, 38, 75, 44, 81, 44, 48, 95, 32, 86, 9, 76, 34, 97, 77, 87, 81, 79, 78]
OK
----------------------------------------------------------------------------------------------------
83 [64, 91, 20, 20, 59, 25, 16, 2, 25, 93, 28, 19, 81, 41, 5, 75, 81, 87, 8, 21, 75, 91, 68, 38, 42, 16, 31, 39, 31, 31, 79, 90, 22, 29, 54, 74, 68, 99, 40, 23, 20, 89, 28, 57, 64, 61, 68, 91, 4, 59, 10, 31, 57, 6, 33, 43, 15, 92, 67, 47, 78, 26, 86, 55, 16, 18, 36, 48, 49, 9, 59, 59, 80, 4, 96, 90, 84, 66, 67, 18, 23, 97, 17]
OK
----------------------------------------------------------------------------------------------------
42 [89, 17, 78, 32, 10, 7, 11, 60, 1, 46, 52, 3, 76, 94, 12, 33, 87, 86, 74, 83, 30, 46, 21, 64, 91, 95, 96, 76, 52, 71, 93, 87, 100, 74, 1, 24, 8, 32, 97, 75, 71, 13]
OK
----------------------------------------------------------------------------------------------------
59 [27, 6, 95, 84, 39, 2, 61, 87, 75, 58, 84, 90, 22, 93, 78, 85, 79, 88, 78, 31, 63, 44, 3, 25, 44, 2, 31, 65, 43, 1, 100, 66, 48, 2, 92, 40, 23, 69, 8, 64, 13, 41, 1, 52, 26, 4, 4, 13, 17, 32, 86, 82, 33, 13, 98, 56, 36, 75, 18]
OK
----------------------------------------------------------------------------------------------------
36 [26, 70, 100, 17, 62, 46, 13, 61, 59, 50, 58, 4, 96, 41, 46, 35, 83, 91, 39, 5, 99, 9, 72, 79, 24, 10, 77, 86, 86, 66, 43, 55, 23, 85, 88, 40]
OK
----------------------------------------------------------------------------------------------------
30 [11, 19, 77, 44, 46, 93, 37, 34, 41, 22, 79, 72, 68, 97, 31, 39, 28, 18, 83, 77, 79, 43, 34, 75, 87, 97, 67, 12, 56, 49]
OK
----------------------------------------------------------------------------------------------------
36 [65, 54, 96, 56, 68, 23, 90, 93, 3, 80, 100, 16, 10, 48, 11, 95, 10, 77, 34, 30, 64, 86, 100, 28, 49, 93, 64, 71, 86, 63, 49, 100, 72, 40, 29, 36]
OK

パターン２：|Ai – Aj|を求める（差の絶対値）問題

先ほどの問題の解法と似たアプローチで解くことが可能です。

問題

$A_1, A_2, … , A_n$という数列が与えられた場合に、以下の値を求めなさい

$$
\sum_{i=1}^{N} \sum_{j = i+1}^{N} |A_i – A_j|
$$

愚直解

愚直回は、先ほどと同じでabs(a[i] - a[j])を求めるものになります。

n = 5
a = [5, 2, 4, 6, 1]

ans = 0
for i in range(n):
    for j in range(i+1, n):
        ans += abs(a[i] - a[j])
    
print(ans)

高速化

高速化の仕方は同じです。異なるのは、配列aをあらかじめ降順にソートしている点です。

ソートすることで、a[i]-a[j]が必ず正になるようにすることができます。a[i]-a[j]が正であれば絶対値の処理は必要ありません。

このように、ソートすることで簡単化できる場合があります。


n = 5
a = [5, 2, 4, 6, 1]

a.sort(reverse=True)

ans = 0
for i in range(n) :
    ans += a[i] * ((n-1-i) - i)

print(ans)

ランダムな数列で検算

実際に正しいかをランダムな値を10回生成して、愚直解と比較してチェックしてみます。

以下のプログラムは、愚直解と異なればNGを表示します。

本当にソートしても良いかも確認するために、愚直回を計算した後にsortしている点に注意してください。

import random

for _ in range(10) :
    n = random.randint(10, 100)
    a = [random.randint(1,100) for _ in range(n)]
    print("-"*100)
    print(len(a), a)

    ans1 = 0
    for i in range(n):
        for j in range(i+1, n):
            ans1 += abs(a[i] - a[j])
        

    a.sort(reverse=True)
    ans2 = 0
    for i in range(n) :
        ans2 += a[i] * ((n-1-i) - i)

    if ans1 == ans2 : print("OK")
    else: print("NG")

こちらも問題なく全てOKになりました。

----------------------------------------------------------------------------------------------------
50 [47, 33, 63, 7, 66, 94, 92, 1, 57, 80, 22, 22, 71, 41, 55, 13, 10, 74, 15, 34, 79, 54, 78, 52, 23, 76, 79, 54, 40, 61, 3, 89, 8, 86, 73, 91, 66, 78, 39, 7, 85, 48, 72, 62, 29, 21, 89, 69, 10, 33]
OK
----------------------------------------------------------------------------------------------------
67 [13, 5, 61, 76, 100, 40, 55, 77, 34, 4, 1, 72, 28, 41, 79, 83, 56, 98, 74, 58, 72, 77, 57, 24, 68, 57, 84, 57, 76, 2, 23, 53, 83, 21, 5, 17, 98, 8, 80, 23, 82, 59, 65, 67, 6, 57, 16, 80, 80, 9, 19, 94, 28, 54, 47, 46, 17, 100, 13, 17, 74, 38, 43, 69, 26, 33, 92]
OK
----------------------------------------------------------------------------------------------------
69 [76, 92, 84, 52, 35, 75, 42, 47, 9, 89, 45, 93, 56, 99, 11, 10, 96, 13, 16, 47, 40, 57, 22, 72, 3, 70, 32, 21, 16, 77, 7, 60, 24, 20, 50, 55, 39, 65, 62, 77, 55, 41, 97, 61, 59, 59, 40, 99, 25, 37, 19, 65, 4, 99, 64, 13, 43, 52, 21, 9, 47, 43, 32, 81, 51, 55, 42, 39, 90]
OK
----------------------------------------------------------------------------------------------------
48 [37, 9, 22, 6, 99, 77, 23, 57, 15, 26, 51, 88, 32, 77, 12, 30, 27, 66, 20, 30, 63, 11, 8, 93, 54, 87, 78, 54, 79, 81, 46, 26, 21, 12, 90, 72, 1, 88, 61, 27, 72, 75, 50, 48, 64, 36, 24, 36]
OK
----------------------------------------------------------------------------------------------------
55 [28, 33, 2, 1, 43, 45, 77, 90, 92, 6, 39, 21, 4, 9, 82, 82, 26, 60, 71, 83, 65, 98, 55, 18, 88, 39, 61, 73, 78, 2, 44, 80, 27, 24, 26, 84, 30, 24, 33, 100, 23, 80, 73, 41, 96, 61, 27, 65, 27, 93, 33, 1, 24, 21, 22]
OK
----------------------------------------------------------------------------------------------------
76 [21, 48, 8, 48, 65, 27, 18, 41, 76, 57, 85, 29, 69, 20, 14, 15, 29, 75, 5, 70, 31, 74, 3, 14, 24, 17, 43, 49, 25, 88, 60, 57, 25, 70, 90, 96, 25, 56, 9, 36, 46, 35, 35, 10, 31, 97, 53, 92, 43, 37, 13, 36, 11, 1, 18, 44, 35, 4, 84, 21, 43, 32, 31, 81, 1, 76, 28, 18, 80, 13, 68, 74, 15, 87, 10, 79]
OK
----------------------------------------------------------------------------------------------------
94 [92, 68, 85, 99, 70, 29, 99, 89, 22, 88, 46, 15, 66, 31, 63, 35, 88, 24, 98, 72, 12, 20, 17, 80, 61, 55, 43, 26, 31, 39, 73, 43, 56, 55, 97, 2, 69, 20, 74, 71, 84, 10, 30, 1, 16, 100, 22, 65, 1, 28, 54, 3, 33, 71, 94, 82, 59, 72, 52, 42, 56, 48, 64, 74, 29, 57, 43, 61, 58, 66, 46, 1, 39, 40, 61, 76, 77, 40, 21, 100, 58, 65, 20, 96, 42, 42, 95, 40, 72, 68, 49, 27, 14, 53]
OK
----------------------------------------------------------------------------------------------------
95 [32, 21, 83, 50, 79, 36, 8, 57, 84, 80, 37, 54, 7, 25, 51, 25, 76, 68, 40, 20, 43, 20, 13, 72, 98, 61, 36, 71, 34, 1, 92, 27, 76, 19, 45, 21, 80, 77, 98, 38, 30, 30, 50, 45, 35, 94, 19, 82, 44, 26, 28, 3, 53, 30, 42, 48, 99, 17, 95, 67, 44, 48, 78, 99, 97, 76, 61, 26, 1, 78, 30, 53, 58, 88, 65, 23, 73, 38, 29, 1, 43, 23, 70, 41, 29, 39, 63, 56, 46, 85, 33, 81, 95, 36, 11]
OK
----------------------------------------------------------------------------------------------------
59 [72, 10, 81, 90, 43, 44, 7, 79, 17, 47, 79, 9, 13, 87, 8, 71, 28, 56, 32, 49, 61, 20, 53, 15, 75, 50, 55, 16, 55, 54, 82, 58, 18, 35, 82, 55, 47, 35, 52, 47, 96, 60, 49, 16, 25, 57, 79, 16, 65, 52, 37, 68, 68, 100, 59, 88, 51, 95, 72]
OK
----------------------------------------------------------------------------------------------------
43 [65, 76, 27, 31, 24, 42, 81, 100, 32, 46, 43, 66, 20, 34, 80, 10, 26, 6, 87, 88, 86, 8, 98, 62, 26, 45, 85, 74, 19, 61, 1, 72, 19, 87, 20, 64, 66, 57, 55, 20, 20, 92, 62]
OK

パターン３：積の総和（ΣΣAi×Aj）

問題

$A_1, A_2, … , A_n$という数列が与えられた場合に、以下の値を求めなさい

$$
\sum_{i=1}^{N} \sum_{j = i+1}^{N} A_i \times A_j
$$

解法

$A_1$に対する乗算、$A_2$に対する乗算と見ていくと以下のようにまとめることができます。

$$\begin{eqnarray}
A_1\times A_2 + A_1\times A_3 + A_1\times A_4 + … + A_1 \times A_n\\
= A_1(A_2 + A_3 + A_4 + … + A_n)\\
A_2\times A_3 + … + A_2 \times A_n\\
= A_2(A_3 + ….. + A_n)\\
\end{eqnarray}$$

ここから、$A_1$に対しては$\sum_{i = 2}^{n}$までの総和と乗算、$A_2$については、$\sum_{i = 3}^{n}$までの乗算となることがわかります。

プログラミングする場合は、あらかじめ$A_1$ ~ $A_n$までの総和を求めておき、手前の要素から１ずつ引きながら掛け算をしていくだけで求めることができます。

n = 5
a = [5, 2, 4, 6, 1]

tot = sum(a)
ans = 0
for i in range(n) :
    tot -= a[i]
    ans += a[i] * tot

パターン４：区間和の最大値を求める

解法

$A_1, A_2, …, A_n$の区間[l, r]の和の最大値を求める問題です。

この問題は累積和で考えるとわかりやすいです。

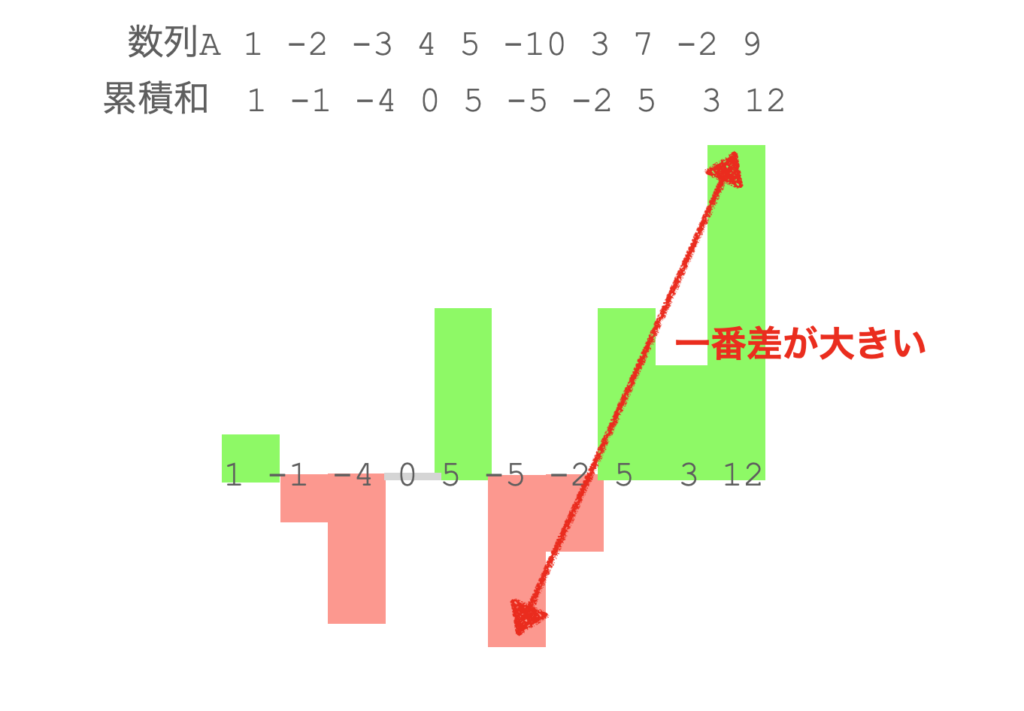
数列A = [1, -2, -3, 4, 5, -10, 3, 7, -2, 9]の場合について考えます。

累積和は下図のようになります。

この図を見ると、区間和の最大は区間差が一番大きい部分であることがわかります。

i番目までみた場合の累積和の最小値から最大値までが最大です

プログラム

下のプログラムは愚直解と、それを高速化したものです。

愚直にやると、開始位置をiにして最後まで加算しながら最大値を求める処理を行うことになるため、２重ループになります。

一方、高速な手法は、O(N)で計算できています。

愚直解のコード

i番目の要素からスタートする区間和を全て計算しています。

a = [1, -2, -3, 4, 5, -10, 3, 7, -2, 9]

# 愚直解
ans = sum(a)
for i in range(len(a)):
    tot = 0
    for j in range(i, len(a)) :
        tot += a[j]
        ans = max(ans, tot)
    
print(ans)

高速な手法のコード

cur_sumは累積和です。min_sumはi番目までの要素の中で最も累積和が小さかった地点の値です。現在地点の区間和はcur_num - min_sumで計算できるので、区間和が最大の場合ansを更新する処理を繰り返しています。


# 高速な解法
a = [1, -2, -3, 4, 5, -10, 3, 7, -2, 9]
cur_sum, min_sum = 0,0
ans = sum(a)
for i in range(len(a)) :
    cur_sum += a[i]
    min_sum = min(min_sum, cur_sum)
    ans = max(ans, cur_sum-min_sum)

print(ans)