MENU
プログラミング
記事内に商品プロモーションを含む場合があります

ヒープと優先キューの作り方をGolangで学ぼう｜ジェネリクス対応版

Aru

ヒープの基本を理解するために、ヒープとヒープを用いた優先キューをGolangで実装してみました。さらに、ジェネリクスを活用して複数の型に対応できるものにしてみました。優先キューがどのように実装されているのか、理解の助けになれば幸いです。

記事の内容を拡張してパッケージ化したコードをGithubに置いています。importして利用できます。

https://github.com/aruaru0/priorityqueue

Contents
  1. ヒープとは
  2. 優先キューとは
  3. まとめ

ヒープとは

ヒープは、完全二分木で表現されるデータ構造の一種であり、各ノードの値がその子ノードの値よりも常に小さい（または大きい）という性質を持っています。この性質により、最小値や最大値を効率的に取り出すことができます。ヒープは主にヒープソートや優先度キューの実装に利用され、データの追加や削除が対数時間で行えるため、効率的な操作が可能です。特に、大量のデータを扱う際やリアルタイムの処理において、その高速性と整列性が大いに役立ちます。

ヒープは配列上に実装することが可能です。この場合、各木のノードと配列のインデックスは以下のように対応します。

配列のインデックス（要素の番号）を１始まりで考えると、ルートノードはインデックス１になります。あるノードのインデックスをiとすると、子は2*i, 2*i+1になります。このように規則的に配置していくことで、配列上にヒープを構成することが可能です。なお、親のインデックスは、このインデックスをiとすると、i/2で調べることができます。

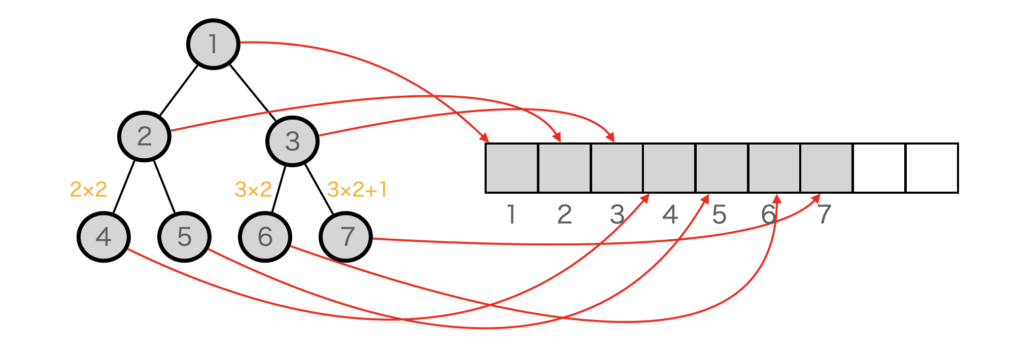
0始まりの配列のインデックスに変換する場合は、ノード番号からインデックスへの変換は-1, インデックスからノード番号への変換は+1すればOKです。

優先キューとは

優先キューは、各要素に優先度が付与されたデータ構造で、高い優先度を持つ要素が優先的に処理されます。これにより、優先度に応じて効率的にデータを管理できます。例えば、最も小さい値から優先して取り出すなどを実現することができます。

優先キューは経路探索（ダイクストラ法）などで利用されます。ヒープは優先キューの実装に適しています。今回は、ヒープをつかって優先キューを実装してみます。

優先キューでは、ヒープへのデータの追加（Push）と、取り出し（Pop）を実装することになります。以下では、この２つの処理の手順を図を使いながら説明したいと思います。

追加の処理（Push）

10→3→16→1と順番に追加していく場合を考えます。

最初は要素がないので先頭に10が入ります。

次に3を追加します。まず3を末尾に追加します。ここで3と親である10を比較すると3の方が小さいので3と10を入れ替えます。入れ替え先には親がないので、これで終了します。

次に16を追加します。まず、16を末尾に追加します。親は3で16よりも小さいので、入れ替えは行わず追加は終了します。

1を追加します。まず、１を末尾に追加します。親は10で1より大きいので入れ替えます。さらに親を見ると3で1より大きいので入れ替えます。入れ替え先には親がないので、これで終了します。

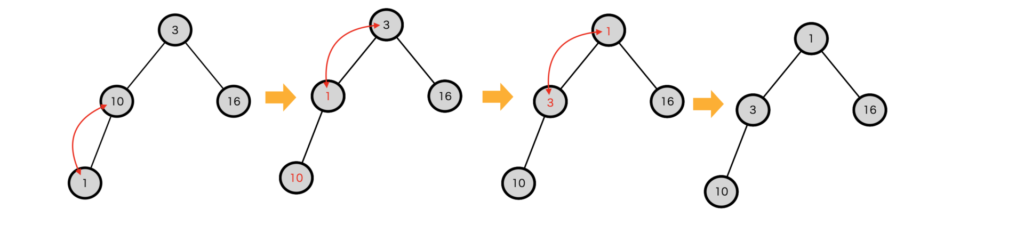
以上の操作を行うことで、各ノードの子を見ると、必ず親の方が小さい値となるデータ構造が保証されます。

取り出しの処理（Pop）

取り出しの手順を説明します。

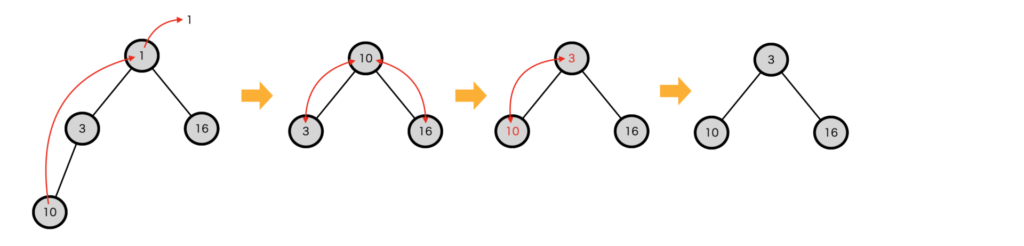
ルートノードが一番小さい値なので、ルートノードの値を取り出します。

新しいルートノードが必要になりますが、暫定的に末尾の値をルートノードに移動させます（末尾のノードは削除します）。

次に子ノードとの大小比較を行い、最も小さい値のノードと親ノードの値を交換します。交換が発生した場合は、交換したノードを親ノードとして同じ操作を端点のノードまで繰り返します。

これで、必ず親の方が小さい値となるデータ構造が保証されます。

プログラムと解説

上記のアルゴリズムを実際にGo言語を使ってプログラミングしてみます。せっかくなので、ジェネリクスを使って、いろいろな型の優先キューが作れるコードにしたいと思います。

Queueの定義

Queue型を定義します。ジェネリクスを使って定義していますが、ここでは、大小比較が可能な型のみを受けいることができるようにしています。これはLess関数で比較ができるものに型を限るためです。

type Queue[T cmp.Ordered] []T

Less, Len, Swap

  • Less：大小比較をした結果を返します。ここでは昇順で並べ替えます。符号を逆にすれば降順になります。
  • Len：キューの長さを返す関数です
  • Swap：２つの要素を入れ替える関数です
func (q Queue[T]) Less(i, j int) bool {
	return q[i] < q[j]
}

func (q Queue[T]) Len() int {
	return len(q)
}

func (q Queue[T]) Swap(i, j int) {
	q[i], q[j] = q[j], q[i]
}

Push

Push関数では、新しい要素を末尾に追加します。その後、親となるデータとの比較を行い、追加した値が小さい場合は、親とスワップします。親が小さい場合はそこで終了です。

func (q *Queue[T]) Push(x T) {
	*q = append(*q, x)
	cur := q.Len()
	parent := cur / 2
	for cur != 1 {
		if q.Less(cur-1, parent-1) {
			q.Swap(cur-1, parent-1)
		} else {
			break
		}
		cur = parent
		parent = cur / 2
	}
}

Pop

Pop関数では、まず先頭の要素を保存します。次に、末尾のデータを先頭に代入し、末尾の要素を削除します。あとは、先頭から子のノードとの大小比較を行い、子の方が小さい場合はいれかをを行います。Pop関数の場合は、子ノードが２つある場合はより小さい方とスワップします。なお、子ノードが１つしかない場合のケアも必要です。

func (q *Queue[T]) Pop() T {
	old := *q
	n := len(old)
	item := old[0]

	old[0] = old[n-1]
	old = old[:n-1]
	cur := 1
	for {
		nxt0 := cur * 2
		nxt1 := cur*2 + 1
		if nxt0 > len(old) {
			break
		}
		nxt := nxt0
		if nxt1 <= len(old) && old.Less(nxt1-1, nxt0-1) {
			nxt = nxt1
		}
		if old.Less(nxt-1, cur-1) {
			old.Swap(nxt-1, cur-1)
		} else {
			break
		}

		cur = nxt
	}

	*q = old
	return item
}

利用例

以下、利用例です。int型とstring型でテストしてます。

func main() {

	var q = make(Queue[int], 0)

	q.Push(10)
	fmt.Println(q)
	q.Push(3)
	fmt.Println(q)
	q.Push(16)
	fmt.Println(q)
	q.Push(5)
	fmt.Println(q)
	q.Push(2)
	fmt.Println(q)
	q.Push(20)
	fmt.Println(q)
	q.Push(4)
	fmt.Println(q)
	q.Push(8)
	fmt.Println(q)
	q.Push(1)
	fmt.Println(q)

	for len(q) != 0 {
		fmt.Println(q.Pop(), q)
	}

	sq := Queue[string]{}
	sq.Push("zzz")
	sq.Push("ttt")
	sq.Push("bbb")
	sq.Push("xxx")
	sq.Push("aaa")
	for len(sq) != 0 {
		fmt.Println(sq.Pop(), sq)
	}
}

実行結果のように、小さい順に出力されていることがわかります（文字列の場合は、辞書順で出力されています）。

実行結果
[10]
[3 10]
[3 10 16]
[3 5 16 10]
[2 3 16 10 5]
[2 3 16 10 5 20]
[2 3 4 10 5 20 16]
[2 3 4 8 5 20 16 10]
[1 2 4 3 5 20 16 10 8]
1 [2 3 4 8 5 20 16 10]
2 [3 5 4 8 10 20 16]
3 [4 5 16 8 10 20]
4 [5 8 16 20 10]
5 [8 10 16 20]
8 [10 20 16]
10 [16 20]
16 [20]
20 []
aaa [bbb xxx ttt zzz]
bbb [ttt xxx zzz]
ttt [xxx zzz]
xxx [zzz]
zzz []

プログラム全体

以下は、今回の実験のプログラム全体です。

package main

import (
	"cmp"
	"fmt"
)

// Queue ... 実装例
type Queue[T cmp.Ordered] []T

func (q Queue[T]) Less(i, j int) bool {
	return q[i] < q[j]
}

func (q Queue[T]) Len() int {
	return len(q)
}

func (q Queue[T]) Swap(i, j int) {
	q[i], q[j] = q[j], q[i]
}

func (q *Queue[T]) Push(x T) {
	*q = append(*q, x)
	cur := q.Len()
	parent := cur / 2
	for cur != 1 {
		if q.Less(cur-1, parent-1) {
			q.Swap(cur-1, parent-1)
		} else {
			break
		}
		cur = parent
		parent = cur / 2
	}
}

func (q *Queue[T]) Pop() T {
	old := *q
	n := len(old)
	item := old[0]

	old[0] = old[n-1]
	old = old[:n-1]
	cur := 1
	for {
		nxt0 := cur * 2
		nxt1 := cur*2 + 1
		if nxt0 > len(old) {
			break
		}
		nxt := nxt0
		if nxt1 <= len(old) && old.Less(nxt1-1, nxt0-1) {
			nxt = nxt1
		}
		if old.Less(nxt-1, cur-1) {
			old.Swap(nxt-1, cur-1)
		} else {
			break
		}

		cur = nxt
	}

	*q = old
	return item
}

func main() {

	var q = make(Queue[int], 0)

	q.Push(10)
	fmt.Println(q)
	q.Push(3)
	fmt.Println(q)
	q.Push(16)
	fmt.Println(q)
	q.Push(5)
	fmt.Println(q)
	q.Push(2)
	fmt.Println(q)
	q.Push(20)
	fmt.Println(q)
	q.Push(4)
	fmt.Println(q)
	q.Push(8)
	fmt.Println(q)
	q.Push(1)
	fmt.Println(q)

	for len(q) != 0 {
		fmt.Println(q.Pop(), q)
	}

	sq := Queue[string]{}
	sq.Push("zzz")
	sq.Push("ttt")
	sq.Push("bbb")
	sq.Push("xxx")
	sq.Push("aaa")
	for len(sq) != 0 {
		fmt.Println(sq.Pop(), sq)
	}
}

まとめ

以上、自作の優先キューを作成する方法について解説しました。Go言語にはheapのライブラリがあるので、普段はそちらを使いますが、自作することで理解が深まるかと思います。個人的にはジェネリクスの練習になりました。

Go言語の標準パッケージを使って、PriorityQueueを作る方法については、以下を参照してください。

あわせて読みたい
Go言語でAtCoder｜スタック、キュー、 優先キューの実装方法
Go言語でAtCoder｜スタック、キュー、 優先キューの実装方法

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

ABOUT ME
ある/Aru
ある/Aru
IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)
Contact
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
Recommend
こちらの記事もどうぞ
記事URLをコピーしました