2023.12.09 2024.09.13

記事内に商品プロモーションを含む場合があります

【Python】ローリングハッシュをセグメント木に載せる｜部分文字列の一致を高速にチェック

Aru

部分文字列の一致を調べる方法として、ローリングハッシュがあります。更新文字が更新される場合に部分文字列の一致を高速に調べるにはどうすれば良いでしょうか。実は、ローリングハッシュはセグメント木に載せることができます。この記事では、ローリングハッシュをセグメント木上に実装する方法について紹介します。

Contents

ローリングハッシュとは
セグメント木
- セグメント木の使い方
ローリングハッシュをセグメント木にのせる
まとめ

ローリングハッシュとは

ローリングハッシュは、要素iを$S_i$、xを任意の整数、pを素数した場合に以下の式で計算されるハッシュになります。

$$
hash(S) = \sum_{i=0}^N{S_i \times x^i} (mod \ p)
$$

$S = {S_0, S_1, S_2, S_3}$のとき、$hash(S)$は以下になります。

$$
hash(S) = S_0 + S_1 x + S_2 x^2 + S_3 x^3 (mod \ p)
$$

ここで、$S’ = {S_2, S_3}$のハッシュ値を求めたい場合は、以下のように計算できます。

$$
\begin{eqnarray}
hash({S2,S3})&=&\frac{hash(S_0, S_1, S_2, S_3) – hash({S_0, S_1})}{x^2} \\
&=& \frac{S_0 + S_1 x + S_2 x^2 + S_3 x^3 – S_0 + S_1 x}{x^2} \\
&=& S_2 + S_2 x
\end{eqnarray}
$$

$hash(S_0), hash(S_0, S_1), …, hash(S_0,…,S_N)$の値を持っていれば、区間のハッシュ値が簡単に計算できるというのがローリングハッシュの強みです。

セグメント木

ここでは、セグメント木の説明は省略します。

Pythonのセグメント木の実装としては、「ACL-for-python」のセグメント木がありますのでこれを利用します。

コードは以下になります。

class segtree():
    n=1
    size=1
    log=2
    d=[0]
    op=None
    e=10**15
    def __init__(self,V,OP,E):
        self.n=len(V)
        self.op=OP
        self.e=E
        self.log=(self.n-1).bit_length()
        self.size=1<<self.log
        self.d=[E for i in range(2*self.size)]
        for i in range(self.n):
            self.d[self.size+i]=V[i]
        for i in range(self.size-1,0,-1):
            self.update(i)
    def set(self,p,x):
        assert 0<=p and p<self.n
        p+=self.size
        self.d[p]=x
        for i in range(1,self.log+1):
            self.update(p>>i)
    def get(self,p):
        assert 0<=p and p<self.n
        return self.d[p+self.size]
    def prod(self,l,r):
        assert 0<=l and l<=r and r<=self.n
        sml=self.e
        smr=self.e
        l+=self.size
        r+=self.size
        while(l<r):
            if (l&1):
                sml=self.op(sml,self.d[l])
                l+=1
            if (r&1):
                smr=self.op(self.d[r-1],smr)
                r-=1
            l>>=1
            r>>=1
        return self.op(sml,smr)
    def all_prod(self):
        return self.d[1]
    def max_right(self,l,f):
        assert 0<=l and l<=self.n
        assert f(self.e)
        if l==self.n:
            return self.n
        l+=self.size
        sm=self.e
        while(1):
            while(l%2==0):
                l>>=1
            if not(f(self.op(sm,self.d[l]))):
                while(l<self.size):
                    l=2*l
                    if f(self.op(sm,self.d[l])):
                        sm=self.op(sm,self.d[l])
                        l+=1
                return l-self.size
            sm=self.op(sm,self.d[l])
            l+=1
            if (l&-l)==l:
                break
        return self.n
    def min_left(self,r,f):
        assert 0<=r and r<=self.n
        assert f(self.e)
        if r==0:
            return 0
        r+=self.size
        sm=self.e
        while(1):
            r-=1
            while(r>1 and (r%2)):
                r>>=1
            if not(f(self.op(self.d[r],sm))):
                while(r<self.size):
                    r=(2*r+1)
                    if f(self.op(self.d[r],sm)):
                        sm=self.op(self.d[r],sm)
                        r-=1
                return r+1-self.size
            sm=self.op(self.d[r],sm)
            if (r& -r)==r:
                break
        return 0
    def update(self,k):
        self.d[k]=self.op(self.d[2*k],self.d[2*k+1])
    def __str__(self):
        return str([self.get(i) for i in range(self.n)])

セグメント木の使い方

使い方は、詳しくは、こちらのドキュメントを参照してください。ここでは、今回使う関数だけ説明します。

初期化

セグメントツリーを初期化します

G=segtree(list,func,ide_ele)

listは初期値のリストです。

funcはセグメント木で行う演算です。演算は例えば以下のような計算になります。

演算は、モノイドである必要があります。モノイドとは、結合法則が成り立ち、単位元が存在する演算です

とりあえず、加算、乗算、min, maxなどの演算はセグメント木にのせることができます。

def add(x,y):
    return x+y

ide_eleは単位元です。加算の場合は、0になります。

以下、セグメント木の初期化の例です（ドキュメントから抜粋）

#加算
def add(x,y):
    return x+y
G=segtree(LIST,add,0)


#乗算
G=segtree(LIST,(lambda x,y:x*y),1)

#最大
G=segtree(LIST,min,INF)

#最小
G=segtree(LIST,max,-INF)

set

p番目に値を設定します

G.set(p,x)

get

p番目の値を返します

G.get(p)

prod

[l,r)の範囲内での演算した結果を返します。

G.prod(l,r)

ローリングハッシュをセグメント木にのせる

基本的な考え方

数列Sのi番目の値をS(i)として考えます。

i番目の要素とi+1番目の要素２つのローリングハッシュを計算する場合は、S(i) + S(i+1) * xを計算することになります。さらに、i+2番目の要素を加える場合は、S(i) + S(i+1) * x + S(i+2)*x^2となります。

結論から言いますが、ローリングハッシュの値と、x^{ローリングハッシュに使った要素数}の値を保持していれば、２つのローリングハッシュの値を結合することができます。

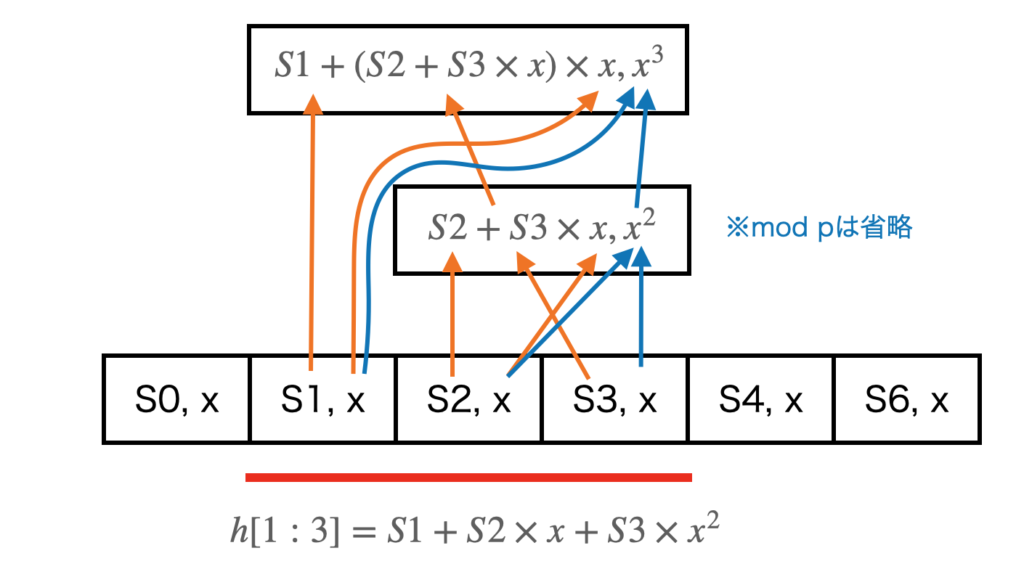
下図は、S[1:3]とS[2:4]を計算する場合の例です。

各要素を（Si, x）の組みで初期化しておきます。するとS2とS3のローリングハッシュは下図のように計算できます。これにS1を加えればS1~S3の区間のローリングハッシュが計算できます。

オレンジの矢印がハッシュ値の計算、青い矢印がx^{ローリングハッシュに使った要素数}の計算です

また、S2~S4の区間の計算を行う場合は、上と同様に計算したS2, S3のローリングハッシュにS4を加えることで計算することができます。

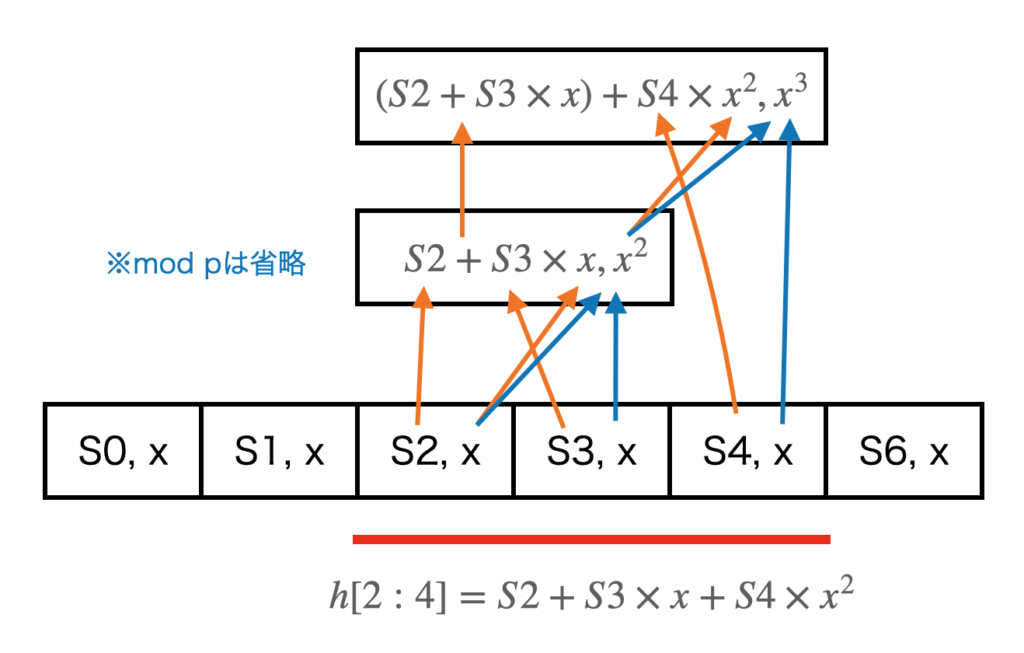
この操作は、セグメント木に実装することができます。以下、セグメント木にハッシュ計算を実装してみます。

実装方法

格納するデータ

まず、セグメント木にのせる値を考えます。上の例のように、ハッシュ計算した結果と、x^{計算に使った要素数}を記録しておけばよさそうです。今回は、これに加えてmod pする素数も記録してきます。したがって、記録するデータは以下になります。

（ハッシュ計算値、x^{計算に使った要素数}, 素数p）

素数pも入れている理由は後で書きます

演算`func`

演算は、上に書いた図の通りのものになります

def op(x, y) :
    h0, x0, p = x
    h1, x1, p = y
    return [(h0 + h1 * x0)%p, (x0*x1)%p, p]

単位元

単位元は（0,1,p）になります

セグメント木の生成

格納するデータ、演算、単位元が決まったので、セグメント木を生成するだけです。

sを記録データのリストとした場合、セグメント木のオブジェクトの生成コードは以下になります。

segS = segtree(s, op, [0,1,p])

AtCoder ABC331-F問題を解く

ローリングハッシュをセグメント木に実装する方法を説明しました。ここでは、これを使ってAtCoderのABC331のF問題を解いてみます。

この問題は、区間が回文になっているかどうかをYes, Noで答える問題です。

区間[l, r)が回文になっているかどうかは、文字列Sの[l, r)と、文字列Sを逆から並べた文字列Tの[N-r, N-l)が一致しているかどうかを調べることで分かります。

ハッシュ関数を使う場合、文字列Sの[l, r)のハッシュ値と、文字列Sを逆から並べた文字列Tの[N-r, N-l)のハッシュ値が一致していることを調べれば良いことになります。

この問題では、文字列の書き換えがありますので、文字列を書き換えた結果のハッシュ値も高速に計算する必要があります。

この問題は、文字列Sと、文字列Sを逆から並べた文字列Tの、2つのセグメント木を使うことで解くことができます。

以下、コードです（pypyでACすることを確認済みです）

# --- セグメント木 -----
class segtree():
    n=1
    size=1
    log=2
    d=[0]
    op=None
    e=10**15
    def __init__(self,V,OP,E):
        self.n=len(V)
        self.op=OP
        self.e=E
        self.log=(self.n-1).bit_length()
        self.size=1<<self.log
        self.d=[E for i in range(2*self.size)]
        for i in range(self.n):
            self.d[self.size+i]=V[i]
        for i in range(self.size-1,0,-1):
            self.update(i)
    def set(self,p,x):
        assert 0<=p and p<self.n
        p+=self.size
        self.d[p]=x
        for i in range(1,self.log+1):
            self.update(p>>i)
    def get(self,p):
        assert 0<=p and p<self.n
        return self.d[p+self.size]
    def prod(self,l,r):
        assert 0<=l and l<=r and r<=self.n
        sml=self.e
        smr=self.e
        l+=self.size
        r+=self.size
        while(l<r):
            if (l&1):
                sml=self.op(sml,self.d[l])
                l+=1
            if (r&1):
                smr=self.op(self.d[r-1],smr)
                r-=1
            l>>=1
            r>>=1
        return self.op(sml,smr)
    def all_prod(self):
        return self.d[1]
    def max_right(self,l,f):
        assert 0<=l and l<=self.n
        assert f(self.e)
        if l==self.n:
            return self.n
        l+=self.size
        sm=self.e
        while(1):
            while(l%2==0):
                l>>=1
            if not(f(self.op(sm,self.d[l]))):
                while(l<self.size):
                    l=2*l
                    if f(self.op(sm,self.d[l])):
                        sm=self.op(sm,self.d[l])
                        l+=1
                return l-self.size
            sm=self.op(sm,self.d[l])
            l+=1
            if (l&-l)==l:
                break
        return self.n
    def min_left(self,r,f):
        assert 0<=r and r<=self.n
        assert f(self.e)
        if r==0:
            return 0
        r+=self.size
        sm=self.e
        while(1):
            r-=1
            while(r>1 and (r%2)):
                r>>=1
            if not(f(self.op(self.d[r],sm))):
                while(r<self.size):
                    r=(2*r+1)
                    if f(self.op(self.d[r],sm)):
                        sm=self.op(self.d[r],sm)
                        r-=1
                return r+1-self.size
            sm=self.op(self.d[r],sm)
            if (r& -r)==r:
                break
        return 0
    def update(self,k):
        self.d[k]=self.op(self.d[2*k],self.d[2*k+1])
    def __str__(self):
        return str([self.get(i) for i in range(self.n)])
    

# ----- ここからメインプログラム　--------
N, Q = map(int, input().split())

# 文字列Sと逆順のTを作成。同時に整数値に変換
s = [ord(c) for c in list(input())]
t = s[::-1]

# 素数
p = 998244353

# xをランダムに生成
import random
x = random.randint(10000, p) % p

# セグメント木にのせるデータに変換
s = [[e, x, p] for e in s]
t = [[e, x, p] for e in t]

# funcの定義
def op(x, y) :
    h0, x0, p = x
    h1, x1, p = y
    return [(h0 + h1 * x0)%p, (x0*x1)%p, p]

# セグメント木の生成
segS = segtree(s, op, [0,1,p])
segT = segtree(t, op, [0,1,p])

# ループ
for _ in range(Q) :
    v = input().split()
    if v[0] == '1' :
        pos, c = int(v[1])-1, ord(v[2])
        segS.set(pos, [c, x, p])
        segT.set(N-1-pos, [c, x, p])
    else :
        l, r = int(v[1])-1, int(v[2])
        h0 = segS.prod(l, r)[0]
        h1 = segT.prod(N-r, N-l)[0]
        if h0 == h1 :
            print("Yes")
        else:
            print("No")

データにmod pの値を入れた理由

ハッシュ関数を用いた比較の場合、違う文字列が同じ値になる衝突が発生する可能性があります。

これを回避する方法として、異なる素数で計算したハッシュ値を用意し、どの素数でも２つの部分文字列のハッシュ値のペアのハッシュ値一致している場合に、一致しているとすることで衝突確率を減らすことができます。

要は、複数組みのペアを用意しておいて、全部一致している時に一致と判断する方法です

それぞれのペアの素数は、変えておきます。

F問題も衝突を気にしていて、もしWAが出たらセグメント木を複数組用意する予定でした。

衝突確率はそれなりにありそうだったので、衝突するかと思いましたがACしたので１組だけの判定で済みました。

まとめ

セグメント木に、ローリングハッシュをのせる方法について解説しました。

ABC331-F問題を解くときに、自分自身のローリングハッシュの理解が足りずん苦戦したので、整理がてら記事にしました。

参考になれば幸いです。

#AtCoder #python #rolling hash #segtree #セグツリー #セグメント木 #ローリングハッシュ

【Python】ローリングハッシュをセグメント木に載せる｜部分文字列の一致を高速にチェック

ローリングハッシュとは

セグメント木

セグメント木の使い方

初期化

set

get

prod

ローリングハッシュをセグメント木にのせる

基本的な考え方

実装方法

格納するデータ

演算`func`

単位元

セグメント木の生成

AtCoder ABC331-F問題を解く

データにmod pの値を入れた理由

まとめ

コメントをキャンセル

A*アルゴリズムで効率良く最短経路を探索｜Pythonによる実装

Google Colabの生成AI機能によるコード作成支援の使い方

Pandasで大規模データを扱う時にメモリ消費を抑える手法を紹介

【Python】CSVファイルの中身を簡単に翻訳する方法（deep-translator）

ローリングハッシュとは

セグメント木

セグメント木の使い方

初期化

set

get

prod

ローリングハッシュをセグメント木にのせる

基本的な考え方

実装方法

格納するデータ

演算func

単位元

セグメント木の生成

AtCoder ABC331-F問題を解く

データにmod pの値を入れた理由

まとめ

コメントをキャンセル

A*アルゴリズムで効率良く最短経路を探索｜Pythonによる実装

Google Colabの生成AI機能によるコード作成支援の使い方

Pandasで大規模データを扱う時にメモリ消費を抑える手法を紹介

【Python】CSVファイルの中身を簡単に翻訳する方法（deep-translator）

演算`func`