数列の区間最大値を高速に列挙する方法（Python）

Aru

この記事では、競技プログラミングやアルゴリズム問題で頻出の「区間最大値」を高速に列挙する方法をPythonで解説します。ここでは、優先キューを活用する方法と、さらに高速な方法の２つを紹介します。

Contents

数列の区間最大値の問題とは
- 優先キュー（Priority Queue）を使った解法
- O(N)の解法
まとめ

数列の区間最大値の問題とは

区間最大値の問題とは、「N個の要素を持つ数列の連続するK個の要素の最大値を全て求める」問題です。例えば、[1, 3, -1, -3, 5, 3, 6, 7]という数列でK=3の場合は、最初は[1,3,-1]で3、次は1つずらして[3,-1, -3]の最大値で3と１つずつスライドしながら区間最大値を計算していく問題です。上記の例では、結果は[3, 3, 5, 5, 6, 7]となります。

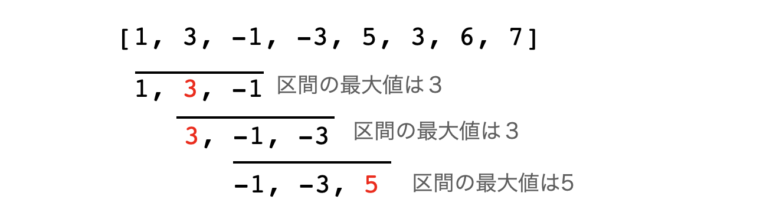
この問題を愚直に実装すると、スタートする場所はN-K箇所で、そこからK個の最大値を調べるのでK(N-K)回の演算が必要になります（計算量はO(NK)）。Nが$10^5$、Kが$10^3$の場合、おおよその計算量は$10^8$となるので処理に時間がかかってしまいます。

これを高速に解くのが「区間最大値の列挙」問題です。

ここでは、２つの解法を紹介します。

どちらも、尺取り法と言われる方法になります。

優先キュー（Priority Queue）を使った解法

最初に紹介するのは優先キュー（Priority Queue）を利用する方法です。

優先キューの使い方

要素の値とインデックスを優先キューに入れます
Python標準ライブラリのheapqは、要素を最小値順にソートします。区間最大値問題を解くためには、最大値順で管理する必要がありますので、値とインデックスをペア（優先度, インデックス）として格納し、以下のように正負反転した値(-val)を入力します

ウィンドウの移動

現在の要素を優先キュー（max_heap）に追加します
ウィンドウが左にずれたとき、ヒープの先頭にある要素のインデックスが範囲外（i - k）になっていれば、その要素をヒープから削除します。これにより、ヒープの先頭は範囲内の最大値となります

結果の追加:

ヒープのトップ（max_heap[0]）を結果リストに追加します

このプログラムの演算量はO(NlogN)となります。

import heapq

def max_k(nums, k):
    if not nums or k == 0:
        return []

    result = []
    max_heap = []
    for i in range(len(nums)):
        heapq.heappush(max_heap, (-nums[i], i))

        if i >= k - 1:
            while max_heap[0][1] <= i - k:
                heapq.heappop(max_heap)
            result.append(-max_heap[0][0])

    return result

print(max_k([1, 3, -1, -3, 5, 3, 6, 7], 3))
# [3, 3, 5, 5, 6, 7]

上記のプログラムでは、最大値は以下のようになりますが、結果は一致します。

[1, 3, -1] → 最大値は 3
[3, -1, -3] → 最大値は 3
[ -1, -3, 5] → 最大値は 5
[ -3, 5, 3] → 最大値は 5
[5, 3, 6] → 最大値は 6
[3, 6, 7] → 最大値は 7

O(N)の解法

次に紹介するのは計算量O(N)となる解法です。

from collections import deque

def max_k(nums, k):
    if not nums:
        return []
    
    result = []
    deq = deque()
    
    for i in range(len(nums)):
        if deq and deq[0] < i - k + 1:
            deq.popleft()
        
        while deq and nums[deq[-1]] < nums[i]:
            deq.pop()
        deq.append(i)

        if i >= k - 1:
            result.append(nums[deq[0]])
    
    return result

print(max_k([1, 3, -1, -3, 5, 3, 6, 7], 3))
# [3, 3, 5, 5, 6, 7]

このプログラムは、N回の繰り返しで終了するのでO(N)です。

動作を確認していきます。ここで、deqには、要素のインデックスが格納されていきます。

範囲外の要素を`deq`から削除する

現在の場所iからk個以上前のインデックスを削除します。これによりdeqの範囲はk個内の値となります。

        if deq and deq[0] < i - k + 1:
            deq.popleft()

新たに追加する要素より小さな値は削除する

ここがポイントになります。deqの末尾の要素の値（nums[def[-1]]）と現在の値（nums[i]）の値を比較して、現在の値が大きければ末尾の値を削除しています。新たに入力される値の方がdeqに格納されているインデックスが示す値より大きいのであれば、その値は範囲の最大値となることはないので削除してOKだからです。削除後、自身のインデックス追加しています。

        while deq and nums[deq[-1]] < nums[i]:
            deq.pop()
        deq.append(i)

幅がK個になったら最大値を結果に追加

上記の２つの操作により、「deqは、k個の範囲の値」かつ「先頭は区間で最大となる値のインデックス」であることが保証されていますので、先頭の値を結果に追加するだけで区間最大値を追加することが可能です。

        if i >= k - 1:
            result.append(nums[deq[0]])

理解できない場合は、途中にprint(deq)などを入れて確認してみると良いかと思います。

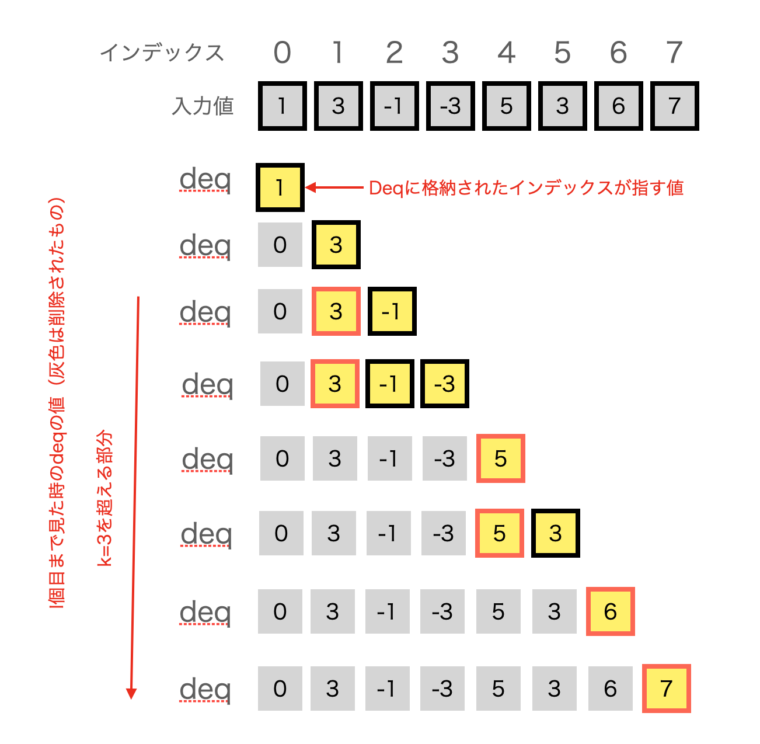
一応、挙動を示す図を入れておきます。わかりにくいかもしれませんがdeqの内部の状態です。
deqは要素のインデックスが格納されていますが、わかりやすいようにインデックスが指す要素の値を書いています。また、黄色いものがi番目まで見た時に格納されている値、灰色のものが格納されたが削除されたものです。deqの状態は上から1番目の要素の入力後、２番目の要素の入力後・・・となります。出力は、赤枠の数値です。