2023.12.17

記事内に商品プロモーションを含む場合があります

巡回セールスマン問題のソルバー「LKH-3」の使い方を解説

tadanori

LKH-3は巡回セールスマン問題の近似解を求めるプログラムです。ドキュメントはあるのですが、説明が少なく、どこから触って良いかわからない感じなので、基本的な使い方を記事にしてみました。

Contents

LKH-3とは
LKHの特徴
インストール
簡単な使い方
２次元マップの座標で入力
マトリクスで入力
その他TIPS
- 初期ツアーファイルが設定できる
まとめ

LKH-3とは

K. HelsgaunによるLin-Kernighan-Helsgaun法(LKH法)の実装です。LKH法は、有名な巡回セールスマン問題（TSP）を解くアルゴリズムで、これをソフトウェアとして実装したものになります。

ホームページを見ると、Version 3.0.9（June 2023）となっており、現在も更新されていることがわかります。

LKH-3のホームページ
http://webhotel4.ruc.dk/~keld/research/LKH-3/

ライセンスについて

ホームページの最後の方に、以下のように書かれています。

“The code is distributed for academic and non-commercial use. The author reserves all rights to the code.”

学術と商用利用以外は利用可能ということです。

LKHの特徴

公式に書かれているわけではありませんが、実際に使った感想を含め特徴を書きます

高速

巡回セールスマンのソルバーとして高速です。Googleが開発しているOR-Toolsなどと比較しても高速に近次解を求めることができます。高速だからといって、解の精度が低いわけでもありません。

慣れるまで、若干使いにくいですが、高速性はかなり魅力です

巨大な問題に対応できる

訪問先が数千を超える規模の問題に使うことができます（実際に使った実績あり）。実は、思いの外巨大な問題に使うことができたので、びっくしています。

kaggleで使うこともあります。

色々な問題を解ける

TSPだけでなく、色々な問題を解くことができます。公式ページに書かれているものですが、並べるとすごい数です。

知らないものも多いです

今回は、基本的なTSPについて使い方を解説します。

TSP	Symmetric traveling salesman problem（巡回セールスマン問題）
ASTP	Asymmetric traveling salesman problem（非対称循環セールスマン問題）
HCP	Hamiltonian cycle problem（ハミルトンサイクル問題）
HPP	Hamiltonian path problem（ハミルトンパス問題）
ACVRP	Asymmetric capacitated vehicle routing problem（非対称容量制約付き配送計画問題）
ADCVRP	Asymmetric distance constrained vehicle routing problem（非対称距離制約付き配送計画問題）
BWTSP	Black and white traveling salesman problem （白黒巡回セールスマン問題；点に白と黒の属性を付加して，連続する黒の点の長さや位数に対する制約が付加された問題）
CCVRP	Cumulative capacitated vehicle routing problem（累積容量制約付き配送計画問題；各顧客への到着時刻の和を最小化する問題）
CTSP	Colored traveling salesman problem（色付き巡回セールスマン問題；複数のセールスマンは色をもち，訪問する点は色の部分集合をもつ．点は指定したいずれかの色をもつセールスマンによって処理されるという条件が付加された問題）
CVRP	Capacitated vehicle routing problem（容量制約付き配送計画問題）
CVRPTW	Capacitated vehicle routing problem with time windows（時間枠付き容量制約付き配送計画問題）
DCVRP	Distance constrained capacitated vehicle routing problem（距離・容量制約付き配送計画問題）
1-PDTSP	One-commodity pickup-and-delivery traveling salesman problem（1品種・積み込み・積み降ろし巡回セールスマン問題）
m-PDTSP	Multi-commodity pickup-and-delivery traveling salesman problem（複数品種・積み込み・積み降ろし巡回セールスマン問題）
m1-PDTSP	Multi-commodity one-to-one pickup-and-delivery traveling salesman problem （複数品種・1対1・積み込み・積み降ろし巡回セールスマン問題）
MLP	Minimum latency problem（最小待ち時間問題；顧客の待ち時間の和を最小化する巡回セールスマン問題）
MTRP	Multiple traveling repairman problem（複数巡回修理人問題；複数の修理人が顧客を訪問する際の，顧客の待ち時間の和を最小化する問題）
MTRPD	Multiple traveling repairman problem with distance constraints（距離制約付き複数巡回セールスマン問題）
mTSP	Multiple traveling salesmen problem（複数巡回セールスマン問題）
OCMTSP	Open close multiple traveling salesman problem（パス型閉路型混在巡回セールスマン問題；あるセールスマンはデポに戻り，他のセーするマンはデポに戻る必要がないパスで良いと仮定した問題）
OVRP	Open close multiple traveling salesman problem（パス型閉路型混在巡回セールスマン問題；あるセールスマンはデポに戻り，他のセーするマンはデポに戻る必要がないパスで良いと仮定した問題）
OVRP	Open vehicle routing problem（パス型配送計画問題；デポに戻る必要がないと仮定した配送計画問題）
PDPTW	Pickup-and-delivery problem with time windows（時間枠付き積み込み・積み降ろし型配送計画問題）
PDTSP	Pickup-and-delivery traveling salesman problem（積み込み・積み降ろし巡回セールスマン問題）
PDTSPF	Pickup-and-delivery traveling salesman problem with FIFO loading（先入れ先出し型積み込み・積み降ろし巡回セールスマン問題）
PDTSPL	Pickup-and-delivery traveling salesman problem with LIFO loading（後入れ先出し型積み込み・積み降ろし巡回セールスマン問題）
RCTVRP	Risk-constrained cash-in-transit vehicle routing problem（リスク制約付き現金輸送配送計画問題）
RCTVRPTW	Risk-constrained cash-in-transit vehicle routing with time windows（時間枠付きリスク制約付き現金輸送配送計画問題）
SOP	Sequential ordering problem（先行制約付き巡回セールスマン問題）
STTSP	Steiner traveling salesman problem（Steinr巡回セールスマン問題）
TRP	Traveling repairman problem（巡回修理人問題；顧客の待ち時間の和を最小化する問題）
TSPDL	Traveling salesman problem with draft limits（喫水制限付き巡回セールスマン問題）
TSPPD	Traveling salesman problem with pickups and deliveries（喫水制限付き積み込み・積み降ろし巡回セールスマン問題）
TSPTW	Traveling salesman problem with time windows（時間枠付き巡回セールスマン問題）
VRPB	Vehicle routing problem with backhauls（帰り荷を考慮した配送計画問題）
VRPBTW	Vehicle routing problem with backhauls and time windows（帰り荷を考慮した時間枠付き配送計画問題）
VRPMPD	Vehicle routing problem with mixed pickup and delivery（配送と集荷を考慮した配送計画問題）
VRPMPDTW	Vehicle routing problem with mixed pickup and delivery and time windows（配送と集荷を考慮した時間枠付き配送計画問題）
VRPSPD	Vehicle routing problem with simultaneous pickup and delivery（同時配送集荷を考慮した配送計画問題）
VRPSPDTW	Vehicle routing problem with simultaneous pickup-delivery and time windows（同時配送集荷を考慮した時間枠付き配送計画問題）

インストール

ダウンロード

LKH-3は、ダウンロード後にコンパイルしなければなりません。Linux/MacOSなどではまずばC/C++の開発環境をインストールしてください。

その後、LKH-3.0.9.tgzをダウンロードします。Windowsの場合は、実行ファイルがこちらからダウンロード可能です。

ダウンロードしたら、以下のコマンドを使って.tgzファイルを展開します。

% tar xxvf LKH-3.0.9.tgz

make

展開されたディレクトリに移動して、makeコマンドを実行します。

% cd LKH-3.0.9
% make

エラーが出なければLKHというファイルが生成されているはずです。

% ls
DOC              LKH              Makefile         README.txt       SRC              pr2392.par       pr2392.tsp       whizzkids96.atsp whizzkids96.par

動作確認

正常に動作するか確認します。以下のコマンドを実行してください。

% ./LKH whizzkids96.par

正常にインストールされていれば以下のような実行結果が出力されます。

　：
（略）
　：
* 40: Cost = 1244_4933, Gap = 5.1564%, Time = 0.37 sec.
* 57: Cost = 1244_4899, Gap = 5.1564%, Time = 0.54 sec.
* 84: Cost = 1244_4823, Gap = 5.1564%, Time = 0.75 sec.
* 92: Cost = 1244_4797, Gap = 5.1564%, Time = 0.77 sec.
* 96: Cost = 1238_4882, Gap = 4.6492%, Time = 0.80 sec.
* 109: Cost = 1238_4872, Gap = 4.6492%, Time = 0.87 sec.
* 134: Cost = 1198_4748, Gap = 1.2680%, Time = 0.99 sec.
* 139: Cost = 1198_4738, Gap = 1.2680%, Time = 1.01 sec.
* 154: Cost = 1198_4724, Gap = 1.2680%, Time = 1.12 sec.
* 331: Cost = 1198_4708, Gap = 1.2680%, Time = 2.08 sec.
* 2272: Cost = 1197_4750, Gap = 1.1834%, Time = 12.81 sec.
* 2275: Cost = 1193_4746, Gap = 0.8453%, Time = 12.83 sec.
* 2340: Cost = 1191_4744, Gap = 0.6762%, Time = 13.21 sec.
* 2411: Cost = 1183_4715, Gap = 0.0000%, Time = 13.73 sec.
Population:
  1: 1183_4715, Gap = 0.0000%
Run 1: Cost = 1183_4715, Gap = 0.0000%, Time = 13.73 sec.

Successes/Runs = 1/1
Penalty.min = 1183, Penalty.avg = 1183.00, Penalty.max = 1183
Gap.min = 0.0000%, Gap.avg = 0.0000%, Gap.max = 0.0000%
Trials.min = 2411, Trials.avg = 2411.0, Trials.max = 2411
Time.min = 13.73 sec., Time.avg = 13.73 sec., Time.max = 13.73 sec.
Time.total = 13.79 sec.
  Size.min = 28, Size.max = 33, Penalty = 1183
  Cost.min = 1173, Cost.max = 1183, Cost.sum = 4715
Best ATSP solution:
  Cost = 1183_4715

簡単な使い方

パラメータファイルとプロブレムファイル

LKHで巡回セールスマン問題を解く場合、パラメータファイルをプロブレムファイルを作成する必要があります。

パラメータファイル
各種パラメータを設定するファイルです
プロブレムファイル
解きたい問題の内容を記述するファイルです

パラメータファイルの詳しい説明は、LKHのdocフォルダにあります。

doc/LKH-2_USER_GUIDE.pdf
doc/LKH-3_PARAMETERS.pdf

また、プロブレムファイルはTSPLIBと共通みたいです。

LKHのドキュメントにリンク先が書かれていますが、そのリンク先には現在プロブレムファイルのフォーマットのドキュメントがないみたいです。調べたところ、以下にありましたので、そちらを参照してください。

プロブレムファイルのフォーマットのドキュメント
http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp95.pdf

パラメータファイルの書き方

パラメータ一覧は、LKH起動時に表示されます。

下記は、whizzkids96.parを実行した時に表示されるパラメータです。

これをコピペして、パラメータの意味を調べながら書き換えても良いですし、付属のpr2392.parやwhizzkids96.parをベースに編集しても良いと思います。

パラメータの説明は省略します。自分も基本は、まずは動かしてみて、あとはドキュメントを見ながら必要そうなものを追加している感じで使っています。

PARAMETER_FILE = whizzkids96.par
Reading PROBLEM_FILE: "whizzkids96.atsp" ... done
ASCENT_CANDIDATES = 50
BACKBONE_TRIALS = 0
BACKTRACKING = NO
# BWTSP =
# CANDIDATE_FILE =
CANDIDATE_SET_TYPE = ALPHA
# DISTANCE =
DEPOT = 1
# EDGE_FILE =
EXCESS = 0.0322581
EXTERNAL_SALESMEN = 0
EXTRA_CANDIDATES = 0
EXTRA_CANDIDATE_SET_TYPE = QUADRANT
GAIN23 = NO
GAIN_CRITERION = YES
INITIAL_PERIOD = 124
INITIAL_STEP_SIZE = 1
INITIAL_TOUR_ALGORITHM = WALK
# INITIAL_TOUR_FILE =
INITIAL_TOUR_FRACTION = 1.000
# INPUT_TOUR_FILE =
K = 0
KICK_TYPE = 4
KICKS = 1
# MAX_BREADTH =
MAKESPAN = NO
MAX_CANDIDATES = 6
MAX_SWAPS = 0
MAX_TRIALS = 10000
# MERGE_TOUR_FILE =
MOVE_TYPE = 5 SPECIAL
MTSP_MIN_SIZE = 1
MTSP_MAX_SIZE = 247
MTSP_OBJECTIVE = MINMAX
# MTSP_SOLUTION_FILE =
# NONSEQUENTIAL_MOVE_TYPE = 5
OPTIMUM = 1183
# OUTPUT_TOUR_FILE =
PATCHING_A = 1
PATCHING_C = 0
# PI_FILE =
POPMUSIC_INITIAL_TOUR = NO
POPMUSIC_MAX_NEIGHBORS = 5
POPMUSIC_SAMPLE_SIZE = 10
POPMUSIC_SOLUTIONS = 50
POPMUSIC_TRIALS = 1
POPULATION_SIZE = 10
PRECISION = 100
PROBLEM_FILE = whizzkids96.atsp
RECOMBINATION = IPT
RESTRICTED_SEARCH = YES
RUNS = 1
SALESMEN = 4
SCALE = 1
SEED = 1
# SINTEF_SOLUTION_FILE =
STOP_AT_OPTIMUM = YES
SUBGRADIENT = YES
# SUBPROBLEM_SIZE =
# SUBPROBLEM_TOUR_FILE =
SUBSEQUENT_MOVE_TYPE = 5 SPECIAL
SUBSEQUENT_PATCHING = YES
# TIME_LIMIT =
# TOTAL_TIME_LIMIT =
# TOUR_FILE =
TRACE_LEVEL = 1
VEHICLES = 4

プロブレムファイルの書き方

ここでは、２つのパターンでプロブレムファイルの書き方を例示しますが、プロブレムファイルの書き方はサンプルを見ながら学習するのが良いと思います。

公式ページでは、それぞれの問題名がリンクになっていて、それぞれサンプルファイルをダウンロードすることができます。そちらを見ながら、書き方を確認するのが一番早いです。

２次元マップの座標で入力

２次元のマス目上に、点が配置されている場合は、各点の座標を設定したプロブレムファイルを作成します。例えば、下図のように6つの点が指定されている場合、プロブレムファイルは以下のようになります。

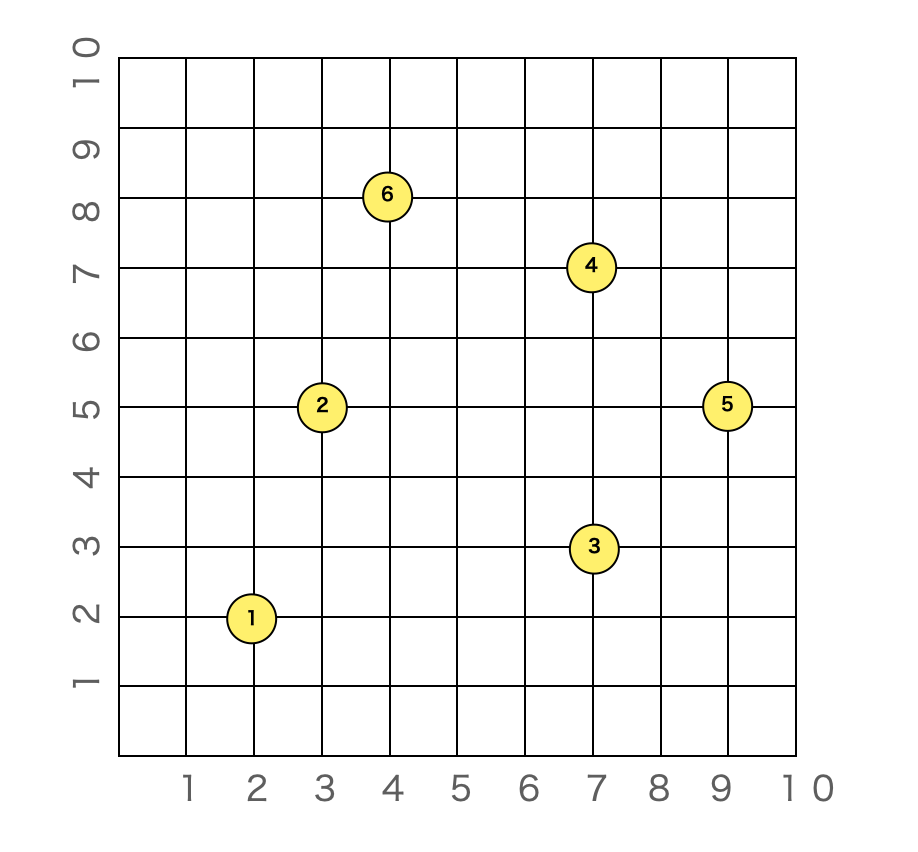
パラメータの説明です。

DIMENSIONは点の数です。EDGE_WEIGHT_TYPEは辺の重みのタイプを指定するもので、２次元の距離なので、EUC_2Dとなります。

最後のNODE_COORD_SECTIONがそれぞれの点の座標で、（点の番号、ｘ座標、ｙ座標）の組みを並べます。

NAME : test001
COMMENT : test001 tsp
TYPE : TSP
DIMENSION : 6
EDGE_WEIGHT_TYPE : EUC_2D
NODE_COORD_SECTION
1 2 2
2 3 5
3 7 3
4 7 7
5 9 5
6 4 6
EOF

次に、パラメータファイルを作成します。とりあえず、pr2392.parをコピーして、必要ない部分をカットし、OUTPUT_TOUR_FILEを追加しました。

OUTPUT_TOUR_FILEを指定しないと結果が出力されません

PROBLEM_FILE = test.tsp
OUTPUT_TOUR_FILE = result.txt
MOVE_TYPE = 5
PATCHING_C = 3
PATCHING_A = 2
RUNS = 10

./LKH test.parで実行すると以下のresult.txtが出力されます。

result.txt

NAME : test001.18.tour
COMMENT : Length = 18
COMMENT : Found by LKH-3 [Keld Helsgaun] Fri Dec 8 14:25:53 2023
TYPE : TOUR
DIMENSION : 6
TOUR_SECTION
1
2
6
4
5
3
-1
EOF

Length=18なので、距離が18のルートを見つけたようです。TOUR-SECTIONが巡回経路で、これを図示すると以下のようになります。

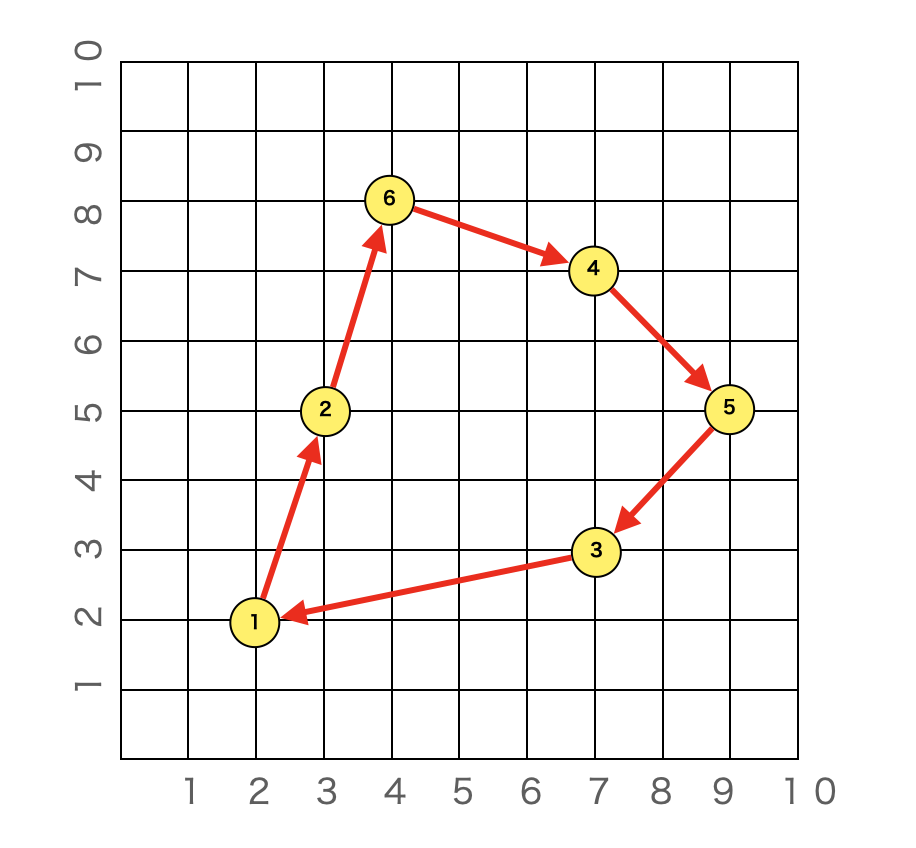
マトリクスで入力

２D上にマップできない問題などは、マトリクスで入力します。ここでは、以下の図の問題を例に説明します。

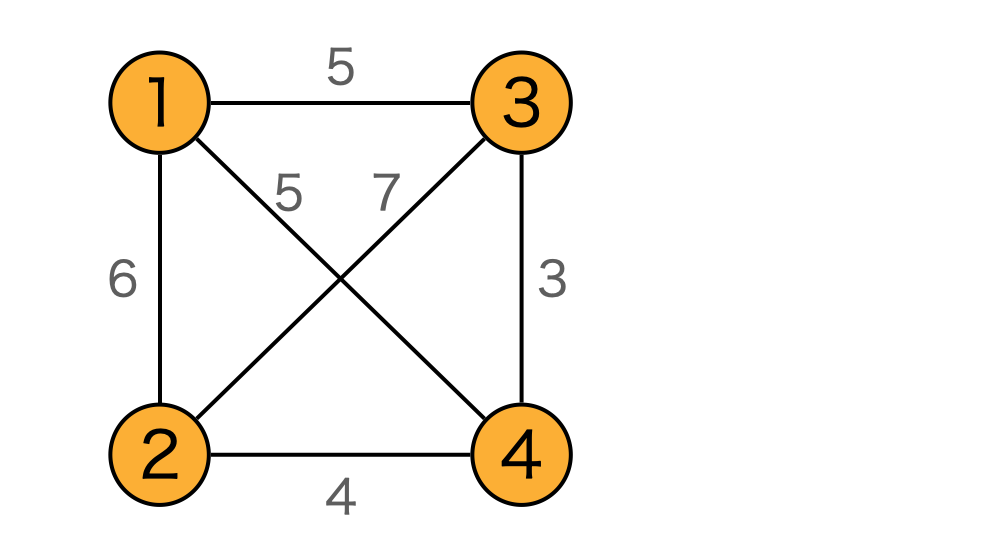
TSP問題２ — 引用元：https://www.msi.co.jp/solution/nuopt/docs/examples/html/02-12-00.html

これを、表にすると以下のようになります。

一行目は、１から１、２、３、４への距離が０、６、５、５であることを表しています。

このような感じで全ての点から点への距離を表にします。

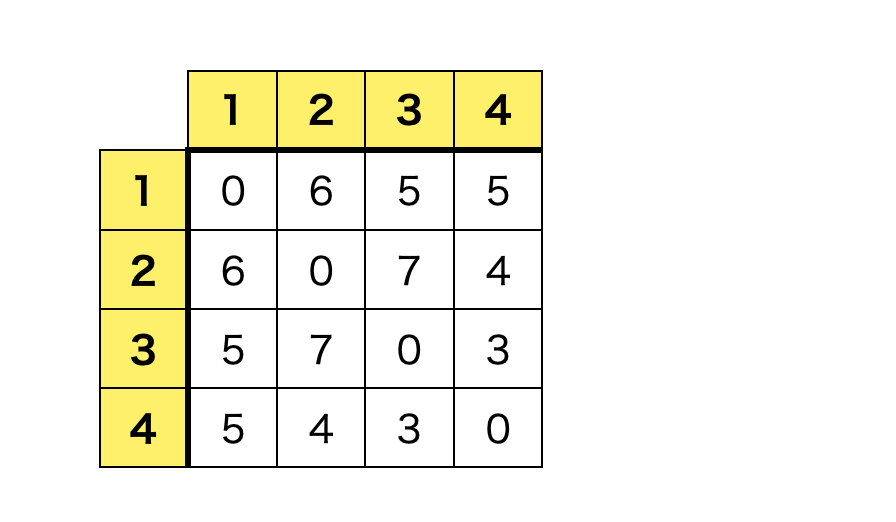
これをプロブレムファイルにすると以下のようになります。

EDGE_WEIGHT_TYPEにEXPLICITを、EDGE_WEIGHT_FORMATにFULL_MATRIXを設定し、EDGE_WEIGHT_SECTIONに、上の表の値を書きます（最後にEOFを入れるのを忘れないように）

点の数が1000などになると、EDGE_WEIGHT_SECTIONがかなり大きくなります。ファイルをプログラムで生成させるなどの工夫をした方がよいです（1000×1000のマトリクスを手動で埋めるのは現実的ではないです）。

ファイルサイズが大きくなって読み込めないかと心配しましたが、数千までは読み込み、実行ができました。

NAME : test002
TYPE : TSP
DIMENSION : 4
EDGE_WEIGHT_TYPE: EXPLICIT
EDGE_WEIGHT_FORMAT: FULL_MATRIX 
EDGE_WEIGHT_SECTION
0 6 5 5
6 0 7 4
5 7 0 3
5 4 3 0
EOF

パラメータファイルも用意します。

PROBLEM_FILE = test2.tsp
OUTPUT_TOUR_FILE = result2.txt
MOVE_TYPE = 5
PATCHING_C = 3
PATCHING_A = 2
RUNS = 10

./LKH test2.parで実行すると以下のresult.txtが出力されます。

result2.txt

NAME : test002.18.tour
COMMENT : Length = 18
COMMENT : Found by LKH-3 [Keld Helsgaun] Fri Dec  8 14:15:28 2023
TYPE : TOUR
DIMENSION : 4
TOUR_SECTION
1
2
4
3
-1
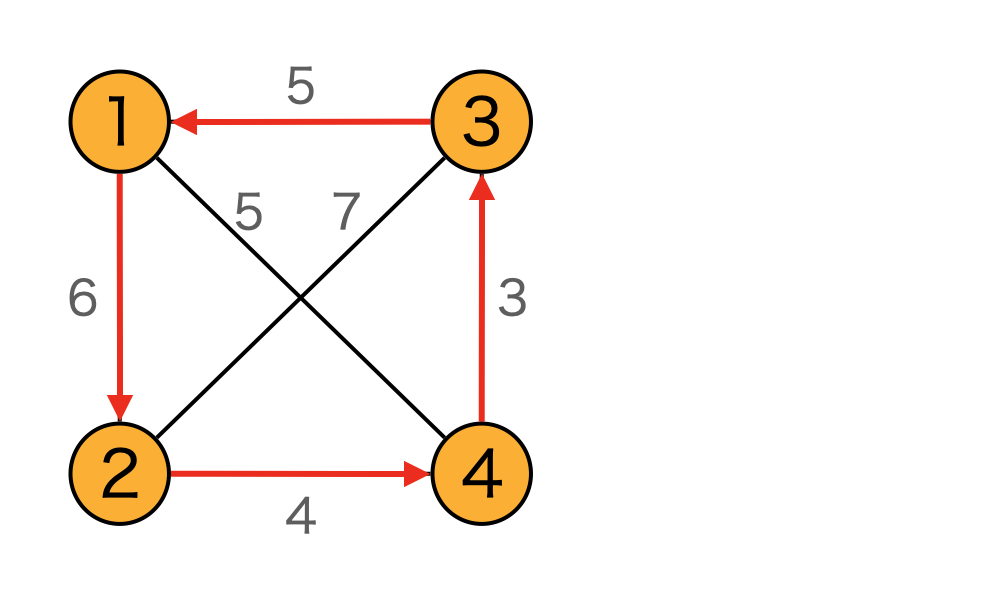
EOF

結果を図に書き込むと以下のようになります。ちなみに、これは最短経路です。

「繋がってない経路は、どう表現するれば良いのか？」

繋がっていないパスは、すごく大きな値を設定してください。例えば1と2の経路がつながっていない場合には、1と2の距離を1000とか、10000とか十分大きな値にしておきます。

その他TIPS

初期ツアーファイルが設定できる

パラメータファイルにINITIAL_TOUR_FILEを設定することで、初期の巡回路を設定することができます。ツアーファイルのフォーマットは、OUTPUT_TOUR_FILEで出力されるファイルと同じフォーマットです。

例えば、以下のようになります。この例では１→２→４→３→１の順番で巡回することを指定しています。

TYPE : TOUR
DIMENSION : 4
TOUR_SECTION
1
2
4
3
-1
EOF

初期の巡回路を設定した方が、収束が早くなったり、最適解に近づいたりします。ある程度効率のよいパスがあらかじめわかっているのであれば、設定しておいても良いです。

まとめ

巡回セールスマンのソルバー、LKHについて解説しました。

このソルバーですが、kaggleのサンタコンペでお世話になっています。年に1回しか使わないので使い方含め毎回調べているので、ブログにまとめてみました。

ソルバーとしてはかなり優秀です。巡回セールスマンの近似解を求めたい場合に活用してみてくはどうでしょうか。

#LKH-3 #TSP #巡回セールスマン問題