【Python】deep-translatorを使ってcsvファイルのテキストを翻訳する方法
tadanori
Aru's テクログ（Aruaru0）
3000万の資産で何年暮らせるかを、モンテカルロ法で求めてみる【Python】
tadanori
モンテカルロ法という数値シミュレーション手法があります。ベイズモデリングや金融市場の未来予測などで使われている手法ですが、ここではこれを使って「リターンr%の資産X万円をY万円ずつ切り崩したら何年暮らせるか」をこの手法を使って計算してみました。
こういうのが、「ファイナンス✖️IT」かなーとか思ったりします
資産寿命電卓はこちら
JavaScriptで記述した資産寿命電卓は以下の記事あります。金額を設定してシミュレーションできます。
モンテカルロ法
モンテカルロ法とは
モンテカルロ法は、数値シミュレーションの手法の１つです。
確率分布を使ってランダムな値を生成し、その結果を解析することで、問題の近似値を求めることができます。
ランダムな値を生成して、シミュレーションを繰り返す必要があるため、PCの性能が低かった頃は単純なシミュレーションにしか使えなかったのですが、PCの性能が向上してかなり複雑な問題にも使えるようになりました。
ベイズモデリングで使われるMCMC(マルコフ連鎖モンテカルロ法）なんかは、PCの演算性能があって初めて実用的になったと感じてています。
モンテカルロ法を使うと、複雑な問題や確率要素を含む問題の近似解を求めることができるため、金融市場の未来予測などに利用されています。
この記事では、「資産の取り崩し」をモンテカルロ法を使って考えてみます。
せっかく、ファイナンシャル・プランナー＆IT技術者なので、こういう題材もたまにはよいかなと思いました。
円周率を求める
モンテカルロ法の説明として、円周率を求める問題を解いてみます。
モンテカルロ法で解く場合は、以下のような手順になります。
- [0, 1]の範囲の一様乱数をx,yの２つ生成する
- これが円の中に含まれるかどうか調べる。含まれる場合はcnt+1する
半径r=1.0の円で考えると$x^2 + y^2 \leq 1$かどうかを調べればOKです。 - ①〜②をn回繰り返す
- 半径を$r$とすると、円の面積は$\pi r^2$ 。矩形の面積は$(2r)^2=4r^2$で、$\pi = 4\frac{円の面積}{矩形の面積}=4\frac{\pi r^2}{4r^2}=\pi$となる。なので、$4cnt/n$が円周率
モンテカルロ法の説明では、円周率の計算を使うことが多いです
以下がコードです。コードでは、N=100,1000,10000, 100000, 1000000, 10000000と試行回数を変えて（シミュレーション回数を変えて）円周率を求めています。
import random
N = [100, 1000, 10000, 10**5, 10**6, 10**7]
for n in N:
cnt = 0
for i in range(n):
x, y = random.random(), random.random()
if x**2 + y**2 <= 1:
cnt += 1
pi = 4 * cnt / n
print(f"n = {n} pi={pi}")結果は、以下のようになります。試行回数を増やせば3.14…に近づいていることがわかります。
実行結果
n = 100 pi=2.72
n = 1000 pi=3.128
n = 10000 pi=3.1164
n = 100000 pi=3.15172
n = 1000000 pi=3.141332
n = 10000000 pi=3.1406916
資産の取り崩し戦略
モンテカルロ法を使って、資産の取り崩しをシミュレーションしてみます。
概要
今回、ターゲットとする問題は、以下になります。
資産取り崩しの問題
X万円をリターンr%、リスクe%の商品で運用しながら、毎年Y万円取り崩すと、何年くらいで資産が尽きるか
リスクを考慮しないものは、資本回収係数を使って計算できます
資本回収係数は、n年で取り崩す場合いくらずつ取り崩せるかを計算するので少し違います。詳しくは、以下を参照してくだい
リスクを考慮した場合も、数値計算で求めることはできないことはないですが、「０円になったらそこで打ち切る」ことを考慮すると少し複雑になります。
このような問題は、モンテカルロ法が向いた問題だと思います。
以下、この問題をモンテカルロ法を使って解いてみます。
いざ、シミュレーション
１回シミュレーションする関数を作成
まずは、シミュレーションを1回だけ行う関数を作成します。関数は以下になります。
import random
def simulate(amount, cash, ret, risk, nmax = 100) :
cnt = 0
ret /= 100
risk /= 100
p = []
for i in range(nmax): # 最大年数繰り返す
r = random.normalvariate(ret, risk) # 平均rate, 偏差rateの正規分布の乱数を生成
amount *= (1 + r) # 今年の総資産額を計算
amount -= cash # 毎年の取り崩し額を引く
cnt += 1
if amount <= 0: break # もし、総額が0になったら終了
p.append(amount)
return cnt, p # 総額とシミュレーション結果を返す引数の意味は以下の通り
- amount … 最初の資産額
- cash … 毎年引き出す額
- ret … リターン（％）
- risk … リスク（％）
- nmax … 打ち切る年数（デフォルト100年）
処理の中身は以下のようになります。
r = random.normalvariate(ret, risk)で、平均ret, 偏差riskの正規分布に基づく乱数を計算- 今年の総資産額を計算
- 取り崩し分を引く
- 総額が０以下になったら終了
- 打ち切り年数になったら終了
- 年数を返す
内容自体はそれほど難しくないと思います。この関数を1回呼び出すと、乱数を使ったシミュレーションが1回実行され、継続年数が返されます。
毎年のリターンはランダムウオークだとしてシミュレーションしています。ここも色々条件をつけることができます。例えば、シミュレーション結果でリスクとリターンを修正するなども可能です。
どこまでやっても想定に基づいたシミュレーションなので、どこまで複雑にするかは、趣味に近い部分がありますね。
モンテカルロ法
モンテカルロ法では、simulate関数を複数回呼び出してシミュレーションを繰り返します。
以下は、「資産5000万円、取り崩し200万円、リターン3%, リスク3%」という条件で、1000回シミュレーションを繰り返した例です。
x = []
random.seed(42)
for i in range(1000) :
cnt, p = simulate(5000, 200, 3, 3)
plt.plot(p, linewidth=1)
x.append(cnt)
plt.show()
plt.hist(x, bins=[i for i in range(1, 101)])
plt.show()
y = [sum(x[:i])/i for i in range(1, len(x))]
plt.plot(y)
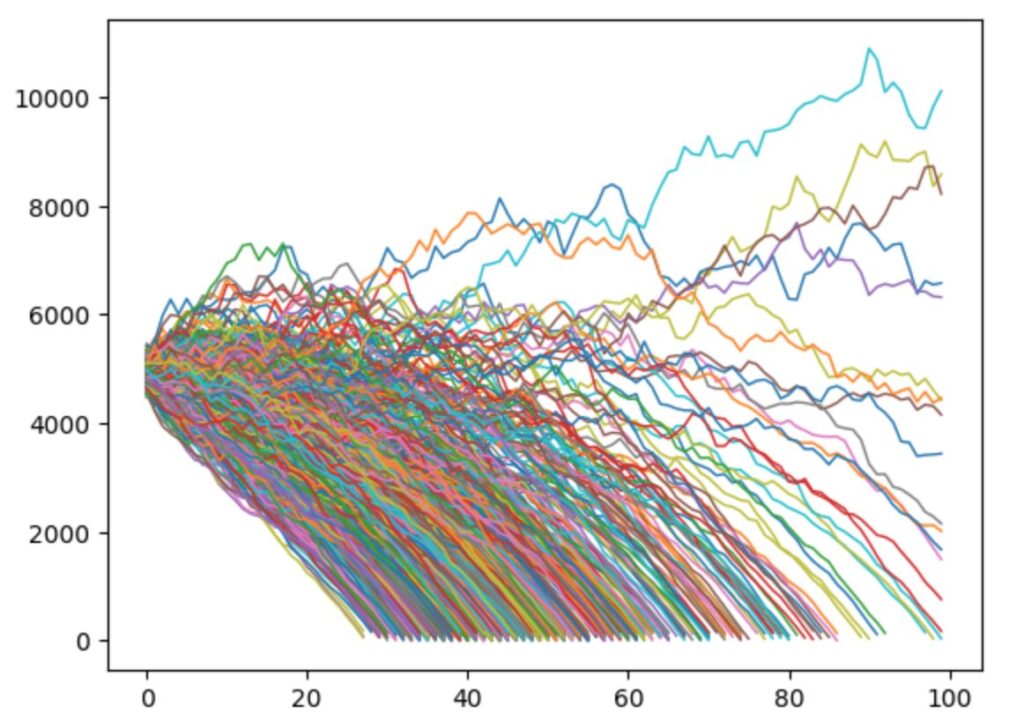
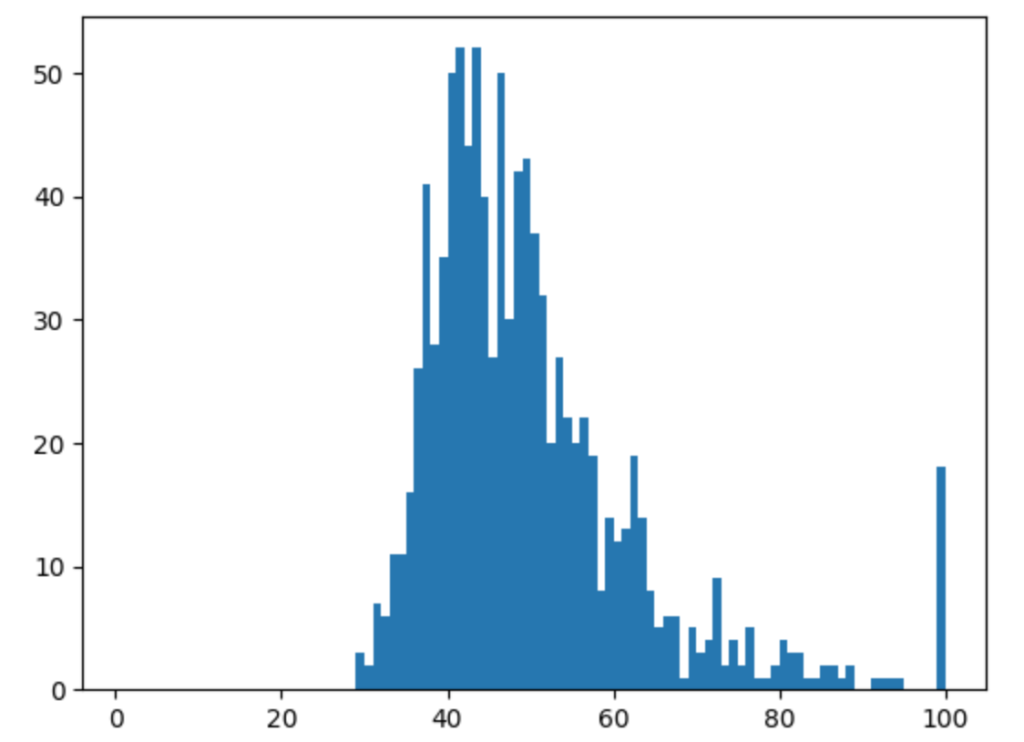
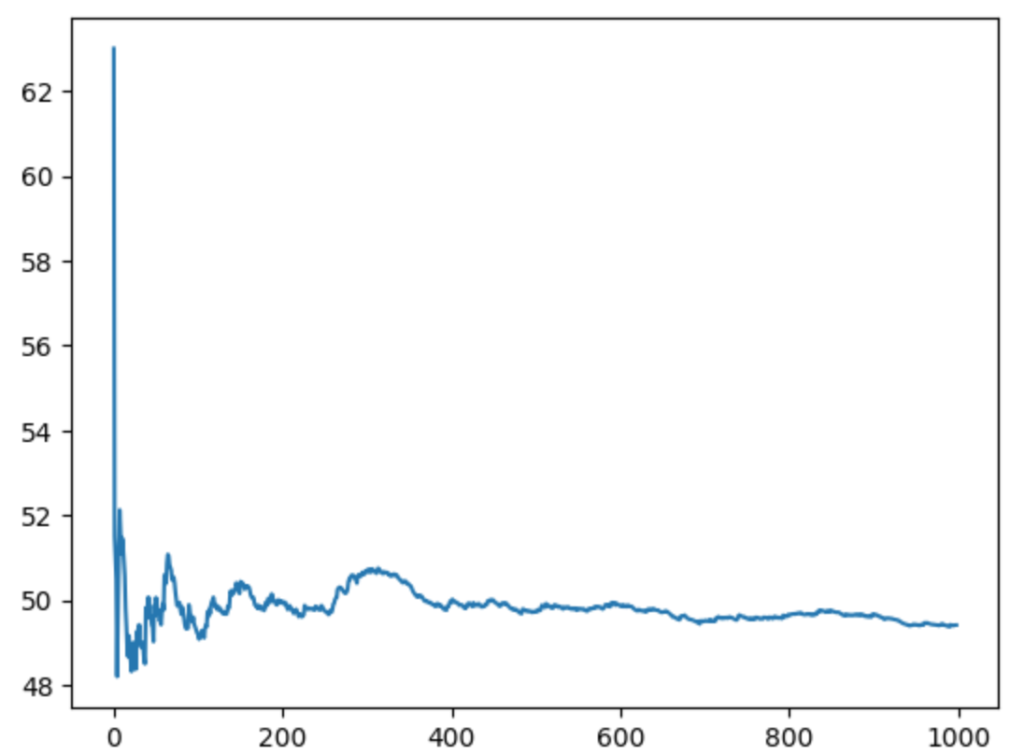
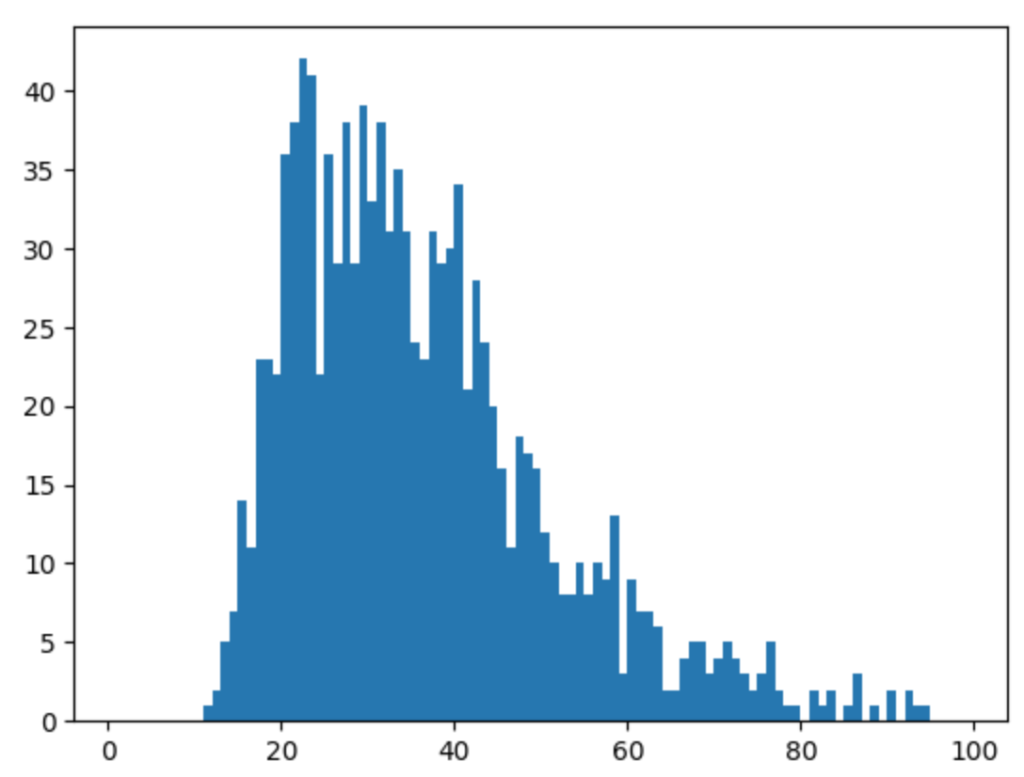
plt.show()以下の３つは、結果のグラフです。
左のグラフは、各シミュレーションの結果で横軸が年数、縦軸が資産の残りです。これが０になっている年まで資産がなくならなかったことになります。
真ん中んグラフは、資産が維持できた年数をヒストグラムで示したものです。平均で40〜50年くらいの年数、資産が維持できたことになります。
右のグラフは、シミュレーション回数（横軸）と、平均年数（縦軸）のグラフです。試行回数を重ねると収束していることがわかります。
モンテカルロ法を使うと、このような問題の結果を求めることが可能です。
今回のモデルは、「現在の資産額だけで翌年の資産額が決まる」というマルコフ課程に基づくものなので、MCMC的なシミュレーションになります。
結果
このモデルを使って、少し現実的なシミュレーションを行ってみます。
シミュレーションする内容は、以下の通りです。
資産3000万円で毎年300万円ずつ取り崩す、資産はS&P500に全て投資している。資産がなくなるまでの年数を調べる
S&P500のリスクとリターンは、期間などによって違いますが、今回はリターン11.5%, リスク18.1%という数値を使います。
シミュレーションは過去の実績に基づくので、将来を保証するわけではないですが、大体のイメージを掴むのには十分だと思います
コードは以下になります。
# 3000万円で米国株only 300万円取り崩し
x = []
for i in range(100000) :
cnt, p = simulate(3000, 300, 11.5, 18.1)
x.append(cnt)
plt.show()
plt.hist(x, bins=[i for i in range(1, 101)])
plt.show()
plt.hist(x, bins=[i for i in range(1, 100)])
plt.show()
plt.boxplot(x)
plt.show()
print("平均", np.mean(x))
print("中央値", np.median(x))
# 75パーセント点、25パーセント点を取得
q75, q25 = np.percentile(x, [75 ,25])
iqr = q75 - q25
print("最短", min(x))
print("最長", max(x))
print("25パーセント点", q25)
print("75パーセント点", q75)シミュレーションは、10万回行いました。
図は左から、ヒストグラム、100年を除いたヒストグラム、年数の分布を示す箱ひげ図です。
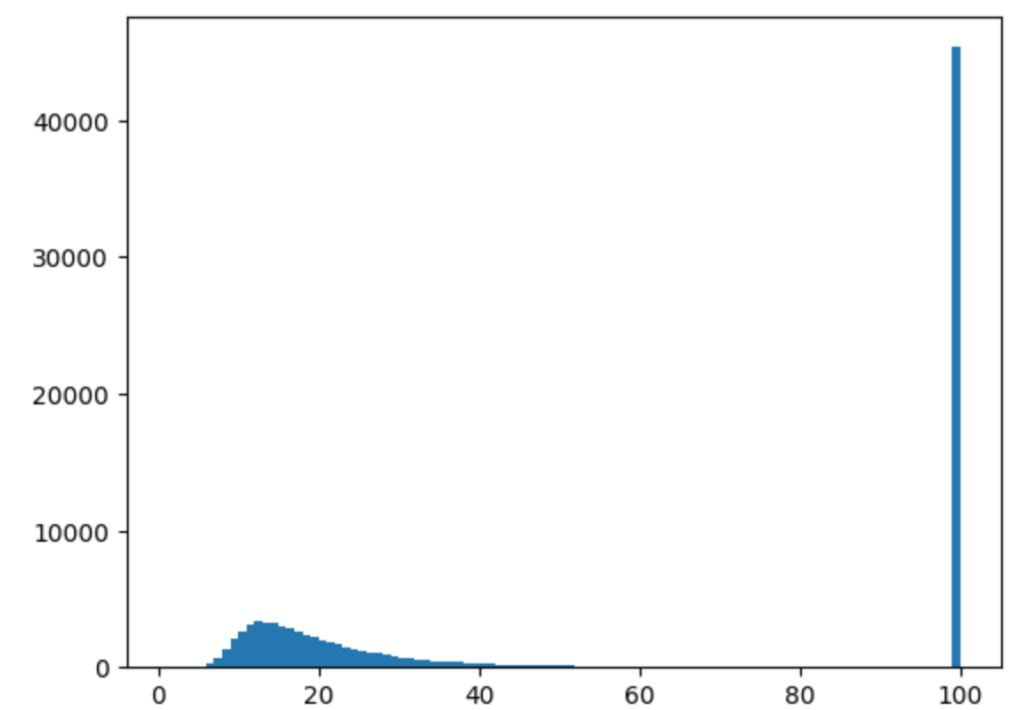
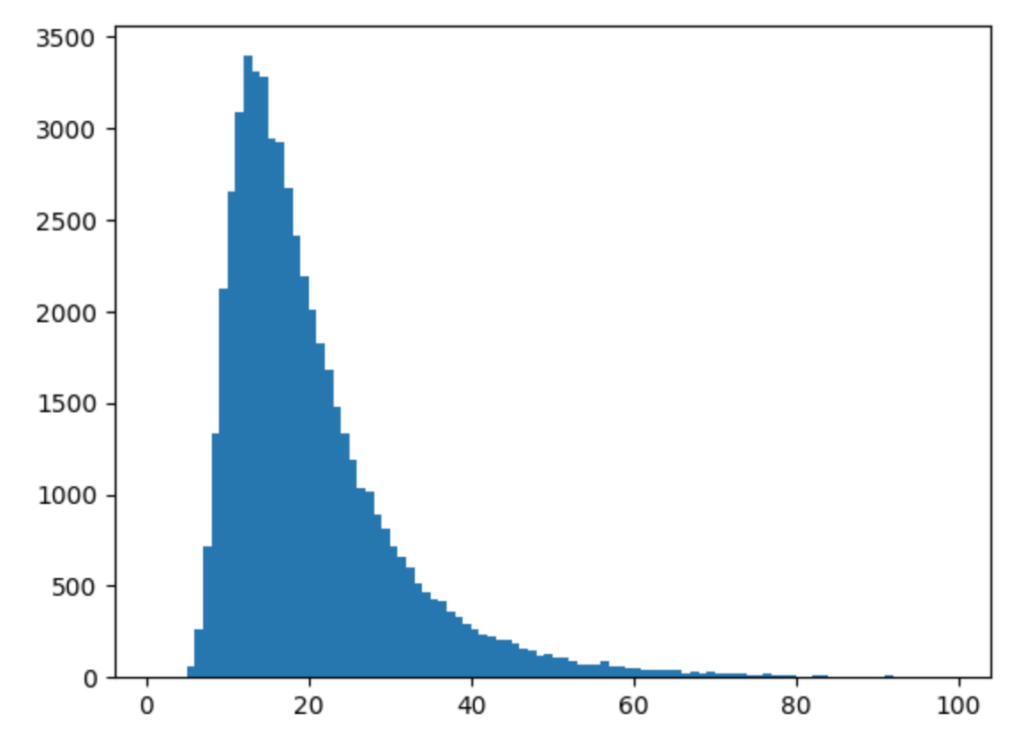
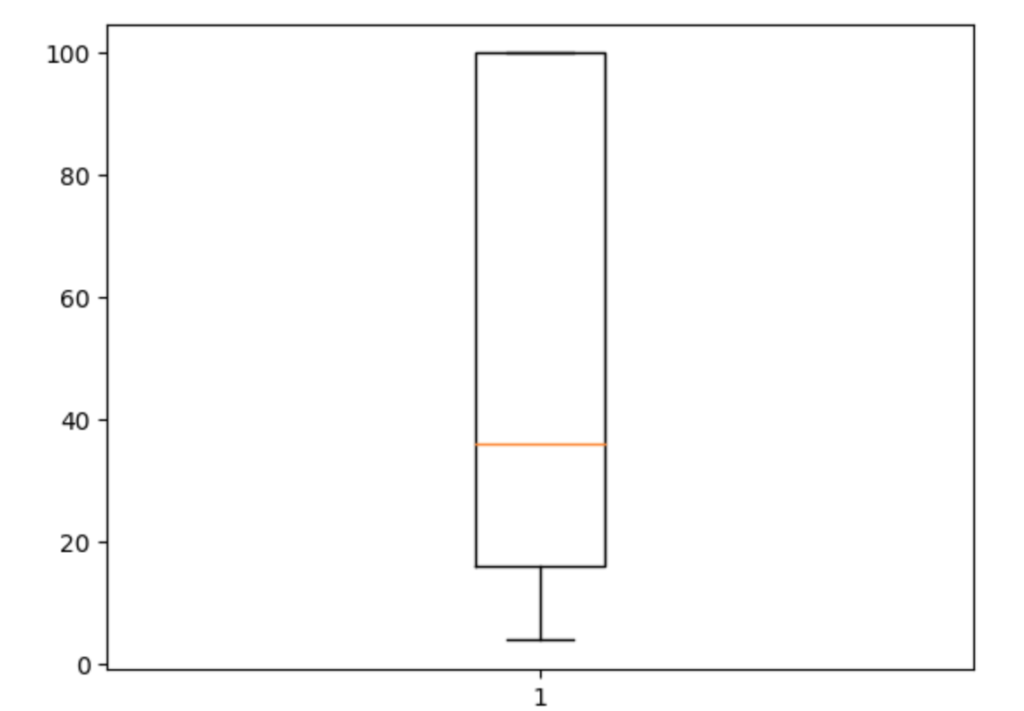
利息がなければ3000万は300万ずつ切り崩せば10年で無くなりますが、リターン11.5%, リスク18.1%なら平均で56年、中央値で36年は資産で生活できるようです。
ただ、シミュレーションの結果では、最悪で4年で資産が0になります。これが投資によるリスクになります。
また、50%の確率で16年〜100年の間は生活可能だということがわかります。
平均 56.25822
中央値 36.0
最短 4
最長 100
25パーセント点 16.0
75パーセント点 100.0あくまでも、S&P500のリスクとリターンが前提通りでの結果ですが、このようなリスク込みの予測が簡単にできるのがモンテカルロ法の利点です。
ちなみに、資産を１億円でシミュレーションした場合は以下になります。
平均値99年、中央値100年、75%は100年間以上資産が残る計算になります。
FIREする場合目標が1億円な理由がなんとなくわかる結果になりました。
ただ、10万回のシミュレーションでは、最短で11年で資産が尽きるパターンがありました。10万回に1回は1億円あっても10年くらいで資産が尽きることがあるようです。
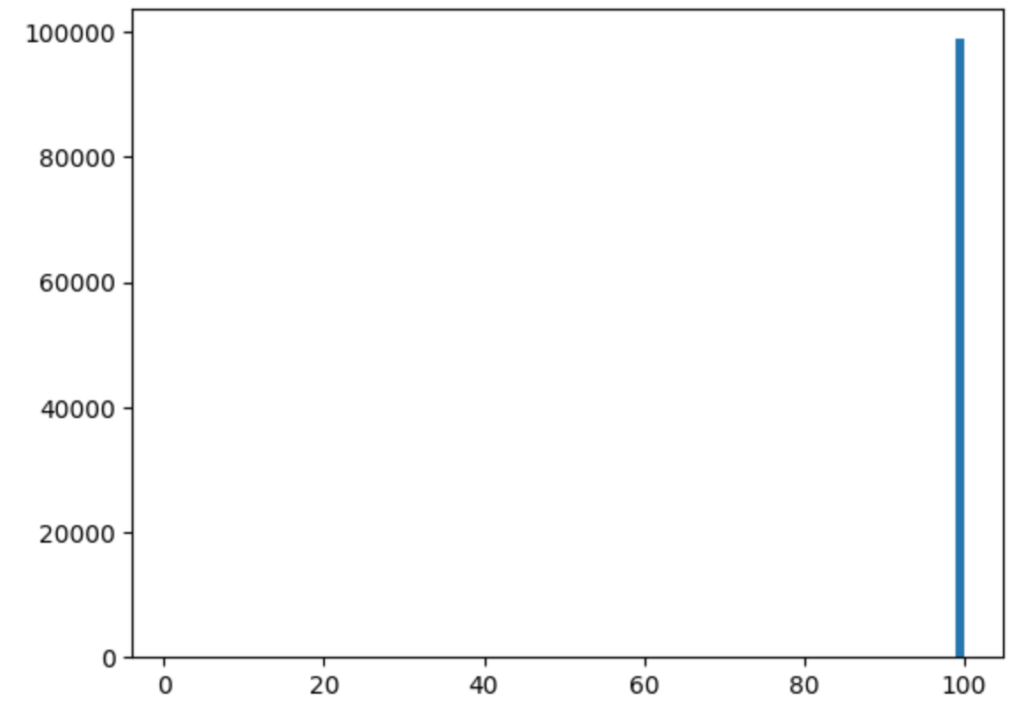
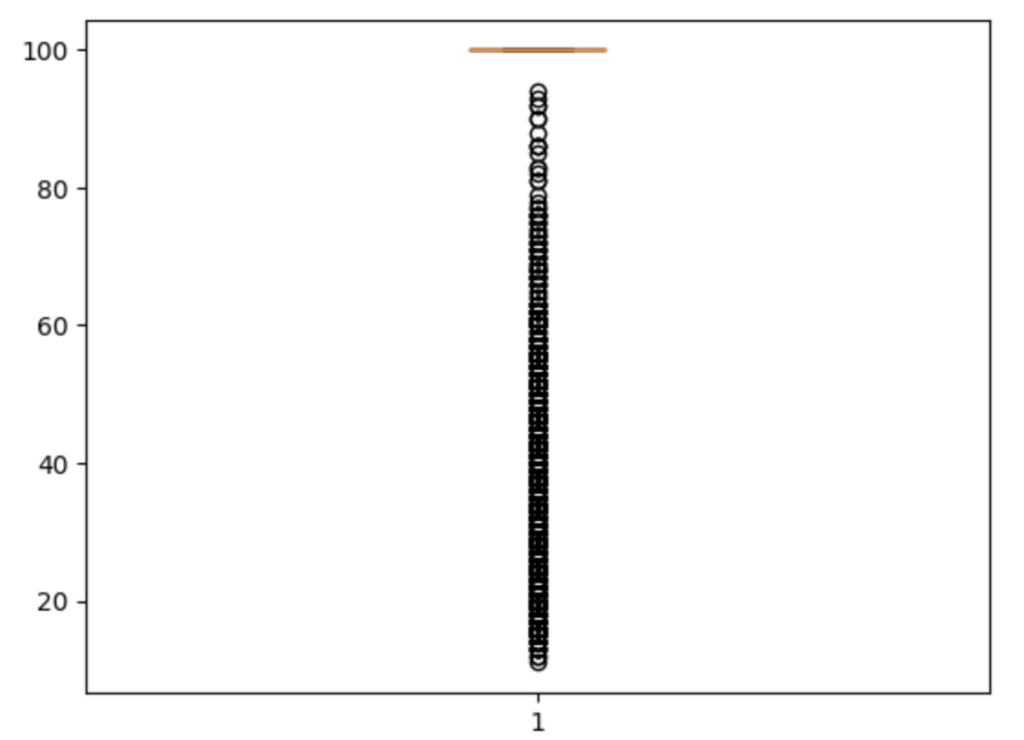
平均 99.25995
中央値 100.0
最短 11
最長 100
25パーセント点 100.0
75パーセント点 100.0１億円の資産の場合に、100年持たない割合も計算してみました。100年も資産が持たない比率はわずか1.2%です。
まとめ
モンテカルロ法を使って、資産の取り崩しをシミュレーションしてみました。モンテカルロ法の場合、「毎年の取り崩し額にインフレ分を加味する」とか、「年金がもらえるようになる年齢から取り崩し額を減らす」などを加味した計算を簡単に行うことができます。
ある程度までは、数式をたてて求めることができますが、複雑な条件を入れる場合はモンテカルロ法は良い選択肢だと思います。
