数列問題｜足して１００以上のパターン数を高速に数える方法（AtCoder向け）

tadanori

この記事では、A1, A2, A3…Anという数列の２つを足して100以上になるパターン数を高速に数える方法を考えます。ここではPythonで問題を解いてみます。

Contents

対象問題
愚直解
高速化した解法
- 解法①
- 解法②
まとめ

対象問題

対象とする問題は以下になります。

n個の数列$A_1, A_2, A_3…A_n$の2つの要素を足して100以上になる組み合わせの数はいくつありますか？

愚直解

愚直解は２重ループを使って以下のように記述できると思います。

下記のプログラムでは、n=10とし、1から100の乱数を発生させて数列aを生成し、100以上かどうかを判定し100以上であればcntをインクリメントします。

import random

n = 10
a = [random.randint(1, 100) for i in range(n)]

print(a)
cnt = 0
for i in range(n):
    for j in range(i+1, n):
        print(a[i], a[j], end=" ")
        if a[i] + a[j] >= 100 :
            cnt+=1
            print(">=100", "cnt=", cnt)
        else :
            print("")
print(cnt)

プログラムでは途中経過も同時に出力するようにしていますが、結果は例えば以下のようになります。

[14, 25, 54, 21, 90, 21, 15, 17, 39, 75]
14 25 
14 54 
14 21 
14 90 >=100 cnt= 1
14 21 
14 15 
14 17 
14 39 
14 75 
25 54 
25 21 
25 90 >=100 cnt= 2
25 21 
25 15 
25 17 
25 39 
25 75 >=100 cnt= 3
54 21 
54 90 >=100 cnt= 4
54 21 
54 15 
54 17 
54 39 
54 75 >=100 cnt= 5
21 90 >=100 cnt= 6
21 21 
21 15 
21 17 
21 39 
21 75 
90 21 >=100 cnt= 7
90 15 >=100 cnt= 8
90 17 >=100 cnt= 9
90 39 >=100 cnt= 10
90 75 >=100 cnt= 11
21 15 
21 17 
21 39 
21 75 
15 17 
15 39 
15 75 
17 39 
17 75 
39 75 >=100 cnt= 12
12

上記の数列[14, 25, 54, 21, 90, 21, 15, 17, 39, 75]の場合は、100を超える組み合わせは12個になります。

愚直解は２重ループになっているので、計算量は$O(N^2)$となります。

高速化した解法

解法①

高速化するには、ループ数を減らす必要があります。

数列の２つの組み合わせだけに注目した場合、数列をソートしても結果は変わりません（組み合わせパターンの数は変化しない）。

なので、ソートして考えます。

現在注目するAを$A_i$、比較するAを$A_r$とします。$r$の初期値は一番大きな値にセットします。次に、A[i] + A[r]が100未満になるまでrを小さい方に移動させます。

するとN-(r+1)が、$A_i$と加算すると100を超える数になります。

これをiが0からn-1まで繰り返せば、個数がわかります。

なお、rは初期化せずにそのまま続けることができます（i+1の要素はiより常に大きいのでrより右側とは足して100になる）。

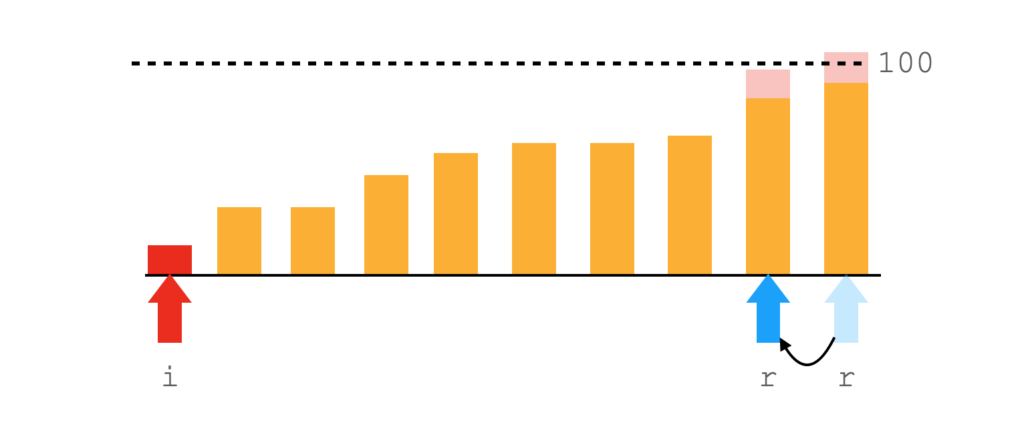
注意点としてはrがiより小さくならないようにすることです（プログラム中のmax(i, r)）。

これで計算量$O(n)$で個数を数えることができます。

import random

n = 10
a = [random.randint(1, 100) for i in range(n)]
a.sort()

r = n-1
tot = 0
for i in range(n) :
    while (r >= 0 and a[i] + a[r] >= 100) :
        r -= 1
    r = max(i, r)
    tot += n - (r + 1)

print(tot)

解法②

考え方は同じで、「ソートして、足して100以上になる要素の場所を調べ、右側にある要素数をカウント」します。

違うのは、要素の数を調べる部分です。

こちらの方法では、100以上となる境界を二分探索で求めます（bisectを利用）。

この解法の計算量は$O(nlogn)$になります。

import bisect
import random

n = 10
a = [random.randint(1, 100) for i in range(n)]
a.sort()

tot = 0
for i in range(n):
    target = 100 - a[i]
    pos = bisect.bisect_left(a, target, i + 1)
    tot += n - pos

print(tot)