木構造のグラフの重心を簡単に求める方法｜Pythonによるアルゴリズム解説

この記事では、木構造のグラフの重心を求める方法について解説します。考え方さえ知っていれば、木の重心はDFSを使って簡単に求めることが可能です。ここではPythonコードを使いながらアルゴリズムについて解説します。

木の重心の求め方

グラフが木構造の場合、全てのノードが連結で閉路（cycle）を持たないグラフとなります。閉路とは名前の通り、辺をたどって元のノードに戻ってくるサイクルです。

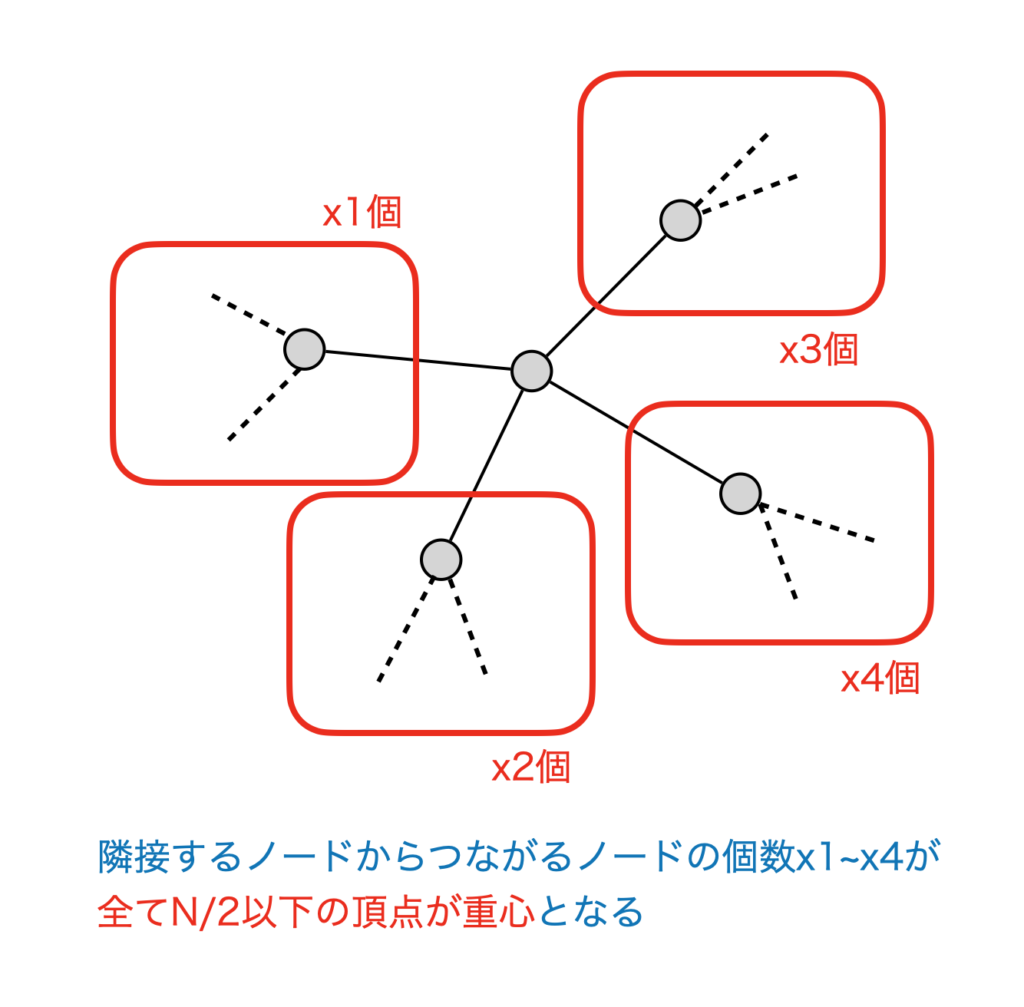
木の重心となる点は、「隣接するノードからつながるノードの個数が、全てN/2以下となる頂点」です。また、隣接するノードからつながるノードの個数がN/2より大きい場合、重心はN/2より大きい方に含まれるノードのいずれかとなります。

逆に考えると、ある方向にN/2を超えるノードが繋がっている場合、そのノードは重心ではありません（ある方向に半数を超えるノードがある＝重心ではないから）。そのようなノードを除外していくと、結果的に重心候補は１つまたは２つになります。

下の図は、ある頂点に隣接するノードの子ノードの数をx1, x2, x3, x4とした場合の略図です。もし、x1~x4がすべてN/2個以下であれば、このノードは重心となります。

これを求める方法はいろいろあると思いますが、今回は深さ優先探索をにより求める方法を取りたいと思います。

Pythonプログラム

以下、Pythonプログラムです。

dfs()の部分が、重心を求める部分になります。重心はcentroidにリストとして格納されます
※頂点数が偶数か奇数かにより、重心となる頂点は１つまたは２つとなります

import sys
sys.setrecursionlimit(10**6)

n = int(input())

node = [[] for _ in range(n)]
for e in range(n-1):
    a, b = map(int, input().split())
    a-=1
    b-=1
    node[a].append(b)
    node[b].append(a)


size = [0 for _ in range(n)]
centroid = []

def dfs(cur, prev):
    size[cur] = 1
    mx = 0
    for e in node[cur] :
        if e == prev : continue
        size[cur] += dfs(e, cur)
        mx = max(mx, size[e])
    mx = max(mx, n - size[cur])
    # 一番頂点数の多い枝の数がn/2を超えていないノードは重心として追加
    if mx*2 <= n : centroid.append(cur)

    return size[cur]

dfs(0, -1)

print(centroid) # 木の重心（1 or 2個）

プログラムの構造としては、以下のような子ノードの頂点数を調べるDFS（深さ優先探索）のプログラムを少しただけ変更したものになります。具体的には、一番大きな子ノード数を持つ枝のノード数をmxに格納するように変更するだけです。

あとは、最大の子ノードを持つ枝のノード数がmx*2以下（＝半数以下）であれば、重心点のリストに追加しています。

def dfs(cur, prev):
    size[cur] = 1
    for e in node[cur] :
        if e == prev : continue
        size[cur] += dfs(e, cur)
    return size[cur]

以上、深さ優先探索（DFS）を行うだけで、重心を求めることが可能です。

実際に以下のようなデータで実験してみます。

test.txtの意味は、一行目が頂点数n、残りがノードa, bが辺で接続されていることを示します。辺の数は、木なので頂点数-1となります。

10
1 2
1 3
2 4
2 7
4 5
4 6
6 8
6 9
7 10

上記を図示したものが以下になります。重心は頂点2または4のどちらかになります。

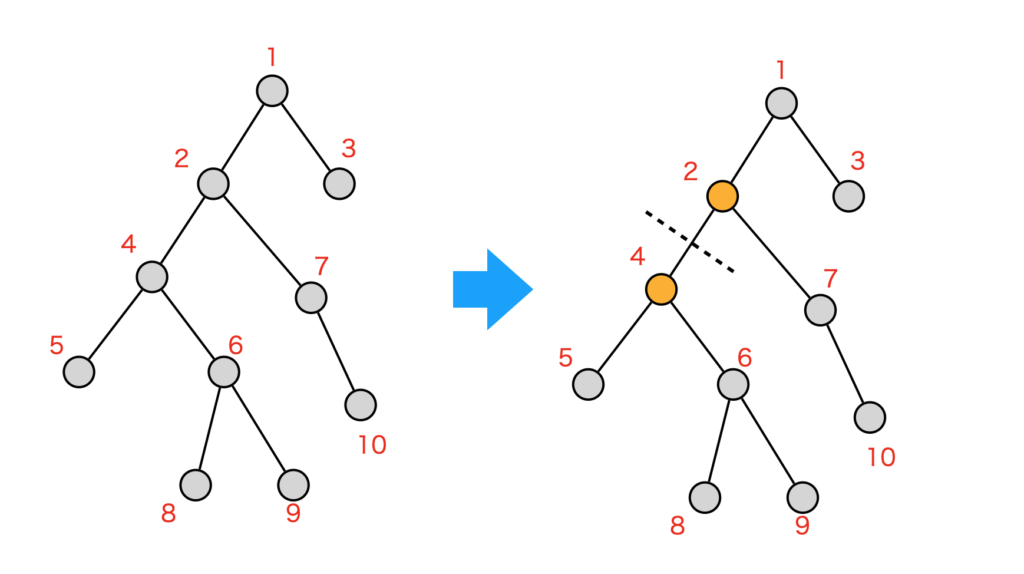
プログラムを実行すると、[3, 1]と出力されます（プログラムでは、頂点を0番から始まるようにしているので、3→頂点4, 1→頂点2のことになります）。

以上のように、比較的簡単なプログラムで重心を求めることができました。

まとめ

木の重心を求める方法についてPythonプログラムを作成してみました。AtCoderのABC362のF問題を解くときに、サクッと実装できなかったですが知っていれば簡単でした。わかってしまうと、何を悩んでいたのだろうと思ってしまいます。

ある/Aru

IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)

XContact

専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中