AtCoderで役立つ記事一覧（Python, Go言語）
Aru
Aru's テクログ（Aruaru0）
プログラミングで間違えやすい、植木算の計算方法を解説
Aru
植木算は、プログラム時にミスが多い計算です。植木算のミスは、実行結果としては演算誤差のように見えることが多く、結合後は見つけにくいバグです。この記事では、植木算の落とし穴と注意点について解説します。
植木算とは
植木算とは、算数の問題の１つで、等間隔に並んだ植木の数や間隔を数える問題です。
この問題のポイントは、植木は両端に存在していることです。
例えば、5本の植木が100ｍの区間に等間隔に並んでいる場合、植木と植木の間は４つです。なので、植木の間隔は25ｍとなります。100÷5=20ｍでない点がポイントです。
「こんなの間違わない」と思うかもしれませんが、プログラミングを行う場合などに結構ミスをする部分だったりします。
この記事では、植木算のルールと、植木算の応用問題をいくつかあげて解説したいと思います。
画素値計算を例にあげると、一般的に画素値は0~255の値の256通りの値で表現します。これを0~1の浮動小数に変換する場合に、「画素値は256通りなので画素値のステップは1÷256」と考えて計算してしまうと、最大画素値は255*1/256となり1.0になりません。これが勘違いによるバグです。
「大した差じゃない」と思われるかもしれませんが、この差は画像で見えることがあります。このような勘違いによるバグは、いろんなとこで発生するので注意が必要です。
植木算のルール
一列に並んでいる場合
一列に８本の木が並んでいる例です。
図でみると一目瞭然ですが、８本の木の間は７つです。
一般化すると「n本の木の間の区間はn-1」となります。
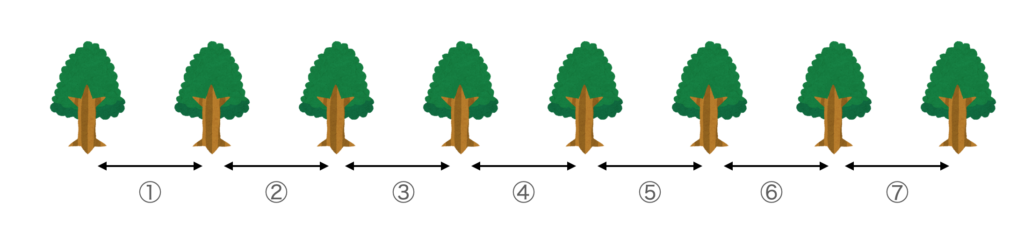
木の数がn本の場合、区間の数はn-1という点を忘れて、区間数をnで計算してしまうのが、最も多いミスです。
円形に並んでいる場合
例えば、湖の周りに木を植える場合などには注意が必要です。この場合は、８本の木を植える場合、木と木の間も8になります。
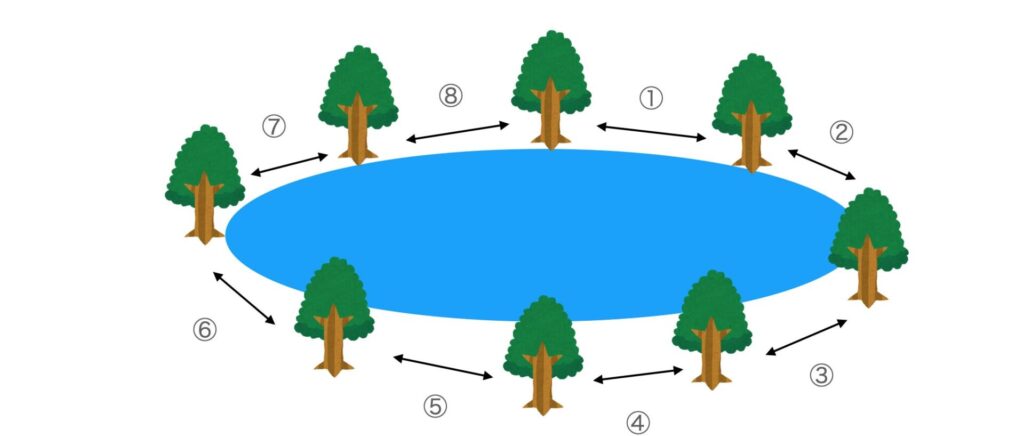
円形に並んでいる場合は、n-1にはならないことに注意してください。
円形に並んでいる場合にも植木算の計算を適用しないように注意です
円形に並んでいる場合で、スタートとゴールが同じという場合も注意です。この場合は木自体が-1です。
植木算の問題例
基礎問題
問題
ある公園の歩道に沿って等間隔に街路樹を植えました。両端に街路樹があるとして、10メートルごとに街路樹を植えた場合、全体の距離が90メートルになるようにするためには、何本の街路樹が必要でしょうか？
街路樹の本数をnとおきます。10メートル毎に街路樹を植えて間隔が90メートルになるので、植木算では間隔がn-1となることを考えると以下の式になります。
$$
\begin{align}
(n-1)\times 10& = 90\\
n-1 &= \frac{90}{10} = 9\\
n &= 9 + 1 = 10\\
\end{align}
$$
これを解くと、$n=10$になります。図で書くと以下のようになります。
応用問題
問題
長方形の庭の周囲に等間隔でフェンスの支柱を立てたいと考えています。庭の長辺は30メートル、短辺は20メートルです。支柱は角を含むすべての辺に立てるものとし、各支柱の間隔を5メートルとします。支柱の総数を求めなさい。
先ほどの問題と同様に考えると、長辺には$30/5+1=7$本、短辺には$20/4+1=5$本の支柱が必要なおことがわかります。
ただ、短辺と長辺で角の４本は重複しています。なので、以下のように重複して計算される４本を引く必要があります。
$$
7本 \times 2 + 5本 \times 2 – 4本 = 20本
$$
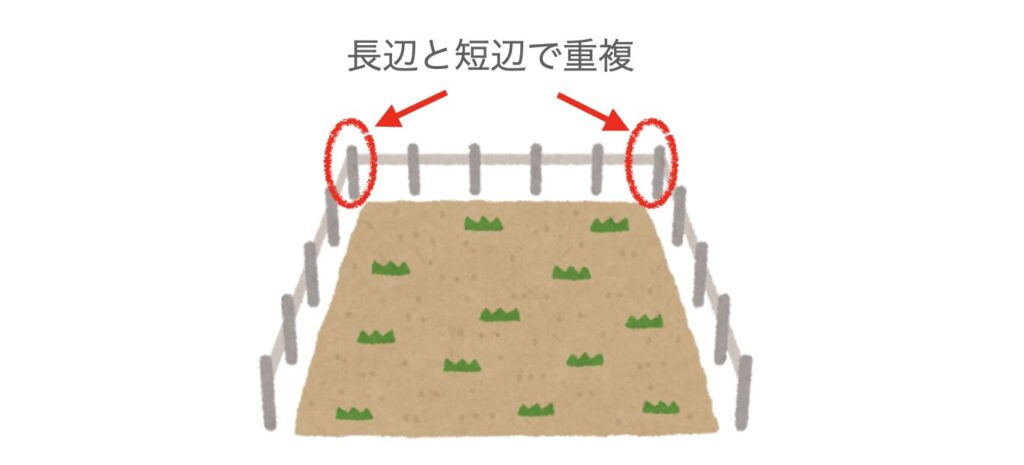
この問題は、植木算に加えて重複する部分を考慮する問題になります。
まとめ
この記事では、植木算について解説しました。こんなの間違わないと思う人も多いと思いますが、プログラミングする時にうっかりミスが多い部分でもあります。植木算には気をつけましょう。
ABOUT ME
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
