Pythonで正規分布のグラフを描く方法｜綺麗なベルカーブを描く

Aru

Pythonで正規分布のグラフを描画する方法を解説します。書きたいのは以下のよう$\mu=0.0, \sigma=1.0$のベルカーブのグラフです。

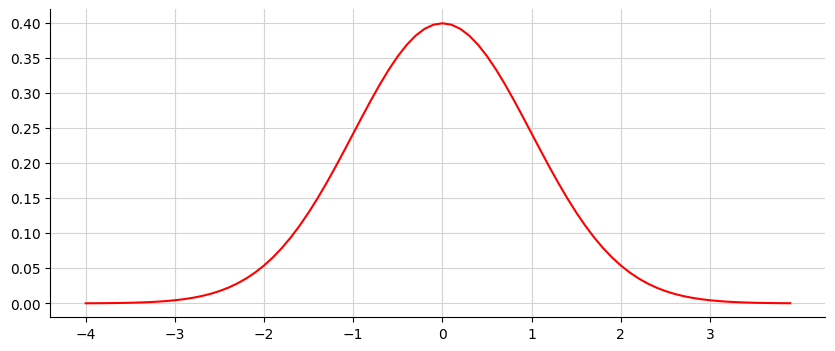
このグラフは資料に貼り付けるために作成しました。この手のグラフはWebでたくさん見つけることができますが、著作権を考えると自分の資料へのコピペは要注意です。そこで、ベルカーブを自作するためのPythonコードを作成し、描画しました。

なお、上記グラフは自由にコピペしてもらってOKです

こんなの需要あるかわかりませんが、とりあえず

Contents

正規分布とは
グラフを書く
まとめ

正規分布とは

確率・統計を学習している方には、お馴染みの正規分布の確率密度関数です。

$
f(x) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp\biggl(-\frac{(x-\mu)^2}{2\sigma^2}\biggr)
$

これをグラフ化したいというのが今回の内容です。

統計分析をしていると、資料を書く時に必要となることも多いのですがPowerPointなどで作図すると正確性に欠けるし面倒です。できればきちんとしたベルカーブのグラフを使いたいと思い、Pythonで描画するプログラムを作成しました。

今回は、$1\sigma$, $2\sigma$に入る確率とかを説明する資料で欲しくなり作成に踏み切りました。自分で作れば、著作権とかを気にしなくてよくなるので。

グラフを書く

GitHubにGoogle Colabのコードを用意していますのでそちらも参考にしてください

なお、numpy, scipy, matplotlibは既にインストール済みという前提になります。インストールしていない場合は、以下のコードを実行してインストールしてください。

pip install numpy matplotlib scipy

必要なパッケージをインポート

まず、必要なパッケージをインポートします

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats

グラフデータの準備

正規分布のグラフデータを作成しています。具体的には、平均値mu、偏差sdのグラフを作成しています。$3\sigma$まで入れたいのでXの範囲は-4~4としています。scipy.stats.norm.pdfは確率密度関数を返してくれる関数です。

これで、X,Yが生成されます

mu = 0
sd  = 1

X = np.arange(-4,4,0.1)
Y = scipy.stats.norm.pdf(X, loc=mu, scale=sd)

グラフの描画

データが準備できたので、グラフ描画になります。サイズ等はfigsizeで調整しています。tickで横軸のメモリを調整して、あとはmatplotlibで描画です。

fig = plt.figure(figsize=(10, 4), facecolor="white")

tick = [i for i in range(-4, 4, 1)]

ax = plt.subplot()
ax.set_xticks(tick)

ax.plot(X, Y, c=colors)
ax.grid(axis='x', c='lightgray')
ax.grid(axis='y', c='lightgray')
[ax.spines[side].set_visible(False) for side in ['right','top']]

plt.show()

グラフは以下のようになります