相加相乗平均|相加平均と相乗平均のどちらが大きい？直感的に理解する方法

Aru

この記事では、「相加相乗平均はどのようなときに利用するのか？」「相加相乗平均の不等式の証明方法は？」「直感的に理解する方法は？」についてわかりやすく解説します。

まず、結論は以下のようになります。これは、相加相乗平均の不等式と言われます。

相加平均と相乗平均のどちらが大きい？

「相加平均 $ \geqq $ 相乗平均」

$$ \begin{eqnarray} \frac{a+b}{2} \geqq \sqrt{ab}\\
※a>0, b>0 \end{eqnarray}$$

Contents

相加相乗平均
- 相加平均、相乗平均とは？
- どんな時に使う？
証明
直感的なイメージ

相加相乗平均

相加平均、相乗平均とは？

相加相乗平均の不等式（Arithmetic Mean-Geometric Mean Inequality, AM-GM）は、高校生で習うやつです。

「相加平均」は足し算した時の平均で、「相乗平均」は互いに掛け算した時の平均です。どちらが大きかったか忘れがちです。

$$ \begin{eqnarray} \frac{a+b}{2} \geqq \sqrt{ab}\\
※a>0, b>0 \end{eqnarray}$$

「相加平均 $ \geqq $ 相乗平均」です

どんな時に使う？

次のような最小値を求める問題や、不等式の証明などに利用できます。

問題

$x>0$の時、$a = 2x, b = \frac{1}{x}$の場合のa+bの最小値を求めなさい。

$x > 0$であれば、$a > 0$, $b > 0$です。なので、相加相乗平均の式が使えて、以下のようになります。

$$ \begin{eqnarray}
\frac{a+b}{2} &\geqq & \sqrt{ab}\\
a+b &\geqq & 2 \sqrt{ab}\\
a+b &\geqq & 2\sqrt{2x \cdot \frac{1}{x}} \\
a+b &\geqq & 2\sqrt{2}
\end{eqnarray}$$

証明

これの証明は結構簡単です。以下、一気に書きます。

$$ \begin{eqnarray}
\frac{a+b}{2} &\geqq& \sqrt{ab}\\
(a+b) &\geqq & 2\sqrt{ab}\\
(a+b)^2 &\geqq & (2\sqrt{ab})^2\\
a^2 + 2ab + b^2 &\geqq & 4ab\\
a^2 – 2ab + b^2 &\geqq & 0\\
(a-b)^2 &\geqq & 0
\end{eqnarray} $$

$a \gt 0,b \gt 0$なので、$(a-b)^2$も当然０より大きくなります。以上、以下の式が成り立つことが証明できました。

$$\begin{eqnarray} \frac{a+b}{2} \geqq \sqrt{ab}\\
※a>0, b>0\end{eqnarray}$$

直感的なイメージ

これを図形的に解説しているページがあり、分かりやすかったので紹介しておきます。

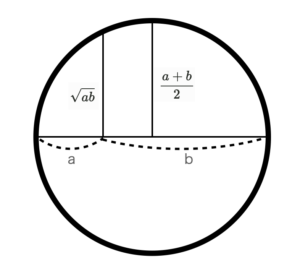
円の中心を通る水平線を適当にa,bで区切っています。円の中心を通る水平線なので、$a+b$は直系になります。

円の中心から円周にのばした線の長さは半径に一致するので、長さは直径の半分で$\frac{a+b}{2}$になります。

次に、aとbに区切った線から垂直に円周までのばした線の長さですが、これは$\sqrt{ab}$になります（頑張って証明してもよいですがここでは省略します。気になる方は参考にしたページを参照してください）。

これを見ると任意のa,bに区切った場合、必ず$\frac{a+b}{2}$より短くなることが直感的にわかるかと思います（最大で半径ですので）。

参考にしたページ：【図でわかる】相加相乗平均と円

図形（画像イメージ）として、感覚的に覚えておけば忘れにくいので、図形で覚えることをお勧めします。この場合、$\frac{a+b}{2}$が半径で、中心を通る直線から垂直に引いた線分から円の交点までの距離で、半径より大きいものはないことが直感的にわかるので、相加相乗平均のどちらが大きいかすぐに思い出せるようになります。

#相加相乗平均