パチンコのLTの出玉数をモンテカルロ法で計算してみた｜確率・統計を活用しよう
Aru
Aru's テクログ（Aruaru0）
重複組み合わせとは？計算方法を例で理解しよう
Aru
競技プログラミングでは「数え上げ問題」がよく出題され、その中でも「重複組み合わせ」は特に混乱しやすい問題の１つだと思います。初めて挑戦する人にとっては「どうやって解くの？」と悩んでしまうかもしれませんが、ポイントを押さえれば簡単です。この記事では、重複組み合わせの基本的な考え方をわかりやすい例とともに解説します。
重複組合せ問題にチャレンジ
出題内容
ここでは、数え上げ問題で出題される、重複組み合わせの問題を１つ紹介したいと思います。
ここで解く問題は以下になります
問題
この机では、Ｐ人の受験生が試験を受けることになっています。
机には横一列にＣ席が並んでいます。受験生の配置では、隣の人の答案が見えないように受験生間で席を１つ以上空けて座らせる必要があります。
受験生を座らせる席のパターンはいくつありますか。なお、受験生は個々に区別しないこととします。
１つ以上間隔を空けて受験生を座らせた場合の、組み合わせの数を数え上げる問題です。
整理できれば、簡単なのですが悩みました。
具体例で考える
理解するために、具体的に人数を当てはめて考えてみます。ここでは、受験生5人、席数１１席としました。
まず、受験生を座らせるには何席必要かを考えます。両端に受験生を配置するとすれば、空席と交互に配置した以下のパターン、つまり９席が最低必要な数になります。
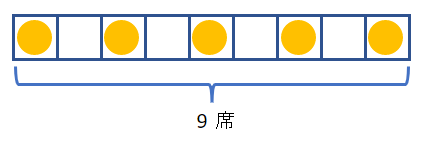
このパターンをベースに考えます。９席のパターンは決まっているので、１１席の場合、２席余分にあることになります。$P$と$C$の記号で考えると$C-(2P-1)$席です。
これは、空席の隣か、両端の好きな位置に挿入できます。空席の左右どちらに入れても（空席、空席）というパターンに変化はないので、どちらに入れる場合も区別しないで考えると、あまり２席を挿入できる場所は、下図の矢印部分の６箇所となります（$P+1$箇所）。
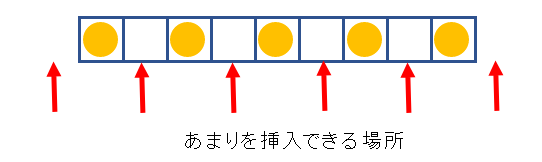
実は、空席の左右どちらに入れるかを区別しない、という部分で悩みました。受験者と空席の間の数＋両端の１０箇所じゃないかと最初思ってしまいました。
ただ、ちゃんと考えると、どちらに挿入しても、空席が２つになることは同じなので区別しません（下図）。なので、６箇所になります。
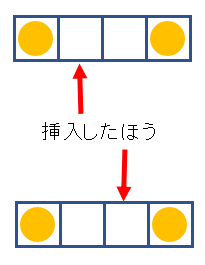
ここまで整理できればあとは簡単です。
$P+1$箇所の中に、$C-(2P-1)=C-2P+1$個を配置する組み合わせの数ですので重複組み合わせで以下のように表すことができます。
$$ _{P+1}H_{C-2P+1} $$
ちなみに、重複組み合わせ$H$は以下のように書くこともできます。
$$ _nH_r = _{n+r-1}C_r $$
ちょっと複雑になっただけで分からなくなってしまいます。
このあたりを簡単に解けるようになりたいね。
ABOUT ME
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
