「相関が高い」は相関係数がいくつから？答えは「場合による」が正解

よく、「あれとこれの相関は高い」などと言うことがあります。相関は相関係数で数値化することができますが、幾つなら高いのでしょうか？

答えは、「場合による」です。

ここでは、相関の高さと相関係数について話したいと思います。

そもそも相関係数って

相関係数は、２つの確率変数の間にある線形な関係の強弱を図る指標です。

相関係数は$-1 \sim 1$の間をとる実数で、相関係数が正のときに正の相関、負の時に負の相関があるといいます。で、０が無相関で、一番関係がない状態となります。

注意するポイントは、-1が一番相関がない状態ではないことです。-1は負の相関がある状態で、「Aが上がるとBが下がる」といった、逆の動きをすると言うことです。つまり、相関係数が-1と1の場合は、片方が上下すると反対側も同様に上下（または逆に上下）すると言うことで、両者の関係は非常に高いことになります。

相関係数の計算式は、共分散を$\sigma_{XY}$、標準偏差を$\sigma_X, \sigma_Y$とおくと、以下になります。

$$
\rho = \frac{\sigma_{XY}}{\sigma_X \sigma_Y}
$$

これについては２変数の確率分布にも書いていますのでそちらも参照してください。

あわせて読みたい

２変数の離散型確率の平均と分散、相関係数を求める演習

相関の尺度は？

「相関の強さはどれくらいか」ってよく聞かれますが、大体以下のように定義されています

注意するのは、「大体」と言うことです。この値の範囲であればこう言うと決まっているわけではありません。

相関はいくつあればいいの？

では、具体的に相関がいくつだったら相関ありと言っていいのでしょうか？また、いくつ以下だったら相関ありとは言えないのでしょうか？

結論から言えば、以下になります。

相関の高さの基準は明確ではありません。実は、これが相関係数の使いにくいところです。また、相関関係があるとは言えない場合でも、2つの変数には関連があり、非線形な関係が存在する場合もあります。

線形ではないけど関係がある場合、相関は低くなることがある

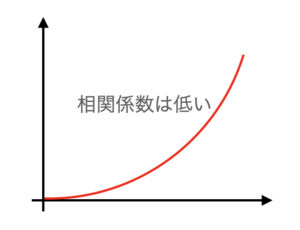
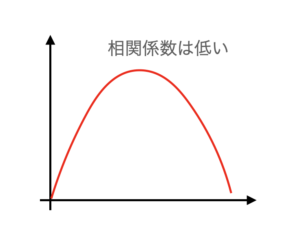
例えば、放物線上に乗るような形でXとYが関連している場合、線形（まっすぐな直線）を基準に判断する相関係数では、この曲線的な関係を捉えることができません（下図）。その結果、相関係数が小さい（関係が小さい）と判断されることになります。実際には2つの変数に関係があるにもかかわらず、相関係数ではそれが判断できないのです。

外れ値があると相関係数は低くなる

相関係数は外れ値に弱いという部分もあります。Aのグラフは、$y=x$となる10点のうち、１つだけずれているパターンです。Bのグラフは、$y = x + \epsilon$と、ノイズε加えたグラフです。

Aのグラフは、１つの点を除けば相関係数1.0になりますが、1つ外れ値のせいで0.71まで低下しています。一方、全体にノイズを加えた場合は、相関係数は0.85とそこまで落ちません。

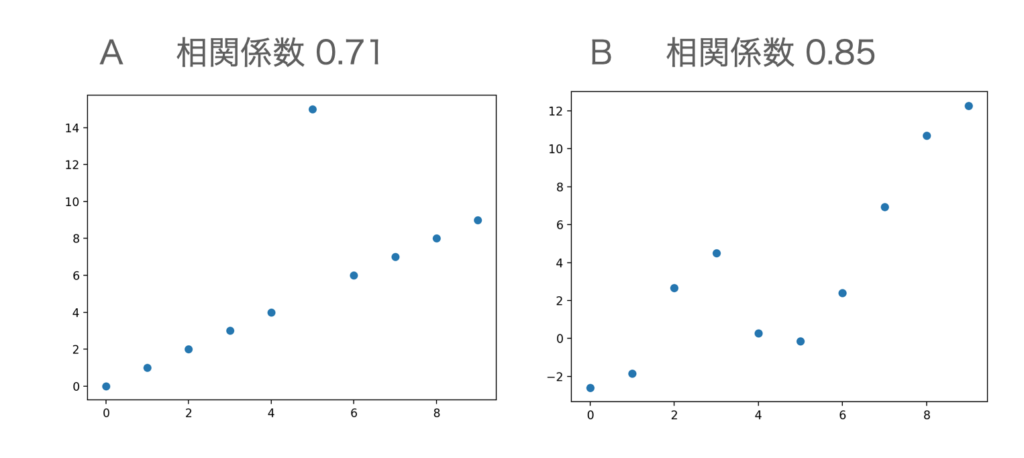
大きな外れ値があると、相関が低く見えてしまいます。かならずグラフで確認する習慣をつけておきましょう。

もともと相関が出にくいもの

2変数のうちどちらか、または、両方が人に対するアンケート結果などの場合、ばらつきが大きくなるため、相関は低くなる傾向があります。これは、アンケートが個々人の主観に基づいており、統一された基準で回答されていないためです。

例えば、「今眠いですか？」という質問に10段階評価を行うアンケートでは、同じ8を選んだ人々の眠さが必ずしも同じであるわけではありません。同じ状態でも回答は6や7、8とばらつくことになります。このような変数間の相関を計算すると、高い値（例: 0.8）となることはまれです。

経験的には、このような主観が関与する問題では、相関係数が0.4や0.5など低くなる傾向があると感じられます。

感覚的に、工学的な世界では相関は0.7とか0.8で相関ありと判断する傾向があり、人の主観などが介在する医療などの分野では0.3などでも相関ありと判断する傾向があると感じています。

対象によって、相関係数の値の見方も違うということですね。

P値について

上記のような場合に、どうするかというと、P値というのを参考にします。
P値というのは統計的仮設検定において、「帰無仮説のもとで統計量がその値となる確率のこと」です。簡単に言えば、偶然その値になる確率みたいな感じだと思ってもらえればよいです。普通はP値が0.05(5%)や、0.01(1%)以下であれば、検定を通過したと考えます。

相関係数とP値

例えば、相関係数が0.4であっても、P値が0.05の場合は、「相関がない」とは断定できず、「弱い相関がある」という表現ができます。このように、P値を考慮することで、相関の存在を示すことが可能です。

P値の罠

ただ、P値にも実は問題があります。P値はデータ数が多くなると小さな値になります。例えばデータサンプルが1000や10000もあれば、相関係数がどんなに低くても結構な確率でP値は0.05を下回ります。なので、P値が低いからといって、必ずOKではないということも注意が必要です。

その他

統計的仮設検定では、第２種の誤りというものもあります。こちらを使って検定結果を確認することも行われます。こちらについては、またどこかで説明したいと思いますが「検出力」というキーワードで覚えておきましょう。

まとめ

いかがでしたでしょうか。

相関係数が0.7を超えたから２つの関係性が高い、相関係数が0.2だから２つの関係性が低いと言うのは言えないことがあると言うことがわかりましたでしょうか。

実際に、仕事で相関係数を扱うことがある場合、このあたりが結構重要になります。特に、アンケートなど、主観の入ったデータを取り扱う場合は、相関係数が0.75を超えないからと言って相関がないわけではないことに注意が必要です。