2025.07.25

記事内に商品プロモーションを含む場合があります

LMStudioのjs-code-sandboxを試してわかった「利点と欠点」

Aru

LMStudioでMCP（Multi-Component Plugin）がサポートされましたが、インストール直後の状態で rag-v1 だけでなく js-code-sandbox も利用可能だったため、試してみました。この記事では、Gemma 3n-E4B と Qwen3-30B-A3B の2つのモデルを使って、その挙動を検証した結果をご紹介します。

Contents

LMStudioのMCP対応
- js-code-sandboxを有効にする手順
Qwen3-30B-A3B での検証
- 10!を計算させてみる
- 積み立て複利の計算
Gemma 3n E4Bの検証
- 10!を計算させてみる
- 積み立て複利の計算
まとめ

LMStudioのMCP対応

2025年6月、LMStudioにMCP機能が追加されました。MCPは、LMStudio内のLLMと外部ツールやプログラムを連携させるためのインターフェースです。

最初は rag-v1 のみが標準搭載されていましたが、バージョン 0.3.18 以降で js-code-sandbox が追加され、JavaScriptコードの実行が可能になりました。

今回は、この js-code-sandbox がどのようなタイミングで呼び出され、どの程度使えるのかを試しました。

js-code-sandboxを有効にする手順

左側のメニューから program を選び、js-code-sandbox のトグルをONにするだけで設定完了です。以降、必要に応じてJavaScriptが自動で実行されるようになります。

LLMが必要と判断して呼び出される仕組みなので、思ったように呼び出されないことも多いです。

Qwen3-30B-A3B での検証

どういう場合にJavaScriptを使うかといえば、おそらく計算が必要なときだろうということで、計算が必要となる問い合わせを行ってみました。

10!を計算させてみる

以下のプロンプトで10!を計算させてみます。

入力プロンプト

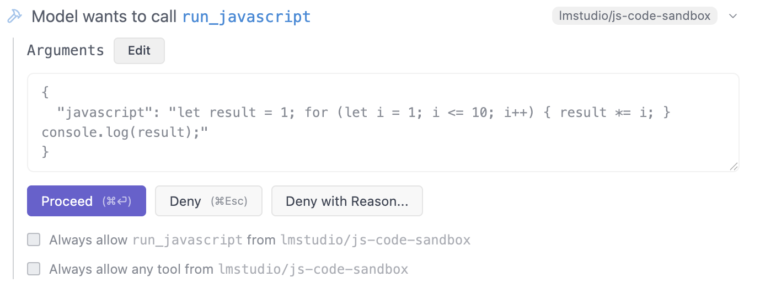
10!を求めて

実行時にJavaScriptの利用確認が表示されるので、ここでProceed をクリックします。

その後、回答が返ってきました。

回答結果

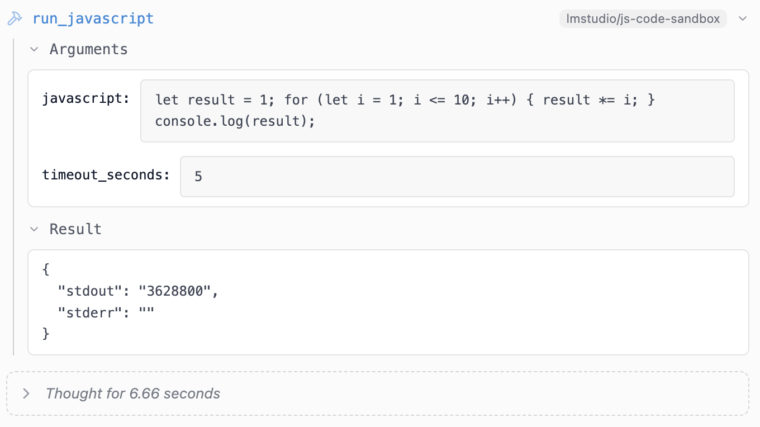
10!の値は3628800です。

10!=10×9×8×7×6×5×4×3×2×1=3628800

run_javascript の内容を見ると、JavaScriptで計算されていることが確認できます。

積み立て複利の計算

つぎは、少し難しめの質問をしてみます。

入力プロンプト

月々5万円を年金利5%で10年間積み立てたらいくらいになる？

問い合わせを行うとしばらく考えたのち、JavaScriptの実行許可を求めてきます。そして結果が表示されます。

回答結果

月々5万円を年利5%で10年間積み立てた場合、最終的な金額は7,764,113.97円となります。この計算では、毎月の積立金に複利がかけられ、合計120回の支払いを前提としています。ただし、金利の計算方法（月単位の複利）や支払いタイミング（期末または期初）によって結果が変わる可能性があるため、詳細な条件が必要な場合は別途確認してください。

この時、LLMが生成したプログラムは以下になります。

function calculateFutureValue() {
  const monthlyPayment = 50000;
  const annualRate = 0.05;
  const years = 10;
  
  const monthlyRate = annualRate / 12;
  const totalPayments = years * 12;

  // Future Value of an Ordinary Annuity formula
  const fv = monthlyPayment * ((Math.pow(1 + monthlyRate, totalPayments) - 1) / monthlyRate);
  
  return fv.toFixed(2);
}

console.log(calculateFutureValue());

計算式を見ると年利を12で割って、月単位の利率に変換し、10年に12ヶ月をかけて期間を120ヶ月にしています。また、以下の式は、年金終価係数を使っており適切な計算ができていることがわかります。

const fv = monthlyPayment * ((Math.pow(1 + monthlyRate, totalPayments) - 1) / monthlyRate);

年金終価係数の計算についてはこちら

ファイナンシャル・プランニングの「６つの係数」｜数式を理解して知識に差をつけよう

このように、計算が必要な問い合わせについて適切にJavaScriptを作成し、呼び出してくれました。

続けて、もう少し複雑な問い合わせをしてみます。

入力プロンプト

では、平均年金利5%、リスク10%で運用した場合は？　1σの範囲を計算して教えて。

今回はJavaScriptで計算せずに回答してきました。こちらが狙った通りにならないというのがMCPによる呼び出しあるあるです。

回答結果

計算式：

1σ範囲 = 平均収益率 ± 標準偏差
= 5% ± 10%
= -5% 〜 +15%

解釈：

この範囲内に約68%の確率で収益が含まれます（正規分布の性質）。
例：1年後の運用結果が-5%から+15%の間に入る確率は約68%です。
リスクが10%とは、収益の変動幅が大きいことを示し、市場のボラティリティを反映しています。

注意点：

実際の市場では正規分布に従わない場合もあり、極端な損失（ブラック・スワン現象）の可能性も考慮する必要があります。

これは単年度の収益率の範囲です。10年間の複利運用におけるリスク範囲は、より複雑な計算（例えば、年間の変動率を考慮したシミュレーション）が必要です。

づつけて、以下のように問い合わせてみました。

入力プロンプト

シミュレーションにより10年後の金額を求めて

今回は JavaScript を使いましたが、結果が異常 でした。平均：178億円、標準偏差：664億円など、明らかに誤った計算。流石に月5万円づつ投資しても10年で178億円にならないのは直感的にわかりますので検算する必要もありませんでした。

回答結果

シミュレーションにより、平均年利5%（リスク10%）で運用した場合の10年後の金額分布を算出しました。ただし、シミュレーションでは以下の点に注意が必要です：

結果概要

平均値：約178億円
標準偏差：約664億円

この結果は、年利5%の平均収益率と10%のリスク（標準偏差）を前提としたモンテカルロシミュレーションによるものです。ただし、以下のような仮定と制限があります：

シミュレーションの前提

月次積立：毎月5万円を積み立て（年利5%の固定金利時と同じ条件）。
変動収益率：毎年、平均5%・標準偏差10%の正規分布に従う収益率を仮定。
複利計算：各年の収益率を月次で複利計算（※実際の運用ではリスク管理や市場変動により異なる）。

結果の解釈

1σ範囲（約68%確率）：
平均値 ± 標準偏差 = -486億円〜842億円
（※負の値は市場崩壊などの極端なリスクを反映）
2σ範囲（約95%確率）：
平均値 ± 2×標準偏差 = -1,150億円〜1,506億円

注意点

収益率のモデリング：シミュレーションでは毎年の収益率を正規分布で生成しましたが、実際の市場は**裾野リスク（ブラックスワン現象）**や非対称性を持つため、極端な損失の可能性が考慮されていません。
複利計算の簡易化：月次積立と年間収益率の複利計算を単純化して処理しましたが、より詳細なシミュレーションには日次・時間単位の収益率モデルが必要です。
結果の信頼性：10,000回のシミュレーションで算出された平均値は、リスク許容度に応じた投資戦略の参考として利用してください。

追加のシミュレーションが必要な場合

シーンに応じたリスク管理指標（例：VaR、シナリオ分析）の算出。
複数年の収益率連動やボラティリティの変化を考慮したモデル。

必要に応じて、より詳細なシミュレーションをご提案します。

プログラムを確認すると以下のようになっていました。

プログラムを斜め読みするとモンテカルロシミュレーションを正しく実装しているように見えます。

モンテカルロ法についてはこちら

3000万円で何年暮らせる？モンテカルロ法による資産シミュレーション【Python】

ただ、よく見ると、年利の計算がおかしいです。以下、気づいた誤りです。

正規分布の代わりに一様分布を使用
年利を「月単位で」掛けている（月5±10%の金利になっている）

なお、結果が億円と極端に大きくなったのは２つ目の影響が大きそうです。

function simulateFutureValue() {
const monthlyContribution = 50000;
const annualReturnMean = 0.05;
const annualReturnStdDev = 0.10;
const years = 10;
const simulations = 10000;


let results = [];


for (let i = 0; i < simulations; i++) {
let total = 0;
let returns = [];


// Generate annual returns for 10 years
for (let y = 0; y < years; y++) {
  // Normal distribution with mean 5% and std 10%
  let annualReturn = (Math.random() * 2 - 1) * annualReturnStdDev + annualReturnMean;
  returns.push(annualReturn);
}

// Calculate future value of monthly contributions with these returns
for (let month = 0; month < years * 12; month++) {
  let year = Math.floor(month / 12);
  let monthlyReturn = returns[year];
  total += monthlyContribution;
  total *= (1 + monthlyReturn);
}

results.push(total);

}


// Calculate mean and standard deviation of results
let sum = results.reduce((a, b) => a + b, 0);
let mean = sum / simulations;


let variance = results.reduce((a, b) => a + Math.pow(b - mean, 2), 0) / simulations;
let stdDev = Math.sqrt(variance);


return { mean: mean.toFixed(2), stdDev: stdDev.toFixed(2) };
}


console.log(JSON.stringify(simulateFutureValue()));

Qwen3 30B-A3Bではうまくコード生成ができなかったみたいです。LLMは計算が不得意なので、JavaScriptでプログラムを作成・実行してミスを減らせるかと思いましたが、コード自体に誤りがあるとツールの有無に関わらず結果が破綻することが確認できました。

Gemma 3n E4Bの検証

軽量モデルとして注目されているGemma 3nでも試してみました。このモデルはサイズの割には賢いと評判です。こちらはツールサポートのアイコンはついていませんが、呼び出せるかチェックしてみました。

10!を計算させてみる

まずは簡単なパターンから実行です

入力プロンプト

10!を求めて

js-code-sandboxを呼び出して計算させ回答することができました。

回答結果

10! は 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 です。

10! は 3628800 です。

呼び出しはできるようです。

積み立て複利の計算

先ほどと同じプロンプトで質問してみました。

入力プロンプト

月々5万円を年金利5%で10年間積み立てたらいくらいになる？

結果は、JavaScriptの実行に失敗しました。コード出力にミスがあったようです。

やはり、小さいモデルには限界がありそうです。

まとめ

Qwen3 30B-A3B
　JavaScriptの呼び出しは可能だが、少し複雑なコードは正しく生成されず結果を誤ってしまった。

Gemma 3n-E4B
　MCPの恩恵をより受けることができると期待したが、コード出力ミスが発生

個人的には小さなモデルほどMCPの恩恵がある気がするのですが、逆にうまく呼び出せずに失敗してしまうなどの問題がありました。Qwen3 30B-A3Bは、一応呼び出せましたが少し複雑になるとプログラムコードミスで変な結果になってしましました。「計算ミスをサポートするために、js-code-sandboxは便利かな？」と思っていましたが、結果を見ると一長一短な感じでした。

#LLM #MCP