2024.04.07 2024.09.01

記事内に商品プロモーションを含む場合があります

PyMC（ベイズ統計モデリング）で回帰問題を解く｜Python

Aru

PyMCは、Pythonでベイズ統計モデリングを行うためのライブラリです。本記事では、PyMCを使って線形回帰問題を解いてみます。通常の線形回帰ではベイズ推定を行う必要はありませんが、あえてPyMCを使用することで、ベイズモデリングの基本とPyMCのコードの書き方を実践的に学べるようしました。なお、本記事では、Scikit-learnによる線形回帰と、PyMCで比較も行なっています。

Contents

PyMCとは
scikit-learnを使った線形回帰
- データの作成
- 線形回帰をやってみる
PyMCによる線形回帰（ベイズ統計モデリング）
まとめ

PyMCとは

PyMCは、Pythonでベイズ統計モデリングを行うためのライブラリです。PyMCは、マルコフ連鎖モンテカルロ（MCMC）サンプリングや変分推論などのアルゴリズムを使用して、ベイズ統計モデリングのための様々な手法を提供しています。

ベイズ統計では、未知のパラメータの確率分布を表すために確率モデルを使用します。データを観測すると、この確率モデルを通じて未知のパラメータの事後分布を推定することができます。PyMCを使用すると、このようなベイズ統計モデルを柔軟かつ効率的に記述し、推論を行うことができます。

これまでRStanを使ってベイズ統計モデリングをやっていましたが、最近はPythonを使うことが増えているので、PyMCも使ってみようと思い、とりあえず書き方と動作を確認するために回帰問題にトライしてみました。

RStanを学習した時も、線形回帰を最初にプログラミングしました。確認にはちょうど良いと思います。

scikit-learnを使った線形回帰

データの作成

以下の一時関数のデータを作成し、これを回帰予測するためのデータとして利用します。

$$
y = a x + b + N(\mu = 0, \sigma=1)
$$

式において、傾き$a=0.5$、切片$b = 2$とします。

$N(\mu=0, \sigma=1)$は、平均0、分散1の正規分布に基づく乱数になります。

この分布に基づくxとyを作成するコードは以下のようになります。コードでは、1,000サンプルを作成しています。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

np.random.seed(42)

x = np.random.randint(0, 100, 1000)/10
a,b = 0.5, 2
y = a*x + b + np.random.randn(1000)

作成したデータは$y = 0.5x + 2$に正規分布のノイズが加えられたものになります。

これで、データが準備できました。

線形回帰をやってみる

scikit-learnを使って、線形回帰予測を行ってみます

以下、コードです。

X = x.reshape(-1, 1)
reg = LinearRegression()
reg.fit(X, y)

y_pred = reg.predict(X)

print(f"a = {reg.coef_[0]}, b = {reg.intercept_}")

plt.scatter(x, y)
plt.plot(X, y_pred, color="red")
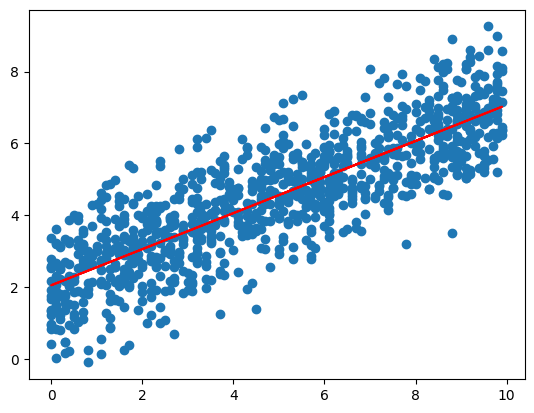
plt.show()

予測結果は、傾きが0.502…, 切片が2.049…と、ほぼ設定した値になりました。

a = 0.5021551846596773, b = 2.049708701433307

作成したサンプルと、回帰直線をグラフにプロットしたものが以下になります。

これを、pymcを使ってやってみます。

PyMCによる線形回帰（ベイズ統計モデリング）

全体コード

以下、PyMCを使った線形回帰のコードです。

import pymc as pm
import numpy as np

np.random.seed(42)

x = np.random.randint(0, 100, 1000)/10
a,b = 0.5, 2
y = a*x + b + np.random.randn(1000)

# X = x.reshape(-1, 1)

with pm.Model() as model:
    pred_a = pm.Normal("a", mu = 0, sigma = 10)
    pred_b = pm.Normal("b", mu = 0, sigma = 10)
    sigma = pm.HalfNormal("sigma", sigma=1)

    mu = pred_a * x + pred_b

    Y = pm.Normal("Y", mu=mu, sigma=sigma, observed=y)

with model:
    trace = pm.sample()

vars = ['a', 'b', 'sigma']

pm.plot_trace(trace, var_names=vars, backend_kwargs={"constrained_layout":True})
pm.summary(trace, var_names=vars)
pm.plot_posterior(trace, point_estimate='mode')

a = float(trace.posterior.a.mean())
b = float(trace.posterior.b.mean())
sigma = float(trace.posterior.sigma.mean())
print(f"a = {a}, b = {b}, sigma={sigma}")

動作確認は、Google Colabで行いました。Macbookで動作させようとしたのですが、インストールしてもエラーがでて動かなかったので諦めました。

データ作成

データの作成は、scikit-learnと同様ですのでここでは省略します。

モデルの定義

$y=ax+b$の$a$と$b$を予測するために、モデル化します。

モデル化の部分は、コード中の以下の部分です。

with pm.Model() as model:
    pred_a = pm.Normal("a", mu = 0, sigma = 10)
    pred_b = pm.Normal("b", mu = 0, sigma = 10)
    sigma = pm.HalfNormal("sigma", sigma=1)

    mu = pred_a * x + pred_b

    Y = pm.Normal("Y", mu=mu, sigma=sigma, observed=y)

ここでは、$a, b$は、平均(mu)0、偏差(sigma)10の正規分布に基づくと仮定しています（2,3行目）。

また、sigmaは0以上の偏差1の片側の正規分布に基づくと仮定します（4行目）。

偏差は0以上なので、負にならないようにしています。

最後に$y=ax + b + sigma$で、平均$ax+b$で偏差sigmaに従うと仮定します（6~8行目）。

以上で、モデル定義は終了です。

このようにモデル定義では、各変数がどのような分布に基づくかを記述していきます。

モデルのサンプル

モデルが定義できたので、サンプリングを行います。この処理は少し時間がかかります。

具体的には、pm.sample()を実行して、サンプリングにより事後分布を推定します。

結果はtraceに格納されます。

結果のプロット

プログラムでは、plot_trace, summary, plot_posteriorを使ってサンプリング結果、サマリー、事後確率を表示しています。

また、print（）で、a, b, sigmaをそれぞれ出力しています。

ベイズ統計モデリングを行う場合には、traceを見てサンプリングの結果を確認します。２チェイン動作さひているので、グラフは2つになっています。右側のグラフは推定値を中心に、偏りなくばらついている（表現が悪くてすみません）方が良いです。グラフを見る限り、うまく収束していそうです。

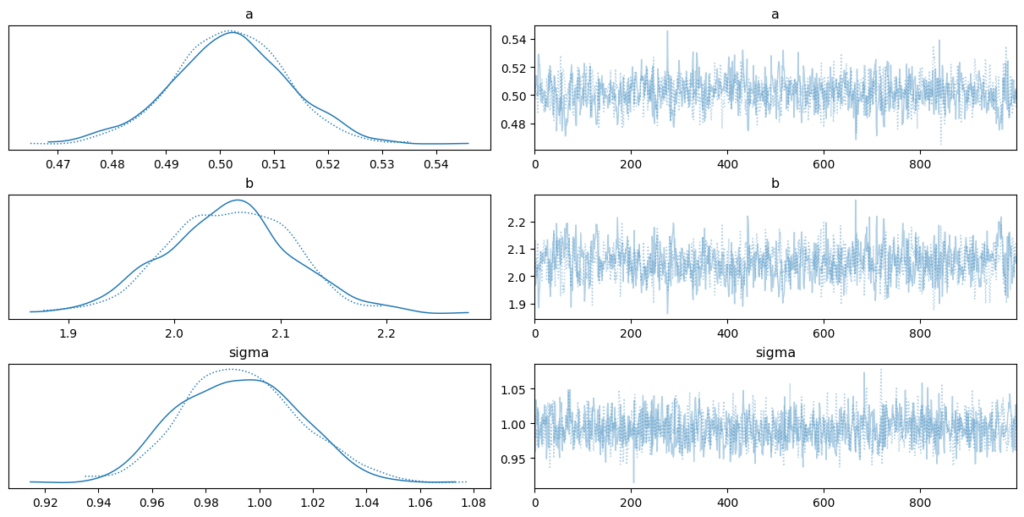
収束しているかどうかはsummaryでも確認することが可能です。

以下は、summaryの結果になります。

a, b, sigmaの平均、偏差、3~97%の値の範囲などが確認できます。r_hatは、結果の確認のための指標で1.0に近いほどよく、1.1未満であれば良好でこれより大きいと収束していない可能性があるというものです。今回は、全て1.0ですので、ここからも収束していることがわかります。

plot_posteriorの結果が以下です。これをみると予測したa, b, sigmaをグラフで確認できます。

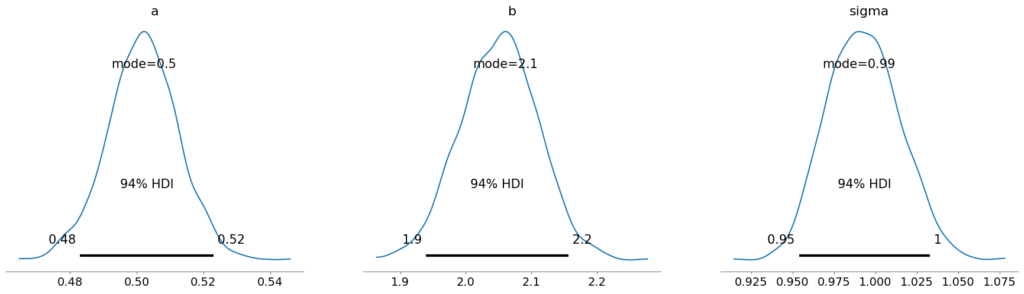
予測したa, b, sigmaの値は以下になります。

$a=0.5, b = 2.0, sigma = 1.0$でデータを作成したので、おおよそ正確な値が予測できていることがわかります。

a = 0.5018975956556755, b = 2.0510944334308197, sigma=0.9929723347372681

モデルを図示したい場合

モデルを図示したい場合は、以下のコードを実行します

pm.model_to_graphviz(model)

実行すると以下のようにモデルをグラフィカルに出力することが可能です。

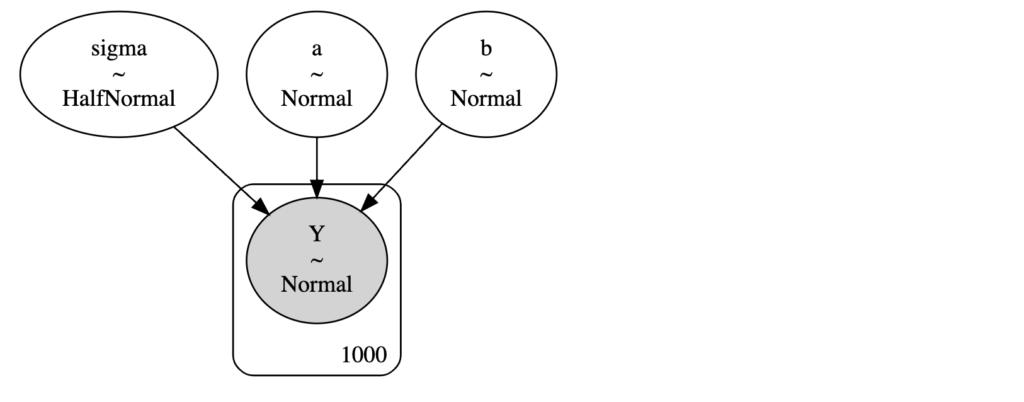
traceの中身

sampleの実行後の変数traceの中身は、Google Colabであれば、以下のようなコードで確認することも可能です。

trace

実行すると以下のような出力が得られます。マウス操作で、項目を開いたり閉じたりでき、中身を確認できます。

PyMCを使う例

PyMCで学ぶベイズ統計モデリング｜イカサマコインの判別にチャレンジ

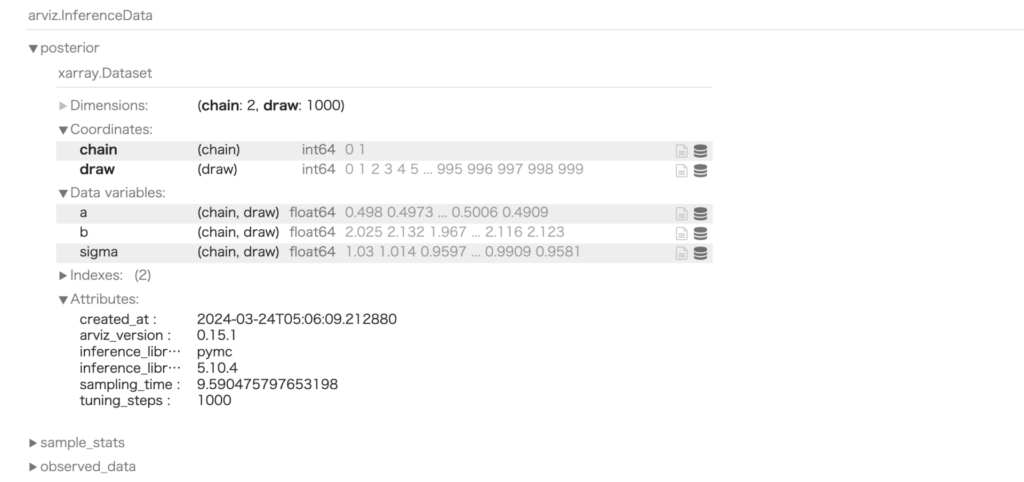
まとめ

線形回帰にベイズ統計モデリングを使ってみることで、モデルの書き方、コードの記述の仕方の確認をしてみました。

これまで使っていたRStanとは、書き方は違いますが、書く内容はほぼ同じです。モデルを記述す部分はRStanよりは、普通のプログラムっぽい記述なので、どちらかというととっつきやすいと思います。

変数が確率分布に従うという部分に慣れないとわかりにくいかもしれませんが、慣れるとかなり強力なツールです。

とりあえず、RStanからこちらに移行しようと思います。

#PyMC #python #ベイズモデリング #機械学習 #確率