MENU
プログラミング
記事内に商品プロモーションを含む場合があります

パチンコのLTの出玉数をモンテカルロ法で計算してみた｜確率・統計を活用しよう

確率・統計関連記事
Aru

YouTubeなどでパチンコの実践動画を観察すると、最近のパチンコ台の大当たりは非常に複雑な状態遷移をすることを知りました。複雑な条件の分析は、数式で解くよりもシミュレーション手法が楽です。この記事では、モンテカルロ法を用いて、ラッキートリガー（LT）機能を搭載したパチンコ台の平均出球数を計算してみます。結果だけをみたい方は、目次で「シミュレーション結果」にジャンプしてくさだい。

Contents
  1. はじめに
  2. 「この素晴らしい世界に祝福を」のスペック
  3. プログラムを作成（Python）
  4. シミュレーション結果
  5. まとめ

はじめに

確率・統計の題材として、「パチンコ」は非常に面白いテーマです。

特に最近のパチンコ台は、「通常or確変」などの単純なモデルにとどまらず、「確変の一定量が上位確変に突入」「上位確変から一定割合で転落」など、複雑なゲーム性を持っています。こうした複雑な状態遷移を計算するのは非常に興味深いですが、数式で表現するのは難しくなります。

このような場合に便利なのが、モンテカルロ法です。

モンテカルロ法では、多数のシミュレーションを繰り返すことで、近似的な結果を得ることができます。

詳しくは以下の記事を参考にしてください。

あわせて読みたい
3000万円で何年暮らせる？モンテカルロ法による資産シミュレーション【Python】
3000万円で何年暮らせる？モンテカルロ法による資産シミュレーション【Python】

この記事では、モンテカルロ法を使ってパチンコの期待値を求める方法について解説します。

今回、対象とするのは、Pこの素晴らしい世界に祝福を!199LT「このラッキートリガーに祝福を!」という台です。

今回の記事のためにネットで台のスペックを調べてみました。いろいろなパターンがあったのですが、状態遷移が結構複雑で、題材としてちょうどよいかなと思って、この台を選びました。

パチンコの当たる確率を数学的に求める記事

パチンコのST中に当たる確率の計算方法（N回転以内に当たる確率は？）
パチンコのST中に当たる確率の計算方法（N回転以内に当たる確率は？）
確率統計から見た、パチンコの継続回数の罠
確率統計から見た、パチンコの継続回数の罠

「この素晴らしい世界に祝福を」のスペック

調べてみましたが、かなり複雑です。

基本スペックは以下の通りです。

大当り通常時1/199.8
RUSH時1/67.3
このすば
RUSH		突入率100%
継続率約70%
祝福RUSH
(ﾗｯｷｰﾄﾘｶﾞｰ)		発動確率約8.1%
継続率約88.6%
電サポ77 or 1万回
賞球数1＆6＆2＆15/10C
基本スペック表

以下、「このすばRUSH」と「祝福RUSH」の確率表です。

このすばRUSHの確率表
ラウンド数電サポ払出割合
10R祝福RUSH
(1万＋4)回転		1500個0.5%
10RこのすばRUSH
(77＋4)回転		1500個49.5%
4R240or
330個		50.0%
4祝福RUSHの確率表
ラウンド数電サポ払出割合
10R祝福RUSH
(1万＋4)回転		1500個50.0%
4R祝福RUSH
(1万＋4)回転		240or
330個		38.6%
4RこのすばRUSH
(77＋4)回転		240or
330個		11.4%

大当たり、「このすばRUSH」、「祝福RUSH」という３つの状態があり、大当たりで100%このすばRUSHに突入し、「このすばRUSH」の一部が「祝福RUSH」に突入、「祝福RUSH」の一部がこのすばRUSHに転落するという仕様のようです。

出球数に関連するラウンド数も、4R（240個or330個）or10Rで、RUSHのモードとラウンド数の組み合わせがかなり複雑です。

さらに、「このすばRUSH」の77回転目と保留４回転で当たると、「祝福RUSH」のふりわけになるという、さらに複雑な仕様です。

最近パチンコを打つ人は、こういうのを理解して遊んでいるんですよね。結構すごいです。

題材としての複雑さは十分です。今回は、この台の平均出玉、平均継続数などをモンテカルロ法で求めてみたいと思います。

シミュレーションは、初当たりを引いたところから行うので、初当たりの確率は利用しません。

また、シミュレーションするプログラムでは、以下のような変更を行っています。

  • 1万＋４回転の場合は、ほぼ当たるので100%当選として計算
  • 払い出しは1発玉を消費するのでその分を差し引いて計算
  • パチンコ出玉規制（1日95,000発で強制終了）を考慮　※詳細不明だが一応実装

プログラムを作成（Python）

全ソースコード

プログラムはPythonで作成します。

以下が作成したプログラムの全ソースコードです。

import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn.objects as so
import japanize_matplotlib 

prob = 1.0/67.3

def rushA() :
    mode = -1
    output = 0
    for i in range(76) :
        if random.random() <= prob :
            p = random.random()
            if p <= 0.005 :
                mode = 2
                output = (15-1)*10*10 # (15-1)発x10カウントx10R
            elif p <= 0.5 :
                mode = 1
                output = (15-1)*10*10 # (15-1)発x10カウントx10R
            elif p <= 0.75 :
                mode = 1
                output = (6-1)*10*4
            else:
                mode = 1
                output = (6-1)*10*3 + (15-1)*10*1
    for i in range(5) :
        if random.random() <= prob :
            mode, output = rushB()

    return mode, output

def rushB() :
    mode = -1
    p = random.random() 
    if p <= 0.5 :
        mode = 2
        output =  (15-1)*10*10 # (15-1)発x10カウントx10R
    elif p <= 0.693 :
        mode = 2
        output = (6-1)*10*3 + (15-1)*10*1
    elif p <= 0.886:
        mode = 2
        output = (6-1)*10*4
    elif p <= 0.943:
        mode = 1
        output = (6-1)*10*3 + (15-1)*10*1
    else:
        mode = 1
        output = (6-1)*10*4
    return mode, output



def simulate() :
    sum, n, n2 = 0,0,0
    mode = -1
    while True :
        if mode != 2 :
            mode, output = rushA()
        else:
            mode, output = rushB()
        if mode == -1 : break
        if mode == 2 : n2 += 1
        sum += output
        n += 1
        # print(mode, output)
        if sum > 95000 : break # 規制？

    return sum, n, n2

if __name__ == '__main__' :
    tot = []
    count1 = []
    count2 = []
    count2d = []
    N = 1_000_000
    for i in range(N):
        sum, n, n2 = simulate()
        sum += 7*10*5
        tot.append(sum)
        count1.append(n)
        if n2 != 0:
            count2.append(1)
        else:
            count2.append(0)
        if n2 != 0 :
            count2d.append(n2)
        # print("-"*80)
        # print(f"sum = {sum}, n = {n}, n2 = {n2}")
        
    df = pd.DataFrame({"出玉数": tot, "継続回数": count1, "ラッキトリガー突入回数": count2})
    print(df.describe())

    df2 = pd.DataFrame({"ラッキトリガー継続回数": count2d})
    print(df2.describe())
    print("ラッキートリガー突入率", len(count2d)/N)
    
    
    so.Plot(df, x="出玉数").add(so.Bars(), so.Hist(stat="percent", binwidth=2000)).theme({'font.family': 'IPAexGothic'}).show()
    so.Plot(df2, x="ラッキトリガー継続回数").add(so.Bars(), so.Hist(stat="percent", binwidth=5)).theme({'font.family': 'IPAexGothic'}).show()

以下、このプログラムについて解説します。

このすばRUSHの大当たりを計算（rushA）

一番面倒な、このすばRUSHの計算です。スペックを確認すると、「77回転目＋保留４つについては、祝福RUSHの確率表を使う」とのこと

プログラムでは、76回転までは確率（1/67.3）を引いたら当たり判定し、さらに乱数を引いて振り分けをチェックしています。

77回転以降は、当たりを引いたら祝福RUSHの確率表を引いています。

この関数の戻り値は、次のモード（mode）と、出玉（output）です。

modeは-1が外れ、1が次回もこのすばRUSH、2が次回は祝福RUSHです。

なお、出玉計算は(１５−１発）×１０カウント×ラウンド数で計算しています（消費する１発を引いています）。

なお、4R（240個と330個の振り分けとラウンド内訳）が書かれていなかったので、とりあえず50%:50%で計算し、出玉が240, 330個になるように調整しました。

def rushA() :
    mode = -1
    output = 0
    for i in range(76) :
        if random.random() <= prob :
            p = random.random()
            if p <= 0.005 :
                mode = 2
                output = (15-1)*10*10 # (15-1)発x10カウントx10R
            elif p <= 0.5 :
                mode = 1
                output = (15-1)*10*10 # (15-1)発x10カウントx10R
            elif p <= 0.75 :
                mode = 1
                output = (6-1)*10*4
            else:
                mode = 1
                output = (6-1)*10*3 + (15-1)*10*1
    for i in range(5) :
        if random.random() <= prob :
            mode, output = rushB()

    return mode, output

祝福RUSHの大当たりを計算（rushB）

本来は１万回＋４回回転ですが、100％当選として見積もるので当たり判定はありません。

確率表に従って、次回のモードと出玉を返します。

def rushB() :
    mode = -1
    p = random.random() 
    if p <= 0.5 :
        mode = 2
        output =  (15-1)*10*10 # (15-1)発x10カウントx10R
    elif p <= 0.693 :
        mode = 2
        output = (6-1)*10*3 + (15-1)*10*1
    elif p <= 0.886:
        mode = 2
        output = (6-1)*10*4
    elif p <= 0.943:
        mode = 1
        output = (6-1)*10*3 + (15-1)*10*1
    else:
        mode = 1
        output = (6-1)*10*4
    return mode, output

以上で、２つのラッシュについて実装完了です。

初当たり１回のシミュレーション（simulate）

初当たり１回の、出玉と継続数（このすばRUSH, 祝福RUSH）をシミュレーションする関数です。modeが-1になったら抜けます。

mode=1の場合はこのすばRUSHを、mode=2の場合は祝福RUSHの当たりをシミュレーションします。

def simulate() :
    sum, n, n2 = 0,0,0
    mode = -1
    while True :
        if mode != 2 :
            mode, output = rushA()
        else:
            mode, output = rushB()
        if mode == -1 : break
        if mode == 2 : n2 += 1
        sum += output
        n += 1
        # print(mode, output)
        if sum > 95000 : break # 規制？

    return sum, n, n2

以上の関数で初当たり１回のシミュレーションができます。

100万回シミュレーションして結果を出力

メイン関数です、100万回の初当たりをシミュレーションして、シミュレーション結果から統計データを計算します。

モンテカルロ法では、シミュレーションした結果を集計することで、近似値を求めることが可能です。

if __name__ == '__main__' :
    tot = []
    count1 = []
    count2 = []
    count2d = []
    N = 1_000_000
    for i in range(N):
        sum, n, n2 = simulate()
        sum += (6-5)*10*7
        tot.append(sum)
        count1.append(n)
        if n2 != 0:
            count2.append(1)
        else:
            count2.append(0)
        if n2 != 0 :
            count2d.append(n2)
        # print("-"*80)
        # print(f"sum = {sum}, n = {n}, n2 = {n2}")
        
    df = pd.DataFrame({"出玉数": tot, "継続回数": count1, "ラッキトリガー突入回数": count2})
    print(df.describe())

    df2 = pd.DataFrame({"ラッキトリガー継続回数": count2d})
    print(df2.describe())
    print("ラッキートリガー突入率", len(count2d)/N)
    
    
    so.Plot(df, x="出玉数").add(so.Bars(), so.Hist(stat="percent", binwidth=2000)).theme({'font.family': 'IPAexGothic'}).show()
    so.Plot(df2, x="ラッキトリガー継続回数").add(so.Bars(), so.Hist(stat="percent", binwidth=5)).theme({'font.family': 'IPAexGothic'}).show()

シミュレーション結果

100万回のシミュレーション結果は以下になります。

ネットを調べると、平均獲得玉数2859、平均継続回数4.02となっていました。また、祝福RUSHの平均継続回数は12.83回となっています。

シミュレーションの結果を見ると、継続回数についてはネット情報と同じくらいです。

ただ、平均出玉数については、シミュレーションした結果では4154個、ネット情報は2869個と差があります。もしかしてと思い、祝福RUSH抜きでシミュレーションしてみると平均出玉が2416個となりネット情報と近くなりました。

よくわかりませんが、上位ラッシュ抜きでの平均出玉数になっているのかもしれません。まぁ、複雑なのでその可能性もあるかもしれません。その点、モンテカルロ法は、複雑になっても対応できるのがメリットです。

あるいは、作成したプログラムにミスがあるかです。もし、ミスを見つけた場合はコメント欄で知らせてください。

2024/10/28：コメント通り240発、330発のラウンド数にミスがあったようなので修正しました。

出玉数継続回数ラッキートリガー突入ラッキートリガー継続回数
試行回数1,000,0001,000,0001,000,000183923
平均3,9204.30.18310.8
偏差6,5307.60.38710.2
最小350001
25%350003
50%1,750208
75%4,0405015
最大96,7001221108
モンテカルロシミュレーションの結果のまとめ
  • 平均出球は4,154発
  • 大当たりの50％は1,750発以下
  • 大当たりの75%は4,040発以下
  • 平均継続回数 4.3回

結果の見方は、各列が出玉数、継続回数、突入率、継続回数に対応していて、各行がそれぞれの平均・偏差、最小、25%、50%(中央値）、75%, 最大となります。例えば、出玉数の50%は1,750個で、半分は1,750発以下の出球で終わることを意味します。

結果をもう少し詳し見てみます。このすばRUSHの継続率は約70%なので、30%は当たらずに終わります。出玉数をみると25%の確率で350発以下ということなので、連チャンせずに終了していることが分かります（意外とシビアなゲームです）

また、平均は4,040発ですが、50%は1,750発以下の出玉です。平均と中央値がずれているというのは、最大96,700のような例外値によって平均が引き上げられるためです。この手のものは中央値で考えた方がよいです。

平均4,154なのに2000発しか出ないといったことが頻繁に起こる理由は、50%は1,750発以下だからです。

100万回試行したモンテカルロ法で、そこまで大きくずれるとは考えずらいですよね。前提などで、どこか違う部分があると考えた方がよいですね。

出玉だけでみても350発〜4,410発が75%で、4,411〜96,670発が25%と非常にムラの大きな分布になっていることも分かります。

下のグラフは、出玉数のヒストグラムと、ラッキートリガーの継続回数のヒストグラムです。出玉数は2000発単位、ラッキートリガーは5回単位でグラフ化しています。

出玉数のヒストグラム
ラッキートリガーの継続回数のヒストグラム

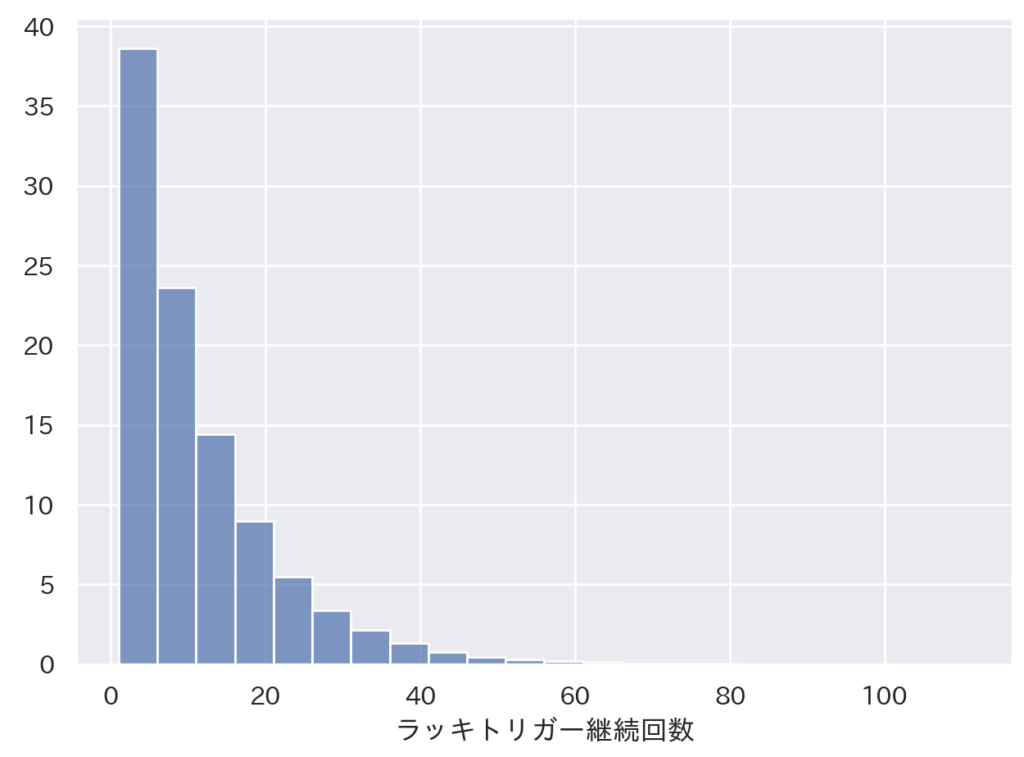
これをみると60%は出玉2,000発以下であることが分かります。また、ラッキトリガーにせっかく入っても約37%は継続五回以下で終了していることが分かります。

このスペック、実際の体感だと、全然出る感じがしない気がしますが、どうでしょうか？

まとめ

モンテカルロ法をつかって、複雑な確率を持つパチンコ台をシミュレーションし、平均出玉や継続回数を計算してみました。

金融とギャンブルは確率・統計が非常に役にたつ分野だと思います。この手の話題を通じて確率・統計に興味を持ってもらえたら嬉しいです。

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

  1. nkmr 2か月前

    https://www.p-world.co.jp/machine/database/9974
    この機種とは違いますか？
    そもそものラウンド数が違うように見えるのですが。

    返信する
    • Aru 2か月前

      この台です。ご指摘ありがとうございます。確かにスペックが若干違いますね（出玉は同じですが、ラウンド数が違う）。ラウンド数修正し、プログラムを変更、シミュレーションをやり直しました。ちなみに、出球数が変わらないので、修正しても結果は誤差範囲の違いでした。

      返信する
ABOUT ME
ある/Aru
ある/Aru
IT＆機械学習エンジニア/ファイナンシャルプランナー（CFP®)
Contact
専門分野は並列処理・画像処理・機械学習・ディープラーニング。プログラミング言語はC, C++, Go, Pythonを中心として色々利用。現在は、Kaggle, 競プロなどをしながら悠々自適に活動中
Recommend
こちらの記事もどうぞ
記事URLをコピーしました